applikasjon

Integraler online på nettstedet for studenter og skoleelever for å konsolidere materialet de har dekket. Og trene dine praktiske ferdigheter. En komplett løsning av integraler online for deg i løpet av få øyeblikk vil hjelpe deg med å bestemme alle stadier av prosessen du anser integralet som en tabell. Ikke hver tabellintegral er tydelig synlig fra et gitt eksempel, noen ganger må du transformere den opprinnelige funksjonen for å finne antideriverten. I praksis kommer løsning av integraler ned på å tolke problemet med å finne originalen, det vil si antideriverte fra en uendelig familie av funksjoner, men hvis grensene for integrasjon er gitt, er det i henhold til Newton-Leibniz-formelen bare én enkelt funksjon igjen å bruke beregninger på. Online integraler - online ubestemt integral og online definite integral. Integralet til en funksjon på nett er summen av alle tall beregnet på integrering. Derfor, uformelt, er det online bestemte integralet området mellom grafen til funksjonen og x-aksen innenfor grensene for integrasjon. Eksempler på å løse problemer med integraler. La oss vurdere et komplekst integral over en variabel og relatere svaret til den videre løsningen av problemet. Det er mulig, som de sier, direkte å finne integralet til integranden. Enhver integral bestemmer med høy nøyaktighet området til figuren avgrenset av linjene. Dette er en av hans geometriske betydninger. Denne metoden gjør ting enklere for elevene. Flere trinn vil faktisk ikke ha stor innvirkning på vektoranalysen. Integralet til en funksjon på nett er det grunnleggende konseptet for integralregning Løse ubestemte integraler. I følge analysens hovedteorem er integrasjon den inverse operasjonen av differensiering, som hjelper til med å løse differensialligninger. Det er flere forskjellige definisjoner av driften av integrasjon, forskjellige i tekniske detaljer. Imidlertid er de alle kompatible, det vil si at to integrasjonsmetoder, hvis de kan brukes på en gitt funksjon, vil gi samme resultat. Det enkleste er Riemann-integralet - et bestemt integral eller et ubestemt integral. Uformelt kan integralet til en funksjon av én variabel introduseres som arealet under grafen (figuren som er innesluttet mellom grafen til funksjonen og x-aksen). Ethvert slikt delproblem kan rettferdiggjøre at beregning av integralet vil være ekstremt nødvendig helt i begynnelsen av en viktig tilnærming. Ikke glem dette! For å prøve å finne dette området, kan vi vurdere figurer som består av et visst antall vertikale rektangler, hvis base sammen danner et segment av integrering og oppnås ved å dele segmentet i passende antall små segmenter. Løse integraler online.. Integral online - ubestemt integral online og definitiv integral online. Løse integraler online: online ubestemt integral og online bestemt integral. Kalkulatoren løser integraler med en detaljert beskrivelse av handlingene og gratis! En online ubestemt integral for en funksjon er settet av alle antiderivater av en gitt funksjon. Hvis en funksjon er definert og kontinuerlig på et intervall, så er det for den antiderivative funksjon(eller familie av primitiver). Integralet definerer bare et uttrykk, vilkårene for det er satt av deg når et slikt behov oppstår. Det er bedre å nærme seg denne saken nøye og oppleve indre tilfredsstillelse fra arbeidet som er utført. Men å beregne integralet med en annen metode enn den klassiske fører noen ganger til uventede resultater, og man bør ikke bli overrasket over dette. Jeg er glad for at dette faktum vil ha en positiv resonans på det som skjer. Liste over bestemte integraler og ubestemte integraler av integraler med komplett detaljert trinnvis løsning. Alle integraler med detaljerte løsninger på nett. Ubestemt integral. Finner nr bestemt integral online er et veldig vanlig problem i høyere matematikk og andre tekniske områder av vitenskap. Grunnleggende metoder for integrering. Definisjon av integral, bestemt og ubestemt integral, tabell over integraler, Newton-Leibniz formel. Igjen kan du finne integralet ditt ved å bruke tabellen med integraluttrykk, men dette må fortsatt oppnås, siden ikke alt er så enkelt som det kan virke ved første øyekast. Tenk på ferdige bygg før feil blir funnet. Definitiv integral og metoder for beregning. Online bestemt integral med variabel øvre grense. Løse integraler online. Ethvert eksempel som vil hjelpe å beregne integralet ved hjelp av tabellformler vil være nyttig guide til handling for studenter på alle forberedelsesnivåer. Det viktigste steget mot riktig svar.. Integraler på nett. Ubestemte integraler som inneholder eksponentielle og logaritmiske funksjoner. Løse integraler online - du vil motta detaljert løsning Til forskjellige typer integraler: ubestemt, bestemt, upassende. Definite Integral Calculator beregner den definitive integralen online for en funksjon over et intervall ved hjelp av numerisk integrasjon. Integralet til en funksjon er en analog av summen av en sekvens. Uformelt sett er et bestemt integral arealet av en del av grafen til en funksjon. Løsning av integralet online.. Integral online - ubestemt integral online og definitiv integral online. Ofte bestemmer en slik integral hvor mye tyngre en kropp er enn en gjenstand med samme tetthet sammenlignet med den, og det spiller ingen rolle hvilken form det har, fordi overflaten ikke absorberer vann. Løse integraler online.. Integraler online - ubestemt integral online og bestemt integral online. Hver juniorstudent vet hvordan man finner integralet på nettet. På basen skolepensum denne delen av matematikk studeres også, men ikke i detalj, men bare det grunnleggende om et så komplekst og viktig emne. I de fleste tilfeller begynner studentene å studere integraler med omfattende teori, som også innledes med viktige emner, slik som den deriverte og passasje til grensen - de er også grenser. Å løse integraler begynner gradvis med de mest elementære eksemplene på enkle funksjoner, og slutter med bruken av mange tilnærminger og regler foreslått i forrige århundre og enda mye tidligere. Integralregning er for pedagogiske formål i lyceum og skoler, det vil si på videregående utdanningsinstitusjoner. Vår nettside vil alltid hjelpe deg og å løse integraler på nettet vil bli vanlig for deg, og viktigst av alt, en forståelig oppgave. Basert på denne ressursen kan du enkelt oppnå perfeksjon i denne matematiske delen. Ved å forstå reglene du studerer trinn for trinn, for eksempel integrering etter deler eller anvendelse av Chebyshev-metoden, kan du enkelt bestemme deg for maksimalt beløp poeng for enhver test. Så hvordan kan vi fortsatt beregne integralet, ved å bruke den velkjente tabellen over integraler, men på en slik måte at løsningen er riktig, korrekt og med et mest mulig nøyaktig svar? Hvordan lære dette og er det mulig for en vanlig førsteårsstudent å gjøre dette? så snart som mulig? La oss svare bekreftende på dette spørsmålet - du kan! Samtidig vil du ikke bare kunne løse et hvilket som helst eksempel, men også nå nivået til en høyt kvalifisert ingeniør. Hemmeligheten er enklere enn noen gang - du må gjøre maksimal innsats og bruke den nødvendige tiden til selvforberedelse. Dessverre er det ingen som har funnet på en annen måte ennå! Men ikke alt er så overskyet som det ser ut ved første øyekast. Hvis du kontakter tjenestenettstedet vårt med dette spørsmålet, vil vi gjøre livet ditt enklere, fordi nettstedet vårt kan beregne integraler online i detalj, med svært høy hastighet og et upåklagelig nøyaktig svar. I kjernen bestemmer ikke integralet hvordan forholdet mellom argumenter påvirker stabiliteten til systemet som helhet. Hvis bare alt var balansert. Sammen med hvordan du vil lære det grunnleggende om dette matematisk emne, kan tjenesten finne integralet til enhver integrand hvis dette integralet kan løses i elementære funksjoner. Ellers, for integraler som ikke er tatt i elementære funksjoner, er det i praksis ikke nødvendig å finne svaret i en analytisk eller, med andre ord, i en eksplisitt form. Alle beregninger av integraler kommer ned til å bestemme antiderivertefunksjonen til en gitt integrand. For å gjøre dette, beregne først ubestemt integral i henhold til alle lovene i matematikk på nettet. Bytt deretter om nødvendig de øvre og nedre verdiene til integralet. Hvis du ikke trenger å bestemme eller beregne numerisk verdi ubestemt integral, så legges en konstant til den resulterende antiderivative funksjonen, og definerer derved en familie av antiderivative funksjoner. Spesielt sted innen vitenskap og generelt innen ethvert ingeniørfelt, inkludert kontinuummekanikk, beskriver integrasjon hele mekaniske systemer, deres bevegelser og mye mer. I mange tilfeller bestemmer det sammensatte integralet bevegelsesloven materiell poeng. Det er et veldig viktig verktøy i studiet av anvendt vitenskap. Ut fra dette kan man ikke unngå å nevne storskalaberegninger for å bestemme eksistens- og adferdslovene mekaniske systemer. Kalkulator for å løse integraler online på nettsiden er et kraftig verktøy for profesjonelle ingeniører. Vi garanterer deg definitivt dette, men vi vil være i stand til å beregne integralet ditt først etter at du har lagt inn det riktige uttrykket i integrandens domene. Ikke vær redd for å gjøre feil, alt kan rettes i denne saken! Vanligvis kommer løsning av integraler ned på å bruke tabellfunksjoner fra kjente lærebøker eller leksikon. Som enhver annen ubestemt integral, vil den bli beregnet ved hjelp av standardformelen uten noen større kritikk. Førsteårsstudenter griper lett og naturlig stoffet de har studert på stedet, og for dem tar det noen ganger ikke mer enn to minutter å finne en integral. Og hvis en student har lært tabellen over integraler, kan han generelt bestemme svarene i hodet. Å utvide funksjoner med variabler i forhold til overflater betyr i utgangspunktet riktig vektorretning på et abscissepunkt. Den uforutsigbare oppførselen til overflatelinjer tar bestemte integraler som grunnlag i responskilden til matematiske funksjoner. Den venstre kanten av ballen berører ikke sylinderen som sirkelen er innskrevet i, hvis du ser på kuttet i et plan. Summen av små områder delt inn i hundrevis av stykkevis kontinuerlige funksjoner er online-integralet av gitt funksjon. Den mekaniske betydningen av integralet ligger i mange anvendte problemer, som å bestemme volumet av kropper og beregne massen til en kropp. Trippel- og dobbelintegraler er involvert i disse beregningene. Vi insisterer på at løsningen av integraler på nettet kun utføres under tilsyn av erfarne lærere og gjennom en rekke kontroller. Vi blir ofte spurt om ytelsen til studenter som ikke deltar på forelesninger, hopper over dem uten grunn, og hvordan de klarer å finne. selve integralen. Vi svarer at studenter er frie mennesker og er ganske i stand til å studere eksternt, forberede seg til en prøve eller eksamen i komforten av sitt eget hjem. I løpet av sekunder vil tjenesten vår hjelpe alle med å beregne integralet til en gitt funksjon over en variabel. Det oppnådde resultatet bør kontrolleres ved å ta derivatet av antiderivatfunksjonen. I dette tilfellet blir konstanten fra løsningen av integralet null. Denne regelen gjelder selvsagt for alle. Ettersom flerretningsoperasjoner er rettferdiggjort, reduseres det ubestemte integralet ofte til å dele domenet i små deler. Noen elever og skoleelever forsømmer imidlertid dette kravet. Som alltid kan online integraler løses i detalj av tjenestenettstedet vårt og det er ingen begrensninger på antall forespørsler, alt er gratis og tilgjengelig for alle. Det er ikke mange nettsteder som gir et trinn-for-steg-svar i løpet av sekunder, og viktigst av alt med høy nøyaktighet og i en praktisk form. I det siste eksemplet på side fem hjemmelekser Jeg kom over en som indikerer behovet for å beregne integralen trinn for trinn. Men vi må ikke glemme hvordan det er mulig å finne integralet ved hjelp av en ferdig tjeneste, tidstestet og testet på tusenvis av løste eksempler på nett. Hvordan et slikt integral bestemmer bevegelsen til systemet er klart og tydelig demonstrert for oss av arten av bevegelsen til den viskøse væsken, som er beskrevet av dette ligningssystemet.

Å løse integraler er en enkel oppgave, men bare for noen få utvalgte. Denne artikkelen er for de som ønsker å lære å forstå integraler, men vet ingenting eller nesten ingenting om dem. Integral... Hvorfor er det nødvendig? Hvordan beregne det? Hva er bestemte og ubestemte integraler? Hvis den eneste bruken du vet om for en integral er å bruke en heklenål formet som et integrert ikon for å få noe nyttig ut av vanskelig tilgjengelige steder, så velkommen! Finn ut hvordan du løser integraler og hvorfor du ikke kan klare deg uten dem.

Vi studerer konseptet "integral"

Integrasjon var kjent tilbake i Det gamle Egypt. Selvfølgelig ikke inne moderne form, men fortsatt. Siden den gang har matematikere skrevet mange bøker om dette emnet. Spesielt utmerket seg Newton Og Leibniz , men essensen av ting har ikke endret seg. Hvordan forstå integraler fra bunnen av? Aldri! For å forstå dette emnet trenger du fortsatt grunnleggende kunnskap grunnleggende matematisk analyse. Det er denne grunnleggende informasjonen du finner på bloggen vår.

Ubestemt integral

La oss ha en funksjon f(x) .

Ubestemt integrert funksjon f(x) denne funksjonen kalles F(x) , hvis deriverte er lik funksjonen f(x) .

Med andre ord, en integral er en derivat i revers eller en antiderivat. Les forresten om hvordan i artikkelen vår.

En antiderivativ eksisterer for alle kontinuerlige funksjoner. Også et konstant tegn legges ofte til antiderivatet, siden derivatene av funksjoner som avviker med en konstant sammenfaller. Prosessen med å finne integralet kalles integrasjon.

Enkelt eksempel:

For ikke å hele tiden beregne antiderivater av elementære funksjoner, er det praktisk å sette dem i en tabell og bruke ferdige verdier:

Sikker integral

Når vi har å gjøre med begrepet et integral, har vi å gjøre med uendelig små mengder. Integralet vil bidra til å beregne arealet av figuren, massen til den inhomogene kroppen, avstanden tilbakelagt ved ujevn bevegelse sti og mye mer. Det bør huskes at et integral er summen av et uendelig stort antall infinitesimale ledd.

Tenk deg som et eksempel en graf av en funksjon. Hvordan finne arealet til en figur, begrenset av tidsplanen funksjoner?

Ved hjelp av en integral! La oss dele den kurvelinjeformede trapesen, begrenset av koordinataksene og grafen til funksjonen, i uendelig små segmenter. På denne måten vil figuren deles inn i tynne kolonner. Summen av arealene til kolonnene vil være arealet av trapesen. Men husk at en slik beregning vil gi et omtrentlig resultat. Men jo mindre og smalere segmentene er, jo mer nøyaktig blir beregningen. Hvis vi reduserer dem i en slik grad at lengden har en tendens til null, vil summen av arealene til segmentene tendere til området til figuren. Dette er en bestemt integral, som er skrevet slik:

Punktene a og b kalles integrasjonsgrenser.

Bari Alibasov og gruppen "Integral"

Forresten! For våre lesere er det nå 10% rabatt på

Regler for beregning av integraler for dummies

Egenskaper til det ubestemte integralet

Hvordan løser man et ubestemt integral? Her skal vi se på egenskapene til det ubestemte integralet, noe som vil være nyttig når du skal løse eksempler.

• Den deriverte av integralet er lik integranden:

• Konstanten kan tas ut under integrertegnet:

• Integral av summen lik summen integraler. Dette gjelder også for forskjellen:

Egenskaper til en bestemt integral

• Linearitet:

• Tegnet på integralet endres hvis grensene for integrasjon byttes:

• På noen poeng en, b Og Med:

Vi har allerede funnet ut at et bestemt integral er grensen for en sum. Men hvordan få en bestemt verdi når man løser et eksempel? For dette er det Newton-Leibniz-formelen:

Eksempler på løsning av integraler

Nedenfor skal vi vurdere flere eksempler på å finne ubestemte integraler. Vi inviterer deg til å finne ut detaljene ved løsningen selv, og hvis noe er uklart, still spørsmål i kommentarene.

For å forsterke materialet, se en video om hvordan integraler løses i praksis. Fortvil ikke hvis integralen ikke gis med en gang. Spør og de vil fortelle deg alt de vet om beregning av integraler. Med vår hjelp vil enhver trippel eller buet integral over en lukket overflate være innenfor din makt.

Finne ubestemt integral(sett med antiderivater eller "antiderivater") betyr å rekonstruere en funksjon fra et kjent derivat av denne funksjonen. Restaurert sett med antiderivater F(x) + MED for funksjon f(x) tar hensyn til integrasjonskonstanten C. Basert på bevegelseshastigheten til et materiell punkt (derivert), kan bevegelsesloven til dette punktet (antiderivativ) gjenopprettes; i henhold til akselerasjonen av et punkts bevegelse - dets hastighet og bevegelsesloven. Som du kan se, er integrering et bredt felt for aktivitetene til fysikkens Sherlock Holmeses. Og i økonomi er mange konsepter representert gjennom funksjoner og deres derivater, og derfor er det for eksempel mulig å gjenopprette volumet av produkter produsert på tilsvarende tidspunkt ved å bruke arbeidsproduktivitet på et bestemt tidspunkt (derivat).

For å finne det ubestemte integralet må det ganske mye til et stort nummer av grunnleggende integrasjonsformler. Men prosessen med å finne det er mye vanskeligere enn bare å bruke disse formlene. All kompleksiteten er ikke knyttet til integrasjon, men til å bringe det integrerbare uttrykket til en form som gjør det mulig å finne det ubestemte integralet ved hjelp av grunnformlene nevnt ovenfor. Dette betyr at for å begynne praksisen med integrering, må du aktivere det du har lært i videregående skole ferdigheter for å transformere uttrykk.

Vi skal lære å finne integraler ved hjelp av egenskaper og tabell over ubestemte integraler fra en leksjon om de grunnleggende begrepene i dette emnet (åpnes i et nytt vindu).

Det finnes flere metoder for å finne integralet, hvorav variabel erstatningsmetode Og integrasjon etter delemetode- et obligatorisk herresett for alle som har bestått høyere matematikk. Det er imidlertid mer nyttig og morsomt å begynne å mestre integrasjon ved å bruke utvidelsesmetoden, basert på følgende to teoremer om egenskapene til det ubestemte integralet, som vi gjentar her for enkelhets skyld.

Teorem 3. Konstantfaktoren i integranden kan tas ut av tegnet til det ubestemte integralet, dvs.

Teorem 4. Det ubestemte integralet av en algebraisk sum av et endelig antall funksjoner er lik algebraisk sum ubestemte integraler av disse funksjonene, dvs.

(2)

I tillegg kan følgende regel være nyttig i integrasjon: hvis uttrykket av integranden inneholder en konstant faktor, multipliseres uttrykket av antideriverten med inversen av konstantfaktoren, dvs.

(3)

Siden dette er en introduksjonsleksjon for å løse integreringsproblemer, er det viktig å merke seg to ting som enten helt i begynnelsen eller litt senere kan overraske deg. Overraskelsen skyldes det faktum at integrasjon er den inverse operasjonen av differensiering og det ubestemte integralet med rette kan kalles "antiderivatet".

Det første du ikke bør bli overrasket over når du integrerer. I tabellen over integraler det er formler som ikke har noen analoger blant de deriverte tabellformlene . Dette er følgende formler:

Du kan imidlertid sørge for at de deriverte av uttrykkene på høyresiden av disse formlene faller sammen med de tilsvarende integrandene.

Den andre tingen som ikke burde være overraskende ved integrering. Selv om den deriverte av enhver elementær funksjon også er en elementær funksjon, ubestemte integraler av noen elementære funksjoner er ikke lenger elementære funksjoner . Eksempler på slike integraler kan være følgende:

For å utvikle integrasjonsteknikker vil følgende ferdigheter være nyttige: å redusere brøker, dele et polynom i telleren av en brøk med et monom i nevneren (for å få summen av ubestemte integraler), konvertere røtter til potenser, multiplisere et monom med en polynom, heve til en potens. Disse ferdighetene er nødvendige for transformasjoner av integranden, som skal resultere i summen av integralene som er tilstede i tabellen over integraler.

Å finne ubestemte integraler sammen

Eksempel 1. Finn det ubestemte integralet

.

Løsning. Vi ser i nevneren til integranden et polynom der x er kvadratisk. Dette er et nesten sikkert tegn på at du kan bruke tabellintegral 21 (med en arctangent som resultat). Vi tar ut faktor-to fra nevneren (det er en slik egenskap ved integralet - konstantfaktoren kan tas ut utover fortegnet til integralet; den ble nevnt ovenfor som setning 3). Resultatet av alt dette:

Nå er nevneren summen av kvadrater, som betyr at vi kan bruke den nevnte tabellintegralen. Til slutt får vi svaret:

.

Eksempel 2. Finn det ubestemte integralet

Løsning. Vi bruker igjen teorem 3 - egenskapen til integralet, på grunnlag av hvilken den konstante faktoren kan tas ut av tegnet til integralet:

Vi bruker formel 7 fra tabellen over integraler (variabel til potens) på integrandfunksjonen:

.

Vi reduserer de resulterende brøkene og vi har det endelige svaret:

Eksempel 3. Finn det ubestemte integralet

Løsning. Ved å bruke først teorem 4 og deretter teorem 3 på egenskaper, finner vi dette integralet som summen av tre integraler:

Alle tre oppnådde integraler er tabellformede. Vi bruker formel (7) fra tabellen over integraler for n = 1/2, n= 2 og n= 1/5, og deretter

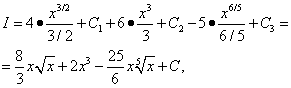
kombinerer alle de tre vilkårlige konstantene som ble introdusert da de tre integralene ble funnet. I lignende situasjoner bør derfor bare én vilkårlig integrasjonskonstant introduseres.

Eksempel 4. Finn det ubestemte integralet

Løsning. Når nevneren til integranden inneholder en monomial, kan vi dele telleren med nevneren ledd for ledd. Det opprinnelige integralet ble til summen av to integraler:

.

For å bruke tabellintegralen transformerer vi røttene til potenser og her er det endelige svaret:

Vi fortsetter å finne ubestemte integraler sammen

Eksempel 7. Finn det ubestemte integralet

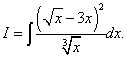
Løsning. Hvis vi transformerer integranden ved å kvadrere binomialet og dele telleren med nevneren ledd for ledd, så blir det opprinnelige integralet summen av tre integraler.

Ubestemt integral.
Detaljerte eksempler løsninger

I denne leksjonen vil vi begynne å studere emnet Ubestemt integral, og vi vil også analysere i detalj eksempler på løsninger på de enkleste (og ikke så enkle) integralene. I denne artikkelen vil jeg begrense meg til et minimum av teori, og nå er vår oppgave å lære å løse integraler.

Hva trenger du å vite for å mestre materialet? For å takle integralregning, må du være i stand til å finne derivater, på et minimum, på et mellomnivå. Derfor, hvis materialet er lansert, anbefaler jeg at du først leser leksjonene nøye Hvordan finne den deriverte? Og Derivat av en kompleks funksjon. Det vil ikke være bortkastet erfaring hvis du har flere dusin (helst hundre) uavhengig funnet derivater under beltet. I det minste bør du ikke bli forvirret av oppgaver for å skille mellom de enkleste og vanligste funksjonene. Det ser ut til, hva har derivater med det å gjøre hvis artikkelen handler om integraler?! Her er greia. Faktum er at det å finne deriverte og å finne ubestemte integraler (differensiering og integrasjon) er to gjensidig inverse handlinger, som addisjon/subtraksjon eller multiplikasjon/divisjon. Dermed, uten ferdigheten (+ litt erfaring) med å finne derivater, kan du dessverre ikke komme videre.

I denne forbindelse trenger vi følgende undervisningsmateriell: Derivattabell Og Tabell over integraler. Referansemanualer kan åpnes, lastes ned eller skrives ut på siden Matematiske formler og tabeller.

Hva er vanskeligheten med å lære ubestemte integraler? Hvis det i derivater er strengt 5 regler for differensiering, en tabell med derivater og en ganske klar algoritme for handlinger, så er alt annerledes i integraler. Det finnes dusinvis av integreringsmetoder og teknikker. Og hvis integreringsmetoden i utgangspunktet er valgt feil (dvs. du vet ikke hvordan du skal løse), kan integralet "prikkes" bokstavelig talt i flere dager, som et ekte puslespill, for å prøve å oppdage forskjellige teknikker og triks. Noen mennesker liker det til og med. Forresten, dette er ikke en spøk, jeg hørte ganske ofte fra studenter en mening som "Jeg har aldri hatt noen interesse for å løse en grense eller derivat, men integraler er en helt annen sak, det er fascinerende, det er alltid et ønske om å "hack" en kompleks integral." Stoppe. Nok av den svarte humoren, la oss gå videre til disse svært ubestemte integralene.

Siden det er så mange måter å løse det på, hvor skal man da begynne å studere ubestemte integraler for en tekanne? I integralregning er det etter min mening tre søyler eller en slags "akse" som alt annet dreier seg om. Først av alt bør du ha en god forståelse av de enkleste integralene (denne artikkelen). Deretter må du jobbe gjennom leksjonen i detalj. DETTE DEN VIKTIGSTE TEKNIKK! Kanskje til og med den viktigste artikkelen av alle artiklene mine om integraler. Og for det tredje bør du definitivt gjøre deg kjent med metoden for integrering av deler, siden den kan brukes til å integrere en lang rekke funksjoner. Hvis du mestrer minst disse tre leksjonene, vil du ikke lenger ha to. Du kan bli tilgitt for at du ikke kjenner integraler fra trigonometriske funksjoner, integraler fra brøker, integraler fra brøk-rasjonelle funksjoner, integraler fra irrasjonelle funksjoner (røtter), men hvis du blir sittende fast på erstatningsmetoden eller metoden for integrering med deler, så vil være veldig, veldig dårlig.

Demotivatorer er nå veldig vanlig på RuNet. I sammenheng med å studere integraler, tvert imot, er det rett og slett nødvendig MOTIVATOR. Som i den vitsen om Vasily Ivanovich, som motiverte både Petka og Anka. Kjære late folk, frilastere og andre vanlige studenter, les følgende. Kunnskap og ferdigheter om det ubestemte integralet vil være nødvendig i videre studier, spesielt når man studerer det bestemte integralet, upassende integraler og differensialligninger i det andre året. Behovet for å ta integralet oppstår selv i sannsynlighetsteori! Dermed, uten integraler BLIR VIRKELIG STENGT VEI til sommerøkt og 2. år. Jeg er seriøs. Konklusjonen er denne. Jo flere integraler forskjellige typer du bestemmer, jo lettere blir det fremtidig liv . Ja, det vil ta ganske mye tid, ja, noen ganger vil du ikke, ja, noen ganger "til helvete med det, med denne integralen, kanskje du ikke får det." Men neste tanke bør inspirere og varme sjelen din vil lønne seg fullt ut! Du vil være i stand til å knekke differensialligninger som nøtter og enkelt håndtere integraler som du vil møte i andre deler av høyere matematikk. Etter å ha grundig forstått den ubestemte integralen, VIL DU FAKTISK MESTRE EN FLERE DELER AV TÅRNET.

Og så jeg kunne bare ikke la være å skape intensivt kurs på integrasjonsteknikken, som viste seg å være overraskende kort - de som ønsker det kan bruke pdf-boken og forberede seg VELDIG raskt. Men materialene på siden er på ingen måte dårligere!

Så la oss starte enkelt. La oss se på tabellen over integraler. Som med derivater, legger vi merke til flere integreringsregler og en tabell med integraler av noen elementære funksjoner. Det er lett å se at enhver tabellintegral (og faktisk ethvert ubestemt integral) har formen:

La oss umiddelbart forstå notasjonene og begrepene:

– integrert ikon.

– integrand-funksjon (skrevet med bokstaven "s").

– differensialikon. Når du skriver integralet og under løsningen, er det viktig å ikke miste dette ikonet. Det vil være en merkbar feil.

– integrant uttrykk eller "fylling" av integralet.

– antiderivative funksjon.

– mange originale funksjoner. Det er ikke nødvendig å være tungt lastet med termer, det viktigste er at i enhver ubestemt integral legges en konstant til svaret.

Å løse en integral betyr å finne en bestemt funksjon ved å bruke noen regler, teknikker og en tabell.

La oss se på oppføringen igjen:

La oss se på tabellen over integraler.

Hva skjer? Vi har de venstre delene bli til til andre funksjoner: .

La oss forenkle vår definisjon.

Å løse en ubestemt integral betyr å konvertere den til en bestemt funksjon ved å bruke noen regler, teknikker og en tabell.

Ta for eksempel tabellintegralen . Hva skjedde? omgjort til en funksjon.

Som i tilfellet med derivater, for å lære å finne integraler, trenger du ikke å være klar over hva er en integral, en antiderivert funksjon fra et teoretisk synspunkt. Det er nok å bare utføre transformasjoner i henhold til noen formelle regler. Så i tilfelle Det er slett ikke nødvendig å forstå hvorfor integralet blir til . Foreløpig kan vi ta denne og andre formler for gitt. Alle bruker strøm, men de færreste tenker på hvordan elektroner beveger seg gjennom ledninger.

Siden differensiering og integrasjon er motsatte operasjoner, så for alle antiderivater som finnes Ikke sant, følgende er sant:

Med andre ord, hvis du skiller riktig svar, må du få den opprinnelige integrandfunksjonen.

La oss gå tilbake til den samme tabellintegralen .

La oss bekrefte gyldigheten av denne formelen. Vi tar den deriverte av høyresiden:

er den opprinnelige integrand-funksjonen.

Det har forresten blitt tydeligere hvorfor en konstant alltid tilordnes en funksjon. Ved differensiert blir konstanten alltid til null.

Løs ubestemt integral- det betyr å finne en haug med alle antiderivater, og ikke bare én funksjon. I tabelleksemplet under vurdering, , , , osv. – alle disse funksjonene er løsninger på integralet. Det er uendelig mange løsninger, så vi skriver det kort ned:

Dermed er ethvert ubestemt integral ganske enkelt å sjekke (i motsetning til derivater, hvor en god sjekk bare kan gjøres ved å bruke matematiske programmer). Dette er en viss kompensasjon for et stort antall integraler av forskjellige typer.

La oss gå videre til å vurdere spesifikke eksempler. La oss begynne, som når vi studerer den deriverte,
med to regler for integrering, også kalt linearitetsegenskaper ubestemt integral:

– konstantfaktoren kan (og bør) tas ut av integrertegnet.

– integralet av den algebraiske summen av to funksjoner er lik den algebraiske summen av to integraler av hver funksjon separat. Denne eiendommen gyldig for et hvilket som helst antall vilkår.

Som du ser er reglene i utgangspunktet de samme som for derivater.

Eksempel 1

Løsning: Det er mer praktisk å skrive det om på papir.

(1) Bruk regelen . Ikke glem å skrive ned differensialsymbolet under hver integral. Hvorfor under hver? - Dette er en full multiplikator, hvis vi beskriver løsningen i detalj, bør det første trinnet skrives slik:

(2) Etter regelen , tar vi alle konstantene utenfor integrertegnet. Vær oppmerksom på at siste termin er en konstant, vi tar den også ut.
I tillegg forbereder vi på dette trinnet røtter og krefter for integrering. På samme måte som ved differensiering må røttene representeres i formen . Flytt røttene og potensene som er plassert i nevneren oppover.

! Merk: i motsetning til derivater, bør røtter i integraler ikke alltid reduseres til formen , men grader skal overføres oppover. For eksempel er dette en ferdig bordintegral, og alle slags kinesiske triks som helt unødvendig. Tilsvarende: – også et tabellintegral, det er ingen vits i å representere brøken i formen . Studer tabellen nøye!

(3) Alle våre integraler er tabellformede. Vi utfører transformasjonen ved å bruke en tabell ved å bruke formlene: , Og .
Spesiell oppmerksomhet Jeg viser til integrasjonsformelen strømfunksjon , det forekommer veldig ofte, det er bedre å huske det. Det skal bemerkes at tabellintegralen er spesielt tilfelle samme formel: .
Det er nok å legge til konstanten én gang på slutten av uttrykket (og ikke sette dem etter hver integral).
(4) Vi skriver resultatet oppnådd i en mer kompakt form, alle potenser i formen er igjen representert som røtter, potenser med negativ eksponent tilbakestilles til nevneren.

Undersøkelse. For å utføre kontrollen må du skille mellom det mottatte svaret:

Fikk originalen integrand, som betyr at integralet ble funnet riktig. Det de danset fra er det de kom tilbake til. Du vet, det er veldig bra når en historie med en integral ender på denne måten.

Fra tid til annen er det en litt annen tilnærming til å kontrollere det ubestemte integralet, ikke den deriverte er hentet fra svaret, men differensialen:

De som forsto fra første semester forsto, men det som er viktig for oss er ikke de teoretiske finessene, men det som er viktig er hva vi skal gjøre videre med denne differensialen. Det må avsløres, og fra et formelt teknisk synspunkt er dette nesten det samme som å finne et derivat. Differensialet avsløres som følger: vi fjerner ikonet, legger et slag til høyre over parentesen og legger til en faktor på slutten av uttrykket:

Mottatt original integrand, som betyr at integralet ble funnet riktig.

Jeg liker den andre metoden for å sjekke mindre, siden jeg i tillegg må tegne store parenteser og dra differensialikonet til slutten av sjekken. Selv om det er mer korrekt eller "mer respektabelt" eller noe.

Faktisk kunne jeg ha vært taus om den andre bekreftelsesmetoden helt. Poenget ligger ikke i metoden, men i at vi har lært å åpne differensialen. En gang til.

Differansen avsløres som følger:

1) fjern ikonet;
2) til høyre over braketten setter vi et slag (betegnelse av derivatet);
3) på slutten av uttrykket tildeler vi en faktor .

For eksempel:

Husk dette. Vi vil trenge denne teknikken veldig snart.

Eksempel 2

Finn det ubestemte integralet. Utfør sjekk.

Når vi finner en ubestemt integral, prøver vi ALLTID å sjekke Dessuten er det en stor mulighet for dette. Ikke alle typer problemer i høyere matematikk er en gave fra dette synspunktet. Det spiller ingen rolle så ofte testoppgaver ingen verifisering er nødvendig, ingen sjekker den, og ingenting hindrer den i å utføres på et utkast. Et unntak kan bare gjøres når det ikke er nok tid (for eksempel under en prøve eller eksamen). Personlig sjekker jeg alltid integraler, og jeg anser mangelen på kontroll som en hack-jobb og en dårlig utført oppgave.

Eksempel 3

Finn det ubestemte integralet. Utfør sjekk.

Løsning: Ved å analysere integralet ser vi at vi har produktet av to funksjoner, og til og med eksponentiseringen av et helt uttrykk. Dessverre, innen integrert kamp er det ingen gode og praktiske formler for å integrere produktet og det spesielle , .

Og derfor, når et produkt eller en kvotient er gitt, er det alltid fornuftig å se om det er mulig å transformere integranden til en sum?

Eksemplet som vurderes er tilfellet når det er mulig. Først vil jeg gi den komplette løsningen, kommentarer vil være nedenfor.

(1) Vi bruker den gode gamle formelen for kvadratet av summen, for å bli kvitt graden.

(2) Vi setter den i parentes og blir kvitt produktet.

Eksempel 4

Finn det ubestemte integralet. Utfør sjekk.

Dette er et eksempel for deg å løse selv. Svaret og fullstendig løsning er på slutten av leksjonen.

Eksempel 5

Finn det ubestemte integralet. Utfør sjekk.

I i dette eksemplet integranden er en brøkdel. Når vi ser en brøk i integranden, bør den første tanken være spørsmålet: Er det mulig på en eller annen måte å bli kvitt denne brøken, eller i det minste forenkle den?

Vi legger merke til at nevneren inneholder en enkelt rot av "X". En i feltet er ikke en kriger, noe som betyr at vi kan dele telleren med nevneren begrep for begrep:

Handlinger med brøkkrefter Jeg kommenterer ikke, siden de har blitt diskutert gjentatte ganger i artikler om derivatfunksjonen. Hvis du fortsatt er forvirret over et eksempel som , og du fortsatt ikke kan få det riktige svaret, anbefaler jeg at du går til skolebøkene. I høyere matematikk møter man brøker og operasjoner med dem ved hvert trinn.

Merk også at løsningen mangler ett trinn, nemlig å anvende reglene , . Vanligvis, selv under den første erfaringen med å løse integraler, blir disse egenskapene tatt for gitt og blir ikke beskrevet i detalj.

Eksempel 6

Finn det ubestemte integralet. Utfør sjekk.

Dette er et eksempel for deg å løse selv. Svaret og fullstendig løsning er på slutten av leksjonen.

Generelt er ting ikke så enkelt med brøker i integraler, tilleggsmateriale om integrering av brøker av noen typer finnes i artikkelen Integrering av noen brøker.

! Men før du går videre til artikkelen ovenfor, må du gjøre deg kjent med leksjonen Substitusjonsmetode i ubestemt integral. Poenget er at å subsumere en funksjon under en differensiell eller variabel erstatningsmetode er sentralt punkt i studiet av emnet, siden det ikke bare finnes "i rene oppgaver på erstatningsmetoden", men også i mange andre typer integraler.

Jeg ønsket virkelig å inkludere noen flere eksempler denne leksjonen, men jeg sitter her nå, skriver denne teksten på Verde og merker at artikkelen allerede har vokst til en anstendig størrelse.
Og derfor introduksjonskurs integraler for dummies har kommet til en slutt.

Jeg ønsker deg suksess!

Løsninger og svar:

Eksempel 2: Løsning:

Eksempel 4: Løsning:

I dette eksemplet brukte vi den forkortede multiplikasjonsformelen

Eksempel 6: Løsning:

Jeg fullførte sjekken, og du? ;)