Chi ha creato la sezione aurea. Proporzioni auree in letteratura

Candidato di scienze tecniche V. BELYANIN, ricercatore leader presso il Centro di ricerca russo "Kurchatov Institute", E. ROMANOVA, studentessa presso MADI (GTU)

Scienza e vita // Illustrazioni

La sezione aurea non viene insegnata a scuola. E quando uno degli autori dell'articolo proposto di seguito (candidato di scienze tecniche V. Belyanin) ha parlato della sezione aurea a un richiedente che stava progettando di entrare in MADI, nel processo di preparazione agli esami presso l'istituto, il problema è sorto inaspettatamente vivo interesse e molte domande, alle quali è stata data risposta “sul posto”. Abbiamo deciso di cercarli insieme e poi sono state scoperte sottigliezze nella sezione aurea che in precedenza erano sfuggite ai ricercatori. La creatività congiunta ha portato a un lavoro che conferma ancora una volta le capacità creative dei giovani e dà speranza che il linguaggio della scienza non vada perduto.

Gli schemi della matematica, come quelli di un artista o quelli di un poeta, devono essere belli; Le idee, come i colori o le parole, devono essere combinate armoniosamente. La bellezza è il primo criterio: non c’è posto al mondo per la matematica brutta.
JH Hardy

bellezza problema matematico costituisce uno degli incentivi più importanti per il suo sviluppo infinito e la ragione per la generazione di numerose applicazioni. A volte passano decine, centinaia e talvolta migliaia di anni, ma le persone trovano ancora e ancora colpi di scena inaspettati in una soluzione ben nota e nella sua interpretazione. Uno di questi problemi longevi e affascinanti si è rivelato essere il problema della sezione aurea (GR), che riflette gli elementi di grazia e armonia del mondo che ci circonda. Vale la pena ricordare, a proposito, che sebbene la proporzione stessa fosse nota a Euclide, il termine “sezione aurea” fu introdotto da Leonardo da Vinci (vedi “Scienza e vita”).

Dal punto di vista geometrico, la sezione aurea implica la divisione di un segmento in due parti disuguali in modo che la parte più grande sia la media proporzionale tra l'intero segmento e la parte più piccola (Fig. 1).

Algebricamente ciò si esprime nel modo seguente:

Lo studio di questa proporzione ancor prima della sua soluzione mostra quella tra i segmenti UN E B Ci sono almeno due relazioni sorprendenti. Ad esempio dalla proporzione (1) si ottiene facilmente l'espressione

che imposta la proporzione tra i segmenti UN, B, la loro differenza e somma. Pertanto, possiamo dire diversamente della sezione aurea: due segmenti sono in una relazione armoniosa se la loro differenza si riferisce al segmento più piccolo come il segmento più grande si riferisce alla loro somma.

La seconda relazione si ottiene se il segmento originale viene preso uguale a uno: UN + B= 1, che è molto spesso usato in matematica. In questo caso

UN 2 - B 2 = UN - B = ab.

Da questi risultati conseguono due sorprendenti relazioni tra i segmenti UN E B:

UN 2 - B 2 = UN - B = ab,(2)

che verrà utilizzato in futuro.

Passiamo ora alla risoluzione della proporzione (1). In pratica si utilizzano due possibilità.

1. Indichiamo la relazione UN/B Attraverso. Quindi otteniamo l'equazione

X 2 - X - 1 = 0, (3)

Di solito viene considerata solo la radice positiva X 1, dando una divisione semplice e visiva di un segmento in una data proporzione. Infatti, se prendiamo l'intero segmento come uno, allora utilizzeremo il valore di questa radice X 1, otteniamo UN ≈ 0,618,B≈ 0,382.

È la radice positiva X 1 dell'equazione (3) viene spesso chiamato rapporto aureo O proporzione della sezione aurea. Si chiama la corrispondente divisione geometrica di un segmento rapporto aureo(punto CON nella fig. 1).

Per comodità di ulteriore presentazione, indichiamo X 1 = D. Non esiste ancora una designazione generalmente accettata per la sezione aurea. Ciò è apparentemente dovuto al fatto che a volte viene inteso come un altro numero, di cui parleremo di seguito.

La radice negativa, lasciata come al solito da parte X 2 porta ad una divisione meno netta del segmento in due parti disuguali. Il punto è che fornisce un punto di divisione CON, che si trova al di fuori del segmento (la cosiddetta divisione esterna). Infatti, se UN + B= 1, quindi utilizzando la radice X 2, otteniamo UN ≈ -1,618, B≈ 2.618. Quindi il segmento UN deve essere posato in senso negativo (Fig. 2).

2. La seconda opzione per risolvere la proporzione (1) non è fondamentalmente diversa dalla prima. Assumiamo relazione sconosciuta B/UN e denotarlo con sì. Quindi otteniamo l'equazione

sì 2 + sì -1 = 0 , (4)

che ha radici irrazionali

Se UN + B= 1, quindi utilizzando la radice sì 1, otteniamo UN = sì 1 ≈ 0,618, B≈ 0,382. Per la radice sì 2 otteniamo UN ≈ -1,618, B≈ 2.618. Divisione geometrica di un segmento in proporzione alla sezione aurea utilizzando le radici sì 1 e sì 2 è del tutto identico alla versione precedente e corrisponde alla Fig. 1 e 2.

Radice positiva sì 1 fornisce direttamente la soluzione desiderata al problema e viene anche chiamato rapporto aureo .

Per comodità indichiamo il valore della radice sì 1 = D.

Pertanto, in letteratura, la proporzione aurea è espressa matematicamente dal numero D 1.618 o numero D 0,618, tra i quali esistono due rapporti sorprendenti:

Ggg= 1 e D - D = 1. (5)

È stato dimostrato che non esiste altra coppia di numeri simili che abbia queste proprietà.

Usando entrambe le notazioni per la proporzione aurea, scriviamo le soluzioni delle equazioni (3) e (4) in forma simmetrica: = D, = -D, = D, = -D.

Le proprietà insolite della sezione aurea sono descritte in modo sufficientemente dettagliato in letteratura. Sono così sorprendenti che hanno affascinato le menti di molti pensatori eccezionali e hanno creato un'aura di mistero attorno a loro.

La proporzione aurea si trova nella configurazione delle piante e dei minerali, nella struttura di parti dell'Universo e nella scala musicale. Riflette i principi globali della natura, permeando tutti i livelli di organizzazione degli oggetti viventi e inanimati. Viene utilizzato in architettura, scultura, pittura, scienza, informatica e nella progettazione di articoli per la casa. Le creazioni che portano la configurazione della sezione aurea appaiono proporzionate e coerenti, sono sempre piacevoli alla vista, e il linguaggio matematico La proporzione aurea non è meno aggraziata ed elegante.

Oltre alle uguaglianze (5) dalla relazione (2), possiamo distinguere tre relazioni interessanti che hanno una certa perfezione e sembrano piuttosto attraenti ed esteticamente gradevoli:

(6)

La grandiosità e la profondità della natura possono essere percepite non solo, ad esempio, contemplando le stelle o le cime delle montagne, ma anche scrutando alcune formule sorprendenti, molto apprezzate dai matematici per la loro bellezza. Questi includono gli eleganti rapporti della proporzione aurea, la fantastica formula di Eulero e iπ = -1 (dove io= √-1), la formula che definisce il famoso numero di Napier (la base dei logaritmi naturali): e = lim(1 + 1/ N) n = 2.718 a N→ ∞ e molti altri.

Dopo aver risolto la proporzione (1), la sua idea sembra abbastanza semplice, ma, come spesso accade con molte persone, a prima vista compiti semplici, ci sono molte sottigliezze nascoste in esso. Una di queste notevoli sottigliezze, che i ricercatori finora hanno trascurato, è la connessione tra le radici delle equazioni (3) e (4) con gli angoli di tre meravigliosi triangoli.

Per vederlo, considera come un segmento di linea unidimensionale, diviso nella proporzione della sezione aurea, può essere facilmente trasformato in un'immagine bidimensionale sotto forma di triangolo. Per fare ciò, utilizzando prima la Fig. 1, mettere da parte sul segmento AB lunghezza del segmento UN due volte - dal punto UN verso il punto IN e, viceversa, dal punto IN di fianco UN. Otteniamo due punti CON 1 e CON 2 dividendo il segmento AB da estremità diverse in proporzione alla sezione aurea (Fig. 3). Conteggio di segmenti uguali AC 1 e Sole 2 raggi e i punti UN E IN centri dei cerchi, disegna due archi finché non si intersecano nel punto più alto CON. Collegare i punti UN E CON, E IN E CON, otteniamo un triangolo isoscele ABC con i partiti AB = UN + B = 1, AC = = sole = UN = D≈ 0,618. La dimensione degli angoli ai vertici UN E IN indichiamo α, al vertice CON-β. Calcoliamo questi angoli.

Per il teorema del coseno

(AB) 2 = 2(AC) 2 (1 - cos β).

Sostituendo i valori numerici dei segmenti AB E AC in questa formula, otteniamo

Allo stesso modo otteniamo

(8)

L'emergere della proporzione aurea in un'immagine bidimensionale ha permesso di collegare le radici delle equazioni (3) e (4) con gli angoli di un triangolo ABC, che può essere chiamato il primo triangolo della sezione aurea.

Eseguiamo una costruzione simile utilizzando la Fig. 2. Se sulla continuazione del segmento AB rinviare dal punto IN a destra un segmento di dimensioni uguali al segmento UN e ruotare attorno ai centri UN E IN su entrambi i segmenti come raggi finché non si toccano, otteniamo secondo triangolo rapporto aureo(Fig. 4) . In questo triangolo isoscele, il lato AB = UN + B= 1, lato AC = Sole = D≈1.618, e quindi, utilizzando la formula del teorema del coseno, otteniamo

(9)

Angolo a al vertice CONè uguale a 36 o ed è legato alla proporzione aurea dalla relazione (8). Come nel caso precedente, gli angoli di questo triangolo sono legati alle radici delle equazioni (3) e (4).

Il secondo triangolo della proporzione aurea funge da elemento costitutivo principale di un pentagono convesso regolare e stabilisce le proporzioni di un pentagono stellato regolare (pentagramma), le cui proprietà sono discusse in dettaglio nel libro.

Un pentagono a forma di stella è una figura simmetrica e, allo stesso tempo, la proporzione aurea asimmetrica appare nei rapporti dei suoi segmenti. Una tale combinazione di opposti attrae sempre con la sua profonda unità, la cui conoscenza consente di penetrare nelle leggi nascoste della natura e comprenderne l'eccezionale profondità e armonia. I Pitagorici, affascinati dalla consonanza dei segmenti del pentagono a forma di stella, lo scelsero come simbolo della loro comunità scientifica.

Sin dai tempi dell'astronomo I. Keplero (XVII secolo), a volte sono stati espressi diversi punti di vista riguardo a ciò che è più fondamentale: il teorema di Pitagora o la proporzione aurea. Il teorema di Pitagora è alla base della matematica, ne è uno dei capisaldi. rapporto aureoè alla base dell'armonia e della bellezza dell'universo. A prima vista, non è difficile da capire e non ha una completezza significativa. Tuttavia, alcune delle sue proprietà inaspettate e profonde sono state realizzate solo di recente, il che suggerisce la necessità di rispettarne la sottigliezza nascosta e la possibile versatilità. Il teorema di Pitagora e la proporzione aurea nel loro sviluppo sono strettamente intrecciati tra loro e con proprietà geometriche e algebriche. Non c’è alcun divario o differenza fondamentale tra loro. Non sono in competizione, hanno scopi diversi.

È del tutto possibile che entrambi i punti di vista siano uguali, poiché esiste un triangolo rettangolo contenente varie caratteristiche della proporzione aurea. In altre parole, esiste una figura geometrica che combina in modo abbastanza completo due sorprendenti fatti matematici: il teorema di Pitagora e la sezione aurea.

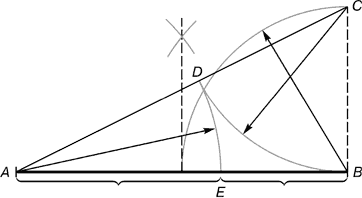
Per costruire un triangolo del genere è sufficiente estendere il lato Sole triangolo ABC(Fig. 4) fino all'intersezione nel punto E con la perpendicolare ripristinata nel punto UN di fianco AB(Fig. 5).

In un triangolo isoscele interno ASSO angolo φ (angolo ASSO) è pari a 144°, e l'angolo ψ (angoli EAC E AES) è pari a 18 o. Lato AC = SE = NE = D. Usando il teorema di Pitagora, è facile trovare la lunghezza della gamba

Usando questo risultato arriviamo facilmente alla relazione

Quindi è stata trovata una connessione diretta della radice sì 2 equazioni (4) - l'ultima delle radici delle equazioni (3) e (4) - con un angolo di 144 o. A questo proposito, il triangolo ASSO può essere chiamato il terzo triangolo della sezione aurea.

Se in un meraviglioso triangolo rettangolo AVE disegna la bisettrice dell'angolo TAXI finché non si interseca con il lato EV al punto F, poi lo vedremo a lato AB ci sono quattro angoli: 36 o, 72 o, 108 o e 144 o, con i quali le radici delle equazioni della proporzione aurea sono direttamente correlate (relazioni (7) - (10)). Pertanto, il triangolo rettangolo presentato contiene l'intera galassia di triangoli equilateri che hanno le caratteristiche della sezione aurea. Inoltre, è abbastanza notevole che sull'ipotenusa ci siano due segmenti qualsiasi Unione Europea= D E CF= 1.0 sono in relazione al rapporto aureo con FВ = D. L'angolo ψ è legato alle radici D E D equazioni (3) e (4) dalle relazioni

Le costruzioni dei triangoli isosceli presentate sopra, i cui angoli sono collegati alle radici delle equazioni della proporzione aurea, si basano sul segmento originale AB e le sue parti UN E B. Tuttavia, la sezione aurea consente di modellare non solo i triangoli sopra descritti, ma anche varie altre figure geometriche che portano elementi di relazioni armoniose.

Diamo due esempi di tali costruzioni. Nel primo, considera il segmento AB, presentato in Fig. 1. Veniamo al dunque CON- centro del cerchio, segmento B- raggio. Disegniamo un raggio B circonferenza e ad essa tangente da un punto UN(Fig. 6). Colleghiamo i punti di tangenza E E F con un punto CON. Il risultato è un rombo asimmetrico AECF, in cui la diagonale AC lo divide in due triangoli rettangoli uguali ASSO E ACF.

Prestiamo maggiore attenzione a uno di essi, ad esempio un triangolo ASSO. In questo triangolo l'angolo AES- retta, ipotenusa AC = UN, gamba SE = B e gamba AE = √ab≈ 0,486, che segue dalla relazione (2). Pertanto, gamba AEè la media geometrica (proporzionale) tra i segmenti UN E B, cioè esprime il centro geometrico di simmetria tra i numeri UN≈ 0,618 e B ≈ 0,382.

Troviamo gli angoli di questo triangolo:

Come nei casi precedenti, gli angoli δ e ε sono legati tramite il coseno alle radici delle equazioni (3) e (4).

Si noti che un rombo asimmetrico simile a un rombo AECF, si ottiene tracciando le tangenti dal punto IN ad una circonferenza di raggio UN e centrato nel punto UN.

Rombo asimmetrico AECF ottenuto in modo diverso nel libro analizzando i fenomeni di formazione e crescita nella natura vivente. Triangolo rettangolo AES chiamato in questo lavoro un triangolo “vivente”, poiché è in grado di generare immagini visive corrispondenti a vari elementi strutturali della natura e di servire come chiave nella costruzione di diagrammi geometrici dell'inizio dello sviluppo di alcuni organismi viventi.

Il secondo esempio è legato al primo e al terzo triangolo della sezione aurea. Dai primi due triangoli uguali della proporzione aurea formiamo un rombo con angoli interni di 72° e 108°. Allo stesso modo, combiniamo due terzi triangoli uguali della proporzione aurea in un rombo con angoli interni di 36° e 144°. Se i lati di questi rombi sono uguali tra loro, possono riempire un piano infinito senza vuoti o sovrapposizioni. L'algoritmo corrispondente per riempire l'aereo è stato sviluppato alla fine degli anni '70 del XX secolo dal fisico teorico dell'Università di Oxford R. Penrose. Inoltre, si è scoperto che nel mosaico risultante è impossibile selezionare una cella elementare con un numero intero di rombi di ciascun tipo, la cui traduzione permetterebbe di ottenere l'intero mosaico. Ma la cosa più notevole è che nell'infinito mosaico di Penrose il rapporto tra il numero di rombi “stretti” e il numero di rombi “larghi” è esattamente uguale al valore della sezione aurea D = 0,61803...!

In questo esempio, tutte le radici della sezione aurea, espresse attraverso gli angoli, sono sorprendentemente combinate con uno dei casi di riempimento non banale di un piano infinito con due figure elementari: i rombi.

In conclusione, notiamo che i vari esempi sopra riportati della connessione tra le radici delle equazioni della proporzione aurea e gli angoli dei triangoli illustrano il fatto che la proporzione aurea è un problema più ampio di quanto si pensasse in precedenza. Se in precedenza l'ambito di applicazione della proporzione aurea era in definitiva considerato il rapporto di segmenti e varie sequenze associate ai valori numerici delle sue radici (numeri di Fibonacci), ora si scopre che la proporzione aurea può generare una varietà di oggetti geometrici e le radici delle equazioni hanno un'espressione trigonometrica esplicita.

Gli autori sono consapevoli che il punto di vista sopra espresso riguardo all'eleganza dei rapporti matematici associati alla sezione aurea riflette esperienze estetiche personali. Nella letteratura filosofica moderna, i concetti di estetica e bellezza sono interpretati in modo abbastanza ampio e sono utilizzati piuttosto a livello intuitivo. Questi concetti si riferiscono principalmente all’art. Il contenuto della creatività scientifica in termini estetici non è praticamente considerato in letteratura. In prima approssimazione ai parametri estetici ricerca scientifica possiamo attribuire la loro relativa semplicità, la loro intrinseca simmetria e la capacità di generare immagini visive. Tutti questi parametri estetici sono soddisfatti da un compito chiamato “proporzione aurea”. In generale, i problemi dell’estetica nella scienza sono lungi dall’essere risolti, sebbene siano di grande interesse.

Si ha la sensazione intuitiva che la sezione aurea nasconda ancora i suoi segreti. Alcuni di loro, molto probabilmente, giacciono in superficie, in attesa dello sguardo insolito dei loro nuovi ricercatori. La conoscenza delle proprietà della sezione aurea può servire come una buona base per le persone creative, dando loro fiducia e scienza e dentro.

vita

LETTERATURA 1. Shevelev I. Sh., Marutaev I. A., Shmelev I. P. Sezione aurea: tre punti di vista sulla natura dell'armonia.

- M.: Stroyizdat, 1990. - 343 p. 2. Stakhov A. P. Codici del rapporto aureo.

- M.: Radio e comunicazione, 1984. - 152 p. 3. Vasyutinsky N. A. Rapporto aureo.

- M.: Giovane Guardia, 1990. - 238 p. 4. Korobko V.I. Proporzione aurea: alcuni aspetti filosofici dell'armonia.

- M. - Orel: 2000. - 204 p. 5. Urmantsev Yu. rapporto aureo

// Natura, 1968, n. 11. 6. Popkov V.V., Shipitsyn E.V. Sezione aurea nel ciclo di Carnot

// UFN, 2000, vol.170, n.11. 7. Konstantinov I. Fantasie con un dodecaedro

// Scienza e vita, 2001, n. 2. 8. Shevelev I. Sh. Armonia geometrica

// Scienza e vita, 1965, n. 8. 9. Gardner M. Dalle piastrellature di Penrose ai codici forti

Una persona distingue gli oggetti che lo circondano in base alla loro forma. L'interesse per la forma di un oggetto può essere dettato da necessità vitali, oppure può essere causato dalla bellezza della forma. La forma, che si basa su una combinazione di simmetria e rapporto aureo, favorisce la migliore percezione visiva e la comparsa di una sensazione di bellezza e armonia. Il tutto è sempre costituito da parti, parti di diverse dimensioni sono in un certo rapporto tra loro e con il tutto. Il principio della sezione aurea è la più alta manifestazione della perfezione strutturale e funzionale dell'insieme e delle sue parti nell'arte, nella scienza, nella tecnologia e nella natura.

Sezione aurea - proporzione armonica

In matematica proporzione(lat. proportio) chiama l'uguaglianza di due rapporti:

UN : B = C : D.

Segmento dritto AB può essere diviso in due parti nei seguenti modi:

in due parti uguali - AB : AC. = AB : AVANTI CRISTO.;
in due parti disuguali sotto ogni aspetto (tali parti non formano proporzioni);
quindi, quando AB : AC. = AC. : AVANTI CRISTO..

Quest'ultima è la divisione aurea ovvero la divisione di un segmento in rapporto estremo e medio.

La sezione aurea è tale divisione proporzionale di un segmento in parti disuguali, in cui l'intero segmento sta alla parte più grande come la parte più grande sta a quella più piccola; o in altre parole, il segmento più piccolo sta al più grande come il più grande sta al tutto:

UN : B = B : C
O
C : B = B : UN.

Riso. 1. Immagine geometrica della sezione aurea

La conoscenza pratica della sezione aurea inizia con la divisione di un segmento di linea retta nella proporzione aurea utilizzando un compasso e un righello.

Riso. 2.AVANTI CRISTO. = 1/2 AB; CD = AVANTI CRISTO.

Dal punto B si ripristina una perpendicolare pari alla metà AB. Punto ricevuto C collegato da una linea ad un punto UN. Sulla linea risultante viene tracciato un segmento AVANTI CRISTO. terminando con un punto D. Segmento ANNO DOMINI trasferito al diretto AB. Il punto risultante E divide un segmento AB nel rapporto del rapporto aureo.

I segmenti della sezione aurea sono espressi come una frazione irrazionale infinita A.E.= 0,618..., se AB prendi come uno ESSERE= 0,382... Per scopi pratici, vengono spesso utilizzati valori approssimativi di 0,62 e 0,38. Se il segmento AB preso come 100 parti, allora la parte più grande del segmento è uguale a 62 e la parte più piccola è 38 parti.

Le proprietà della sezione aurea sono descritte dall'equazione:

X 2 – X – 1 = 0.

Soluzione a questa equazione:

Le proprietà della sezione aurea hanno creato un’aura romantica di mistero e di culto quasi mistico attorno a questo numero.

Seconda sezione aurea

La rivista bulgara “Fatherland” (n. 10, 1983) ha pubblicato un articolo di Tsvetan Tsekov-Karandash “Sulla seconda sezione aurea”, che segue dalla sezione principale e fornisce un altro rapporto di 44: 56.

Questa proporzione si trova in architettura e si verifica anche quando si costruiscono composizioni di immagini di formato orizzontale allungato.

Riso. 3.

La divisione viene effettuata come segue. Segmento AB diviso secondo la sezione aurea. Dal punto C la perpendicolare viene ripristinata CD. Raggio AB c'è un punto D, che è collegato da una linea a un punto UN. Angolo retto ACDè diviso a metà. Dal punto C viene tracciata una linea finché non si interseca con la linea ANNO DOMINI. Punto E divide un segmento ANNO DOMINI rispetto a 56:44.

Riso. 4.

La figura mostra la posizione della linea della seconda sezione aurea. Si trova a metà strada tra la linea del rapporto aureo e la linea mediana del rettangolo.

Triangolo d'oro

Per trovare segmenti della proporzione aurea delle serie ascendente e discendente, puoi utilizzare pentagramma.

Riso. 5. Costruzione di un pentagono regolare e di un pentagramma

Per costruire un pentagramma, devi costruire un pentagono regolare. Il metodo di costruzione fu sviluppato dal pittore e grafico tedesco Albrecht Dürer (1471...1528). Permettere O– centro del cerchio, UN– un punto su una circonferenza e E– la metà del segmento O.A.. Perpendicolare al raggio O.A., restaurato al punto O, interseca il cerchio nel punto D. Usando un compasso, traccia un segmento sul diametro CE = ED. La lunghezza del lato di un pentagono regolare inscritto in una circonferenza è: DC. Disporre i segmenti sul cerchio DC e otteniamo cinque punti per disegnare un pentagono regolare. Colleghiamo gli angoli del pentagono tra loro con le diagonali e otteniamo un pentagramma. Tutte le diagonali del pentagono si dividono in segmenti collegati dalla sezione aurea.

Ciascuna estremità della stella pentagonale rappresenta un triangolo d'oro. I suoi lati formano all'apice un angolo di 36°, e la base, appoggiata di lato, lo divide nella proporzione della sezione aurea.

Riso. 6. Costruzione del triangolo d'oro

Effettuiamo una diretta AB. Dal punto UN adagiarvi sopra un segmento tre volte O valore arbitrario, attraverso il punto risultante P traccia una perpendicolare alla linea AB, sulla perpendicolare a destra e a sinistra del punto P mettere da parte i segmenti O. Punti ricevuti D E D 1 collegarsi con linee rette a un punto UN. Segmento gg metti 1 in linea Anno Domini 1, ottenendo un punto C. Ha diviso la linea Anno Domini 1 in proporzione alla sezione aurea. Linee Anno Domini 1 e gg 1 viene utilizzato per costruire un rettangolo “aureo”.

Storia della sezione aurea

È generalmente accettato che il concetto di divisione aurea sia stato introdotto nell'uso scientifico da Pitagora, un antico filosofo e matematico greco (VI secolo a.C.). Si presume che Pitagora abbia preso in prestito la sua conoscenza della divisione aurea dagli egiziani e dai babilonesi. In effetti, le proporzioni della piramide di Cheope, dei templi, dei bassorilievi, degli oggetti domestici e delle decorazioni della tomba indicano che gli artigiani egiziani utilizzavano i rapporti della divisione aurea durante la loro creazione. L'architetto francese Le Corbusier ha scoperto che nel rilievo del tempio del faraone Seti I ad Abydos e nel rilievo raffigurante il faraone Ramses, le proporzioni delle figure corrispondono ai valori della divisione aurea. L'architetto Khesira, raffigurato su un rilievo di una tavola di legno proveniente da una tomba a lui intitolata, tiene tra le mani strumenti di misura in cui sono registrate le proporzioni della divisione aurea.

I greci erano abili geometri. Insegnavano perfino l'aritmetica ai loro figli utilizzando le figure geometriche. Il quadrato pitagorico e la diagonale di questo quadrato furono la base per la costruzione di rettangoli dinamici.

Riso. 7. Rettangoli dinamici

Anche Platone (427...347 aC) conosceva la divisione aurea. Il suo dialogo “Timeo” è dedicato alle visioni matematiche ed estetiche della scuola pitagorica e, in particolare, alle questioni della divisione aurea.

La facciata dell'antico tempio greco del Partenone presenta proporzioni dorate. Durante i suoi scavi furono rinvenuti dei compassi utilizzati da architetti e scultori del mondo antico. Anche il compasso pompeiano (museo di Napoli) contiene le proporzioni della divisione aurea.

Riso. 8.

Nella letteratura antica giunta fino a noi, la divisione aurea fu menzionata per la prima volta negli Elementi di Euclide. Nel 2° libro degli Elementi viene data una costruzione geometrica della divisione aurea. Dopo Euclide, lo studio della divisione aurea fu portato avanti da Ipsicle (II secolo aC), Pappo (III secolo dC) ed altri. Europa medievale abbiamo conosciuto la divisione aurea Traduzioni arabe Gli "Inizi" di Euclide. Il traduttore J. Campano di Navarra (III secolo) ha commentato la traduzione. I segreti della Divisione d'Oro erano gelosamente custoditi e mantenuti in assoluta segretezza. Erano conosciuti solo dagli iniziati.

Durante il Rinascimento, l'interesse per la divisione aurea aumentò tra scienziati e artisti a causa del suo utilizzo sia nella geometria che nell'arte, soprattutto nell'architettura. Leonardo da Vinci, artista e scienziato, vide che gli artisti italiani avevano molta esperienza empirica, ma poca conoscenza . Concepì e iniziò a scrivere un libro sulla geometria, ma a quel tempo apparve un libro del monaco Luca Pacioli e Leonardo abbandonò la sua idea. Secondo i contemporanei e gli storici della scienza, Luca Pacioli fu un vero e proprio luminare, il più grande matematico italiano nel periodo compreso tra Fibonacci e Galileo. Luca Pacioli fu allievo del pittore Piero della Francesca, che scrisse due libri, uno dei quali si intitolava "Sulla prospettiva nella pittura". È considerato il creatore della geometria descrittiva.

Luca Pacioli capì perfettamente l'importanza della scienza per l'arte. Nel 1496, su invito del duca Moreau, venne a Milano, dove tenne lezioni di matematica. Leonardo da Vinci lavorò in quel periodo anche a Milano alla corte del Moro. Nel 1509, il libro di Luca Pacioli "La Divina Proporzione" fu pubblicato a Venezia con illustrazioni brillantemente eseguite, motivo per cui si ritiene che siano state realizzate da Leonardo da Vinci. Il libro era un inno entusiasta alla sezione aurea. Tra i tanti vantaggi della proporzione aurea, il monaco Luca Pacioli non mancò di nominare la sua “essenza divina” come espressione della Divina Trinità: Dio Padre, Dio Figlio e Dio Spirito Santo (era sottinteso che la piccola segmento è la personificazione di Dio Figlio, il segmento più grande è Dio Padre e l'intero segmento è Dio Spirito Santo).

E-book:

Mario Livio.

18/04/2011 A. F. Afanasyev Aggiornato il 16/06/12

Dimensioni e proporzioni sono uno dei compiti principali nella ricerca di un'immagine artistica di qualsiasi opera d'arte plastica. È chiaro che la questione delle dimensioni viene decisa tenendo conto della stanza in cui verrà collocato e degli oggetti che lo circondano.

Parlando di proporzioni (rapporti di valori dimensionali), li prendiamo in considerazione nel formato di un'immagine piatta (dipinto, intarsio), nei rapporti delle dimensioni complessive (lunghezza, altezza, larghezza) di un oggetto volumetrico, nel rapporto tra due oggetti di un insieme diversi in altezza o lunghezza, nel rapporto tra le dimensioni di due parti chiaramente visibili dello stesso oggetto, ecc.

Nei classici delle belle arti per molti secoli è stata tracciata una tecnica per costruire le proporzioni, chiamata sezione aurea, o numero aureo (questo termine è stato introdotto da Leonardo da Vinci). Il principio della sezione aurea, o simmetria dinamica, è che "il rapporto tra due parti di un tutto è uguale al rapporto tra la sua parte più grande e il tutto" (o, di conseguenza, tra il tutto e la parte più grande). Matematicamente è questo

il numero è espresso come - 1 ± 2?5 - che dà 1,6180339... o 0,6180339... Nell'arte, 1,62 è considerato il numero aureo, cioè un'espressione approssimativa del rapporto tra un valore maggiore in proporzione al suo valore minore valore .
Da approssimativo a più accurato, questo rapporto può essere espresso: ecc., dove: 5+3=8, 8+5=13, ecc. Oppure: 2,2:3,3:5,5:8 ,8, ecc. ., dove 2.2+3.3-5.5, ecc.

Graficamente, la sezione aurea può essere espressa dal rapporto tra i segmenti ottenuti da varie costruzioni. Più conveniente, a nostro avviso, è la costruzione mostrata in Fig. 169: se si aggiunge il suo lato corto alla diagonale di un mezzo quadrato, si ottiene un valore pari al rapporto tra il numero aureo e il suo lato lungo.

Riso. 169. Costruzione geometrica di un rettangolo nel rapporto aureo 1,62: 1. Numero aureo 1,62 in relazione ai segmenti (a e b)

Riso. 170. Costruzione grafica della funzione sezione aurea 1.12: 1

Proporzione di due rapporti aurei

crea una sensazione visiva di armonia ed equilibrio. Esiste un altro rapporto armonico tra due quantità adiacenti, espresso dal numero 1.12. È una funzione del numero aureo: se prendi la differenza tra due valori della sezione aurea, la dividi anche nella sezione aurea e aggiungi ogni frazione al valore più piccolo della sezione aurea originale, ottieni un rapporto di 1.12 (fig. 170). In questa relazione, ad esempio, l'elemento centrale (mensola) è disegnato con le lettere H, R, Z, ecc. In alcuni caratteri, per le lettere larghe vengono prese le proporzioni di altezza e larghezza, questa relazione si trova anche in natura.

Il numero aureo si osserva nelle proporzioni di una persona armoniosamente sviluppata (Fig. 171): la lunghezza della testa divide la distanza dalla vita alla corona in rapporto aureo; la rotula divide anche la distanza dalla vita alla pianta dei piedi; la punta del dito medio di una mano tesa divide l'intera altezza di una persona nella proporzione aurea; Anche il rapporto tra le falangi delle dita è un numero aureo. Lo stesso fenomeno si osserva in altre strutture della natura: nelle spirali dei molluschi, nelle corolle dei fiori, ecc.

Riso. 172. Proporzioni auree di foglia di geranio (pelargonium) intagliata. Costruzione: 1) Utilizzando un grafico in scala (vedi Fig. 171) costruiamo? ABC,	Riso. 173. Foglie di vite a cinque e tre petali. Il rapporto lunghezza/larghezza è 1,12. Viene espressa la sezione aurea

Nella fig. 172 e 173 mostrano la costruzione di un modello di una foglia di geranio (pelargonium) e di una foglia di vite nelle proporzioni dei numeri aurei 1,62 e 1,12. In una foglia di geranio la costruzione si basa su due triangoli: ABC e CEF, dove il rapporto tra altezza e base di ciascuno di essi è espresso dai numeri 0,62 e 1,62, e le distanze tra le tre coppie di punti più distanti dell'anta sono uguali: AB=CE=SF. La costruzione è indicata nel disegno. Il disegno di tale foglia è tipico dei gerani, che hanno foglie simili intagliate.

La foglia di sicomoro generalizzata (Fig. 173) ha le stesse proporzioni della foglia di vite, nel rapporto di 1,12, ma la proporzione maggiore della foglia di vite è la sua lunghezza, e quella della foglia di platano è la sua larghezza. La foglia del sicomoro ha tre dimensioni proporzionali in un rapporto di 1,62. Tale corrispondenza in architettura è chiamata triade (per quattro proporzioni - tetrade e oltre: pectad, esodo).

Nella fig. 174 mostra un metodo per costruire una foglia d'acero nelle proporzioni della sezione aurea. Con un rapporto larghezza/lunghezza di 1,12, ha diverse proporzioni con il numero 1,62. La costruzione si basa su due trapezi, in cui il rapporto tra altezza e lunghezza della base è espresso da un numero aureo. La costruzione è mostrata nel disegno e vengono fornite anche le opzioni per la forma di una foglia d'acero.

Nelle opere d'arte, un artista o uno scultore, consciamente o inconsciamente, fidandosi del suo occhio allenato, spesso applica il rapporto tra le dimensioni nella sezione aurea. Così, mentre lavorava su una copia della testa di Cristo (secondo Michelangelo), l'autore di questo libro notò che i riccioli adiacenti in ciocche di capelli nella loro dimensione riflettono il rapporto del rapporto aureo, e nella loro forma - la spirale di Archimede , l'evolvente. Il lettore può verificare personalmente che in numerosi dipinti di artisti classici la figura centrale si trova dai lati del formato a distanze che formano la proporzione della sezione aurea (ad esempio, la posizione della testa sia verticalmente che orizzontalmente in V . Ritratto di M. I. Lopukhina di Borovikovsky; posizione lungo il centro verticale della testa nel ritratto di A. S. Pushkin di O. Kiprensky e altri). La stessa cosa a volte può essere vista con il posizionamento della linea dell'orizzonte (F. Vasiliev: “Wet Meadow”, I. Levitan: “March”, “Evening Bells”).

Naturalmente questa regola non è sempre risolutiva del problema compositivo, e non deve sostituirsi all’intuizione del ritmo e delle proporzioni nel lavoro dell’artista. È noto, ad esempio, che alcuni artisti utilizzavano per le loro composizioni i rapporti dei “numeri musicali”: terze, quarte, quinte (2:3, 3:4, ecc.). Gli storici dell'arte, non senza ragione, notano che il design di qualsiasi monumento o scultura architettonica classica, se lo si desidera, può essere adattato a qualsiasi rapporto numerico. Il nostro compito in questo caso, e soprattutto il compito di un artista o intagliatore alle prime armi, è imparare a costruire una composizione deliberata della sua opera non secondo relazioni casuali, ma secondo proporzioni armoniose, comprovate dalla pratica. Queste proporzioni armoniose devono essere identificate ed enfatizzate dal design e dalla forma del prodotto.

Come esempio per trovare una proporzione armoniosa, si consideri la determinazione della dimensione della cornice per l'opera mostrata in Fig. 175. Il formato dell'immagine in essa collocata è fissato nella proporzione della sezione aurea. Dimensioni esterne le cornici con la stessa larghezza dei lati non daranno la proporzione aurea. Pertanto, il rapporto tra la sua lunghezza e larghezza (ЗЗ0X220) è considerato leggermente inferiore al numero d'oro, cioè uguale a 1,5, e la larghezza dei collegamenti trasversali è corrispondentemente aumentata rispetto ai lati laterali. Ciò ha permesso di arrivare alle dimensioni della cornice alla luce (per il dipinto), dando le proporzioni della sezione aurea. Il rapporto tra la larghezza del collegamento inferiore del telaio e la larghezza del collegamento superiore è regolato su un altro numero aureo, ovvero 1.12. Inoltre, il rapporto tra la larghezza del collegamento inferiore e la larghezza del collegamento laterale (94:63) è vicino a 1,5 (nella figura - l'opzione a sinistra).

Ora faremo un esperimento: aumenteremo il lato lungo del telaio a 366 mm a causa della larghezza del collegamento inferiore (sarà 130 mm) (nella foto - l'opzione a destra), che sarà avvicinare non solo il rapporto ma anche all'oro
numero 1.62 invece di 1.12. Il risultato è una nuova composizione che può essere utilizzata in qualche altro prodotto, ma per la cornice si desidera accorciarla. Copriamo la sua parte inferiore con un righello in modo che l'occhio “accetti” la proporzione risultante e otterremo la sua lunghezza di 330 mm, ad es. ci avvicineremo alla versione originale.

Quindi, analizzando varie opzioni(potrebbero essercene altre oltre alle due discusse), il maestro si ferma all'unica soluzione possibile dal suo punto di vista.

È meglio applicare il principio del rapporto aureo alla ricerca della composizione desiderata utilizzando un dispositivo semplice, il cui schema di progettazione di base è mostrato in Fig. 176. Due righelli di questo dispositivo possono, ruotando attorno al cardine B, formare un angolo arbitrario. Se, per qualsiasi soluzione angolare, dividiamo la distanza AC nella sezione aurea per un punto K e montiamo altri due righelli: KM\\BC e KE\\AB con cerniere nei punti K, E e M, allora per qualsiasi soluzione AC questa distanza verrà divisa per il punto K rispetto alla sezione aurea.

Vittorio Lavrus

Sezione aurea - proporzione armonica

In matematica proporzione(lat. proportio) chiama l'uguaglianza di due rapporti: UN : B = C : D.

Segmento dritto AB può essere diviso in due parti nei seguenti modi:

in due parti uguali - AB : AC = AB : Sole;

in due parti disuguali sotto ogni aspetto (tali parti non formano proporzioni);

quindi, quando AB : AC = AC : Sole.

Quest'ultima è la divisione aurea ovvero la divisione di un segmento in rapporto estremo e medio.

UN : B = B : C O Con : B = B : UN.

Riso. 1. Immagine geometrica della sezione aurea

La conoscenza pratica della sezione aurea inizia con la divisione di un segmento di linea retta nella proporzione aurea utilizzando un compasso e un righello.

Riso. 2. Dividere un segmento di linea retta utilizzando la sezione aurea. AVANTI CRISTO. = 1/2 AB; CD = AVANTI CRISTO.

Dal punto IN si ripristina una perpendicolare pari alla metà AB. Punto ricevuto CON collegato da una linea ad un punto UN. Sulla linea risultante viene tracciato un segmento Sole terminando con un punto D. Segmento ANNO DOMINI trasferito al diretto AB. Il punto risultante E divide un segmento AB nel rapporto del rapporto aureo.

Le proprietà della sezione aurea sono descritte dall'equazione:

X 2 - X - 1 = 0.

Soluzione a questa equazione:

Le proprietà della sezione aurea hanno creato un’aura romantica di mistero e di culto quasi mistico attorno a questo numero.

Seconda sezione aurea

La rivista bulgara "Fatherland" (n. 10, 1983) ha pubblicato un articolo di Tsvetan Tsekov-Karandash "Sulla seconda sezione aurea", che segue dalla sezione principale e fornisce un altro rapporto di 44: 56.

Questa proporzione si trova in architettura e si verifica anche quando si costruiscono composizioni di immagini di formato orizzontale allungato.

Riso. 3. Costruzione della seconda sezione aurea

La divisione viene eseguita come segue (vedi Fig. 3). Segmento AB diviso secondo la sezione aurea. Dal punto CON la perpendicolare viene ripristinata CD. Raggio AB c'è un punto D, che è collegato da una linea a un punto UN. Angolo retto ACDè diviso a metà. Dal punto CON viene tracciata una linea finché non si interseca con la linea ANNO DOMINI. Punto E divide un segmento ANNO DOMINI rispetto a 56:44.

Riso. 4. Dividere un rettangolo con la linea della seconda sezione aurea

Nella fig. La Figura 4 mostra la posizione della linea della seconda sezione aurea. Si trova a metà strada tra la linea del rapporto aureo e la linea mediana del rettangolo.

Triangolo d'oro

Per trovare segmenti della proporzione aurea delle serie ascendente e discendente, puoi utilizzare pentagramma.

Riso. 5. Costruzione di un pentagono regolare e di un pentagramma

Per costruire un pentagramma, devi costruire un pentagono regolare. Il metodo di costruzione fu sviluppato dal pittore e grafico tedesco Albrecht Dürer (1471...1528). Permettere O- centro del cerchio, UN- un punto su un cerchio e E- la metà del segmento OA. Perpendicolare al raggio OA, restaurato al punto DI, interseca il cerchio nel punto D. Usando un compasso, traccia un segmento sul diametro CE = ED. La lunghezza del lato di un pentagono regolare inscritto in una circonferenza è: DC. Disporre i segmenti sul cerchio DC e otteniamo cinque punti per disegnare un pentagono regolare. Colleghiamo gli angoli del pentagono tra loro con le diagonali e otteniamo un pentagramma. Tutte le diagonali del pentagono si dividono in segmenti collegati dalla sezione aurea.

Riso. 6. Costruzione del triangolo d'oro

Effettuiamo una diretta AB. Dal punto UN adagiarvi sopra un segmento tre volte DI valore arbitrario, attraverso il punto risultante R traccia una perpendicolare alla linea AB, sulla perpendicolare a destra e a sinistra del punto R mettere da parte i segmenti DI. Punti ricevuti D E D 1 collegarsi con linee rette a un punto UN. Segmento gg metti 1 in linea Anno Domini 1, ottenendo un punto CON. Ha diviso la linea Anno Domini 1 in proporzione alla sezione aurea. Linee Anno Domini 1 e gg 1 viene utilizzato per costruire un rettangolo “aureo”.

Storia della sezione aurea

È generalmente accettato che il concetto di divisione aurea sia stato introdotto nell'uso scientifico da Pitagora, un antico filosofo e matematico greco (VI secolo a.C.). Si presume che Pitagora abbia preso in prestito la sua conoscenza della divisione aurea dagli egiziani e dai babilonesi. In effetti, le proporzioni della piramide di Cheope, dei templi, dei bassorilievi, degli oggetti domestici e dei gioielli della tomba di Tutankhamon indicano che gli artigiani egiziani hanno utilizzato i rapporti della divisione aurea durante la loro creazione. L'architetto francese Le Corbusier ha scoperto che nel rilievo del tempio del faraone Seti I ad Abydos e nel rilievo raffigurante il faraone Ramses, le proporzioni delle figure corrispondono ai valori della divisione aurea. L'architetto Khesira, raffigurato su un rilievo di una tavola di legno proveniente da una tomba a lui intitolata, tiene tra le mani strumenti di misura in cui sono registrate le proporzioni della divisione aurea.

Riso. 7. Rettangoli dinamici

Riso. 8. Bussola antica con sezione aurea

Nella letteratura antica giunta fino a noi, la divisione aurea viene menzionata per la prima volta negli Elementi di Euclide. Nel 2° libro dei “Principi” viene data la costruzione geometrica della divisione aurea. Dopo Euclide, lo studio della divisione aurea fu condotto da Ipsicle (II secolo a.C.), Pappo (III secolo d.C.), ed altri l’Europa medievale, con la divisione aurea che abbiamo conosciuto attraverso le traduzioni arabe degli Elementi di Euclide. Il traduttore J. Campano di Navarra (III secolo) ha commentato la traduzione. I segreti della Divisione d'Oro erano gelosamente custoditi e mantenuti in assoluta segretezza. Erano conosciuti solo dagli iniziati.

Durante il Rinascimento, l'interesse per la divisione aurea aumentò tra scienziati e artisti a causa del suo utilizzo sia nella geometria che nell'arte, soprattutto nell'architettura. Leonardo da Vinci, artista e scienziato, vide che gli artisti italiani avevano molta esperienza empirica, ma poca conoscenza . Concepì e iniziò a scrivere un libro sulla geometria, ma a quel tempo apparve un libro del monaco Luca Pacioli e Leonardo abbandonò la sua idea. Secondo i contemporanei e gli storici della scienza, Luca Pacioli fu un vero e proprio luminare, il più grande matematico italiano nel periodo compreso tra Fibonacci e Galileo. Luca Pacioli era uno studente dell'artista Piero della Franceschi, che scrisse due libri, uno dei quali si intitolava "Sulla prospettiva nella pittura". È considerato il creatore della geometria descrittiva.

Luca Pacioli capì perfettamente l'importanza della scienza per l'arte. Nel 1496, su invito del duca di Moreau, venne a Milano, dove tenne conferenze di matematica. Leonardo da Vinci lavorò in quel periodo anche a Milano alla corte del Moro. Nel 1509, il libro di Luca Pacioli "La Divina Proporzione" fu pubblicato a Venezia con illustrazioni brillantemente eseguite, motivo per cui si ritiene che siano state realizzate da Leonardo da Vinci. Il libro era un inno entusiasta alla sezione aurea. Tra i tanti vantaggi della proporzione aurea, il monaco Luca Pacioli non mancò di nominare la sua “essenza divina” come espressione della trinità divina - Dio figlio, Dio padre e Dio spirito santo (era sottinteso che il piccolo segmento è la personificazione di Dio il figlio, il segmento più grande - Dio il padre e l'intero segmento - Dio dello Spirito Santo).

Anche Leonardo da Vinci prestò molta attenzione allo studio della divisione aurea. Realizzò sezioni di un corpo stereometrico formato da pentagoni regolari, e ogni volta ottenne dei rettangoli con proporzioni nella divisione aurea. Ecco perché ha dato il nome a questa divisione rapporto aureo. Quindi rimane ancora il più popolare.

Nello stesso periodo, nel Nord Europa, in Germania, Albrecht Dürer lavorava sugli stessi problemi. Abbozza l'introduzione alla prima versione del trattato sulle proporzioni. Scrive Dürer. “È necessario che qualcuno che sa fare una cosa la insegni ad altri che ne hanno bisogno. Questo è quello che ho deciso di fare."

A giudicare da una delle lettere di Dürer, mentre era in Italia ha incontrato Luca Pacioli. Albrecht Dürer sviluppa in dettaglio la teoria delle proporzioni del corpo umano. Dürer assegnò alla sezione aurea un posto importante nel suo sistema di relazioni. L'altezza di una persona è divisa in proporzioni auree dalla linea della cintura, nonché da una linea tracciata attraverso la punta del medio delle mani abbassate, la parte inferiore del viso vicino alla bocca, ecc. Il compasso proporzionale di Dürer è ben noto.

Grande astronomo del XVI secolo. Giovanni Keplero definì la sezione aurea uno dei tesori della geometria. Fu il primo a richiamare l'attenzione sull'importanza della proporzione aurea per la botanica (crescita delle piante e loro struttura).

Keplero definì la proporzione aurea autocontinua: “È strutturata in modo tale”, scrisse, “che i due termini più bassi di questa proporzione infinita si sommano al terzo termine, e a due eventuali ultimi termini, se sommati insieme. , date il termine successivo, e la stessa proporzione rimane fino all'infinito."

La costruzione di una serie di segmenti della proporzione aurea può essere fatta sia nel senso di aumento (serie crescente) che in quello di diminuzione (serie discendente).

Se su una linea retta di lunghezza arbitraria, metti da parte il segmento M, inserisci il segmento accanto ad esso M. Sulla base di questi due segmenti, costruiamo una scala di segmenti della proporzione aurea delle serie ascendente e discendente

Riso. 9. Costruzione di una scala di segmenti di proporzione aurea

Nei secoli successivi, la regola della proporzione aurea si trasformò in un canone accademico, e quando, col tempo, iniziò la lotta contro la routine accademica nell’arte, nel calore della lotta “buttarono via il bambino con l’acqua sporca”. La sezione aurea fu nuovamente “scoperta” a metà del XIX secolo. Nel 1855, il ricercatore tedesco della sezione aurea, il professor Zeising, pubblicò la sua opera “Studi estetici”. Ciò che accadde a Zeising fu esattamente ciò che inevitabilmente dovrebbe accadere ad un ricercatore che consideri un fenomeno come tale, senza collegamento con altri fenomeni. Ha assolutizzato la proporzione della sezione aurea, dichiarandola universale per tutti i fenomeni della natura e dell'arte. Zeising aveva numerosi seguaci, ma c’erano anche degli oppositori che dichiaravano la sua dottrina delle proporzioni “estetica matematica”.

Riso. 10. Proporzioni auree in parti del corpo umano

Zeising ha fatto un lavoro straordinario. Ne misurava circa duemila corpi umani e giunse alla conclusione che la sezione aurea esprime la legge statistica media. La divisione del corpo per il punto dell'ombelico è l'indicatore più importante della sezione aurea. Proporzioni corpo maschile oscillano all'interno del rapporto medio di 13: 8 = 1,625 e sono un po' più vicini alla sezione aurea rispetto alle proporzioni del corpo femminile, rispetto al quale il valore medio della proporzione è espresso nel rapporto 8: 5 = 1,6. Nel neonato il rapporto è 1:1, a 13 anni è 1,6, a 21 anni è uguale a quello di un uomo. Le proporzioni della sezione aurea appaiono anche in relazione ad altre parti del corpo: la lunghezza della spalla, dell'avambraccio e della mano, della mano e delle dita, ecc.

Riso. undici. Proporzioni auree nella figura umana

Zeising testò la validità della sua teoria sulle statue greche. Ha sviluppato le proporzioni dell'Apollo Belvedere nel modo più dettagliato. Sono stati esaminati vasi greci e strutture architettoniche epoche diverse, piante, animali, uova di uccelli, toni musicali, metri poetici. Zeising ha dato una definizione alla sezione aurea e ha mostrato come si esprime in segmenti di retta e in numeri. Quando furono ottenuti i numeri che esprimevano le lunghezze dei segmenti, Zeising vide che essi costituivano una serie di Fibonacci, che poteva essere continuata indefinitamente in una direzione o nell'altra. Il suo libro successivo era intitolato “La divisione aurea come legge morfologica fondamentale nella natura e nell’arte”. Nel 1876 in Russia fu pubblicato un piccolo libro, quasi un opuscolo, che descriveva quest'opera di Zeising. L'autore si rifugiò sotto le iniziali Yu.F.V. Questa edizione non menziona una sola opera di pittura.

IN fine XIX- inizio del XX secolo Sono apparse molte teorie puramente formalistiche sull'uso della sezione aurea nelle opere d'arte e nell'architettura. Con lo sviluppo del design e dell'estetica tecnica, la legge della sezione aurea si estese alla progettazione di automobili, mobili, ecc.

Serie di Fibonacci

Il nome del monaco matematico italiano Leonardo da Pisa, meglio conosciuto come Fibonacci (figlio di Bonacci), è indirettamente collegato alla storia della sezione aurea. Ha viaggiato molto in Oriente, ha introdotto l'Europa ai numeri indiani (arabi). Nel 1202 fu pubblicata la sua opera matematica "Il libro dell'abaco" (tavola di conteggio), che raccoglieva tutti i problemi conosciuti a quel tempo. Uno dei problemi diceva: “Quante coppie di conigli nasceranno da una coppia in un anno”. Riflettendo su questo argomento, Fibonacci costruì la seguente serie di numeri:

Una serie di numeri 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ecc. nota come serie di Fibonacci. La particolarità della sequenza numerica è che ciascuno dei suoi membri, a partire dal terzo, pari alla somma due precedenti 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34, ecc., e il rapporto dei numeri adiacenti nella serie si avvicina al rapporto della divisione aurea. Quindi, 21: 34 = 0,617 e 34: 55 = 0,618. Questa relazione è indicata dal simbolo F. Solo questo rapporto - 0,618: 0,382 - dà una divisione continua di un segmento di retta nella proporzione aurea, aumentandola o diminuendola all'infinito, quando il segmento minore sta a quello maggiore come il maggiore sta all'insieme.

Fibonacci si occupò anche delle esigenze pratiche del commercio: qual è il numero più piccolo di pesi che si possono utilizzare per pesare un prodotto? Fibonacci dimostra che il sistema di pesi ottimale è: 1, 2, 4, 8, 16...

Sezione aurea generalizzata

La serie di Fibonacci sarebbe potuta rimanere solo un incidente matematico, se non fosse stato per il fatto che tutti i ricercatori della divisione aurea nel mondo vegetale e animale, per non parlare dell'arte, arrivavano invariabilmente a questa serie come espressione aritmetica della legge dell'oro divisione.

Gli scienziati hanno continuato a sviluppare attivamente la teoria dei numeri di Fibonacci e della sezione aurea. Yu Matiyasevich risolve il decimo problema di Hilbert utilizzando i numeri di Fibonacci. Stanno emergendo metodi eleganti per risolvere una serie di problemi cibernetici (teoria della ricerca, giochi, programmazione) utilizzando i numeri di Fibonacci e la sezione aurea. Negli USA sta nascendo anche la Mathematical Fibonacci Association, che dal 1963 pubblica una rivista speciale.

Uno dei risultati in questo campo è la scoperta dei numeri di Fibonacci generalizzati e delle sezioni auree generalizzate.

La serie di Fibonacci (1, 1, 2, 3, 5, 8) e la serie “binaria” di pesi da lui scoperta 1, 2, 4, 8, 16... a prima vista sono completamente diverse. Ma gli algoritmi per la loro costruzione sono molto simili tra loro: nel primo caso ogni numero è la somma del numero precedente con se stesso 2 = 1 + 1; 4 = 2 + 2..., nel secondo è la somma dei due numeri precedenti 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2.... È possibile trovare una matematica generale formula da cui si ottiene e “serie binaria e serie di Fibonacci? O forse questa formula ce ne darà di nuove insiemi di numeri, in possesso di alcune nuove proprietà uniche?

Infatti, impostiamo il parametro numerico S, che può assumere qualsiasi valore: 0, 1, 2, 3, 4, 5... Consideriamo una serie di numeri, S+ 1 di cui i primi termini sono unità, e ciascuno dei successivi è pari alla somma di due termini del precedente e separati dal precedente da S passi. Se N Indichiamo l'esimo termine di questa serie con φ S ( N), allora otteniamo la formula generale φ S ( N) = φ S ( N- 1) + φ S ( N - S - 1).

È ovvio che quando S= 0 da questa formula si ottiene una serie “binaria”, con S= 1 - Serie di Fibonacci, con S= 2, 3, 4. nuova serie di numeri, che vengono chiamate S-Numeri di Fibonacci.

Nel complesso dorato S-la proporzione è la radice positiva dell'equazione aurea S-sezioni x S+1 - x S - 1 = 0.

È facile dimostrarlo quando S= 0, il segmento viene diviso a metà e quando S= 1 - il familiare rapporto aureo classico.

Rapporti tra vicini S- I numeri di Fibonacci coincidono con assoluta precisione matematica nel limite con l'oro S-proporzioni! I matematici in questi casi dicono che l'oro S-le sezioni sono invarianti numeriche S-Numeri di Fibonacci.

Fatti che confermano l'esistenza dell'oro S-sezioni in natura, cita lo scienziato bielorusso E.M. Soroko nel libro “Armonia strutturale dei sistemi” (Minsk, “Scienza e tecnologia”, 1984). Risulta, ad esempio, che le leghe binarie ben studiate hanno proprietà funzionali speciali e pronunciate (termostabile, dura, resistente all'usura, resistente all'ossidazione, ecc.) solo se peso specifico i componenti originali sono collegati tra loro da uno dei dorati S-proporzioni. Ciò ha permesso all'autore di avanzare l'ipotesi che l'oro S Le sezioni sono invarianti numerici dei sistemi auto-organizzanti. Una volta confermata sperimentalmente, questa ipotesi potrebbe essere di fondamentale importanza per lo sviluppo della sinergetica, un nuovo campo della scienza che studia i processi nei sistemi auto-organizzati.

Utilizzando i codici d'oro S-le proporzioni possono essere espresse da qualsiasi numero reale come somma di potenze dell'oro S-proporzioni a coefficienti interi.

La differenza fondamentale tra questo metodo di codifica dei numeri è che le basi dei nuovi codici, che sono d'oro S-proporzioni, con S> 0 risultano numeri irrazionali. Pertanto, i nuovi sistemi numerici con basi irrazionali sembrano mettere la gerarchia storicamente stabilita delle relazioni tra numeri razionali e irrazionali “dalla testa ai piedi”. Il fatto è che i numeri naturali furono prima “scoperti”; allora i loro rapporti sono numeri razionali. E solo più tardi – dopo la scoperta dei segmenti incommensurabili da parte dei Pitagorici – nacquero i numeri irrazionali. Ad esempio, nei sistemi decimale, quinario, binario e in altri sistemi numerici posizionali classici, i numeri naturali venivano scelti come una sorta di principio fondamentale - 10, 5, 2 - di cui certe regole tutti gli altri numeri naturali, così come i numeri razionali e irrazionali, furono costruiti.

Una sorta di alternativa ai metodi di notazione esistenti è un nuovo sistema irrazionale, come principio fondamentale, il cui inizio è un numero irrazionale (che, ricordiamo, è la radice dell'equazione del rapporto aureo); altri numeri reali sono già espressi attraverso di esso.

In un tale sistema numerico, any numero naturale sempre rappresentabile come finito - e non infinito, come si pensava in precedenza! - la somma dei gradi di qualsiasi oro S-proporzioni. Questo è uno dei motivi per cui l’aritmetica “irrazionale”, dotata di sorprendente semplicità ed eleganza matematica, sembra aver assorbito migliori qualità binaria classica e aritmetica di Fibonacci.

Principi di formazione in natura

Tutto ciò che ha preso una forma si è formato, è cresciuto, ha cercato di prendere posto nello spazio e di preservarsi. Questo desiderio si realizza principalmente in due opzioni: crescere verso l'alto o diffondersi sulla superficie della terra e torcersi a spirale.

Il guscio è attorcigliato a spirale. Se lo apri, ottieni una lunghezza leggermente inferiore alla lunghezza del serpente. Una piccola conchiglia di dieci centimetri ha una spirale lunga 35 cm. Le spirali sono molto comuni in natura. L’idea della sezione aurea sarebbe incompleta senza parlare della spirale.

Riso. 12. Spirale di Archimede

La forma della conchiglia arricciata a spirale attirò l'attenzione di Archimede. Lo studiò e trovò un'equazione per la spirale. La spirale disegnata secondo questa equazione è chiamata con il suo nome. L'aumento del suo passo è sempre uniforme. Attualmente, la spirale di Archimede è ampiamente utilizzata nella tecnologia.

Goethe sottolineò anche la tendenza della natura alla spiralità. La disposizione elicoidale e a spirale delle foglie sui rami degli alberi è stata notata molto tempo fa. La spirale è stata vista nella disposizione dei semi di girasole, delle pigne, degli ananas, dei cactus, ecc. Il lavoro congiunto di botanici e matematici ha fatto luce su questi aspetti fenomeni sorprendenti natura. Si è scoperto che la serie di Fibonacci si manifesta nella disposizione delle foglie su un ramo (filotassi), dei semi di girasole e delle pigne, e quindi si manifesta la legge della sezione aurea. Il ragno tesse la sua tela seguendo uno schema a spirale. Un uragano gira come una spirale. Gregge spaventato renna si allontana a spirale. La molecola del DNA è attorcigliata in una doppia elica. Goethe chiamò la spirale la “curva della vita”.

Tra le erbe lungo la strada cresce una pianta insignificante: la cicoria. Diamo un'occhiata più da vicino. Dal gambo principale si è formato un germoglio. La prima foglia si trovava proprio lì.

Riso. 13. Cicoria

Il germoglio fa una forte espulsione nello spazio, si ferma, rilascia una foglia, ma questa volta è più corta della prima, fa ancora una espulsione nello spazio, ma con meno forza, rilascia una foglia di dimensioni ancora più piccole e viene espulso di nuovo . Se la prima emissione è considerata pari a 100 unità, la seconda è pari a 62 unità, la terza a 38, la quarta a 24, ecc. Anche la lunghezza dei petali dipende dalla proporzione aurea. Crescendo e conquistando lo spazio, la pianta manteneva determinate proporzioni. Gli impulsi della sua crescita sono gradualmente diminuiti in proporzione alla sezione aurea.

Riso. 14. Lucertola vivipara

A prima vista, la lucertola ha proporzioni che piacciono ai nostri occhi: la lunghezza della sua coda è correlata alla lunghezza del resto del corpo da 62 a 38.

Sia nel mondo vegetale che in quello animale irrompe persistentemente la tendenza formativa della natura: la simmetria riguardo alla direzione della crescita e del movimento. Qui la sezione aurea appare nelle proporzioni delle parti perpendicolari alla direzione di crescita.

La natura ha effettuato la divisione in parti simmetriche e proporzioni auree. Le parti rivelano una ripetizione della struttura dell'insieme.

Riso. 15. uovo di uccello

Il grande Goethe, poeta, naturalista e artista (disegnava e dipingeva ad acquarelli), sognava di creare una dottrina unificata sulla forma, formazione e trasformazione dei corpi organici. Fu lui a introdurre il termine morfologia nell'uso scientifico.

Pierre Curie all'inizio di questo secolo formulò una serie di idee profonde sulla simmetria. Sosteneva che non si può considerare la simmetria di nessun corpo senza tenere conto della simmetria dell'ambiente.

I modelli di simmetria “dorata” si manifestano nelle transizioni energetiche particelle elementari, nella struttura di alcuni composti chimici, nei sistemi planetari e cosmici, nelle strutture genetiche degli organismi viventi. Questi modelli, come indicato sopra, esistono nella struttura dei singoli organi umani e del corpo nel suo insieme, e si manifestano anche nei bioritmi e nel funzionamento del cervello e nella percezione visiva.

Sezione aurea e simmetria

La sezione aurea non può essere considerata da sola, separatamente, senza connessione con la simmetria. Il grande cristallografo russo G.V. Wulf (1863...1925) considerava la sezione aurea una delle manifestazioni della simmetria.

La divisione aurea non è una manifestazione di asimmetria, qualcosa di opposto alla simmetria. Secondo le idee moderne, la divisione aurea è una simmetria asimmetrica. La scienza della simmetria include concetti come statico E simmetria dinamica. La simmetria statica caratterizza la pace e l'equilibrio, mentre la simmetria dinamica caratterizza il movimento e la crescita. Così, in natura, la simmetria statica è rappresentata dalla struttura dei cristalli, mentre nell'arte caratterizza la pace, l'equilibrio e l'immobilità. La simmetria dinamica esprime l'attività, caratterizza il movimento, lo sviluppo, il ritmo, è testimonianza della vita. La simmetria statica è caratterizzata da segmenti uguali e valori uguali. La simmetria dinamica è caratterizzata dall'aumento o dalla diminuzione dei segmenti e si esprime nei valori della sezione aurea di una serie crescente o decrescente.

Proporzioni auree in letteratura. Poesia e sezione aurea

Molto nella struttura delle opere poetiche rende questa forma d'arte simile alla musica. Un ritmo chiaro, una naturale alternanza di sillabe accentate e non accentate, un metro ordinato delle poesie e la loro ricchezza emotiva rendono la poesia sorella opere musicali. Ogni verso ha la propria forma musicale, il proprio ritmo e la propria melodia. Ci si può aspettare che nella struttura delle poesie appaiano alcune caratteristiche delle opere musicali, modelli di armonia musicale e, di conseguenza, la proporzione aurea.

Cominciamo con la dimensione della poesia, cioè il numero di versi in essa contenuti. Sembrerebbe che questo parametro della poesia possa cambiare arbitrariamente. Tuttavia, si è scoperto che non era così. Ad esempio, l'analisi di N. Vasyutinsky delle poesie di A.S. Pushkin da questo punto di vista ha mostrato che le dimensioni delle poesie sono distribuite in modo molto disomogeneo; si è scoperto che Pushkin preferisce chiaramente le dimensioni di 5, 8, 13, 21 e 34 linee (numeri di Fibonacci).

Molti ricercatori hanno notato che le poesie sono simili ai brani musicali; hanno anche punti culminanti che dividono il poema in proporzione alla sezione aurea. Consideriamo, ad esempio, la poesia di A.S. Il "Calzolaio" di Pushkin:

Un calzolaio una volta cercò il dipinto
E ha fatto notare l'errore nelle scarpe;
L'artista prese subito il pennello e si corresse,
Allora, con le braccia sui fianchi, il calzolaio continuò:
"Penso che la faccia sia un po' storta...
Non sono troppo nudi questi seni?
Qui Apelle interruppe impaziente:
"Giudice, amico mio, non più in alto dello stivale!"

ho un amico tenere d'occhio:
Non so di che materia si occupi
Era un esperto, anche se severo a parole,
Ma il diavolo lo odia per giudicare il mondo:
Prova a giudicare gli stivali!

Analizziamo questa parabola. La poesia è composta da 13 versi. Ha due parti semantiche: la prima in 8 righe e la seconda (la morale della parabola) in 5 righe (13, 8, 5 sono numeri di Fibonacci).

Una delle ultime poesie di Pushkin, "Non apprezzo molto i diritti forti..." è composta da 21 versi e ha due parti semantiche: 13 e 8 versi.

Non apprezzo molto i diritti rumorosi,
Il che fa girare più di una testa.
Non mi lamento che gli dei abbiano rifiutato
È il mio dolce destino contestare le tasse
O impedire ai re di combattersi tra loro;
E non mi basta preoccuparmi se la stampa è libera
Idioti in inganno o censura sensibile
Nei piani delle riviste il jolly è in imbarazzo.
Tutto questo, vedi, sono parole, parole, parole.
Altri, migliori diritti mi sono cari:
Ho bisogno di una libertà diversa, migliore:
Dipendi dal re, dipendi dal popolo -
Ci interessa? Dio sia con loro.
Nessuno
Non riferire solo a te stesso
Servire e compiacere; per il potere, per la livrea
Non piegare la tua coscienza, i tuoi pensieri, il tuo collo;
Vagare qua e là a piacimento,
Meravigliandosi della divina bellezza della natura,
E prima delle creazioni d'arte e di ispirazione
Tremando di gioia nell'estasi della tenerezza,
Che felicità! Giusto...

È caratteristico che la prima parte di questo verso (13 versi), secondo il suo contenuto semantico, sia divisa in 8 e 5 versi, cioè l'intera poesia è strutturata secondo le leggi della proporzione aurea.

Di indubbio interesse è l'analisi del romanzo "Eugene Onegin" realizzata da N. Vasyutinsky. Questo romanzo è composto da 8 capitoli, ciascuno con una media di circa 50 versi. L'ottavo capitolo è il più perfetto, il più raffinato ed emotivamente ricco. Ha 51 versi. Insieme alla lettera di Eugenio a Tatiana (60 righe), corrisponde esattamente al numero 55 di Fibonacci!

N. Vasyutinsky afferma:

"Il culmine del capitolo è la dichiarazione d'amore di Eugene per Tatyana - la riga "Impallidire e svanire... questa è felicità!" Questa riga divide l'intero ottavo capitolo in due parti - nella prima ci sono 477 righe, e nella seconda - 295 righe. Il loro rapporto è 1.617 ! La migliore corrispondenza al valore della proporzione aurea Questo è un grande miracolo di armonia, perfezionato dal genio di Pushkin!

La famosa poesia di Lermontov "Borodino" è divisa in due parti: un'introduzione indirizzata al narratore e che occupa solo una strofa ("Dimmi, zio, non è senza motivo..."), e parte principale, che rappresenta un tutto indipendente che si divide in due parti uguali. Il primo descrive l'anticipazione della battaglia con crescente tensione, il secondo descrive la battaglia stessa con una graduale diminuzione della tensione verso la fine del poema. Il confine tra queste parti è il punto culminante dell'opera e cade esattamente nel punto di divisione da parte della sezione aurea.

La parte principale della poesia è composta da 13 versi di sette versi, ovvero 91 versi. Avendolo diviso per la sezione aurea (91:1,618 = 56,238), siamo convinti che il punto di divisione sia all'inizio del versetto 57, dove c'è una breve frase: "Bene, è stata una giornata!". È questa frase che rappresenta il “punto culminante dell'emozionata anticipazione”, completando la prima parte del poema (anticipazione della battaglia) e aprendone la seconda parte (descrizione della battaglia).

Pertanto, la sezione aurea gioca un ruolo molto significativo nella poesia, evidenziando il culmine della poesia.

Sezione aurea in architettura, scultura, pittura, fotografia

Una delle opere più belle dell'architettura greca antica è il Partenone (V secolo a.C.).

Le figure mostrano una serie di modelli associati alla sezione aurea. Le proporzioni dell'edificio possono essere espresse mediante varie potenze del numero Ф=0,618...

Sulla pianta del Partenone si possono vedere anche i “rettangoli aurei”:

Possiamo vedere la sezione aurea nell'edificio della cattedrale Notre Dame di Parigi(Notre Dame de Paris), e nella Piramide di Cheope:

Le proporzioni della piramide di Cheope, dei templi, dei bassorilievi, degli oggetti domestici e dei gioielli della tomba di Tutankhamon indicano che gli artigiani egiziani hanno utilizzato i rapporti della divisione aurea durante la loro creazione. L'architetto francese Le Corbusier ha scoperto che nel rilievo del tempio del faraone Seti I ad Abydos e nel rilievo raffigurante il faraone Ramses, le proporzioni delle figure corrispondono ai valori della divisione aurea. L'architetto Khesira, raffigurato su un rilievo di una tavola di legno proveniente da una tomba a lui intitolata, tiene tra le mani strumenti di misura in cui sono registrate le proporzioni della divisione aurea.

Per quanto riguarda le piramidi, non solo le piramidi egiziane furono costruite secondo le perfette proporzioni della sezione aurea; lo stesso fenomeno è stato riscontrato nelle piramidi messicane. La sezione trasversale della piramide mostra una forma simile ad una scala. Il primo livello ha 16 gradini, il secondo 42 gradini e il terzo - 68 gradini.
Questi numeri si basano sul rapporto di Fibonacci come segue:

16 x 1,618 = 26

26 x 1,618 = 42

L'architettura della Cattedrale di San Basilio presenta molte proporzioni auree:

La proporzione aurea è stata utilizzata da molti scultori antichi. È nota la proporzione aurea della statua dell'Apollo Belvedere: l'altezza dell'uomo raffigurato è divisa dalla linea ombelicale nella sezione aurea.

Già nel Rinascimento, gli artisti scoprirono che ogni immagine ha alcuni punti che attirano involontariamente la nostra attenzione, i cosiddetti centri visivi. In questo caso, non importa quale sia il formato dell'immagine: orizzontale o verticale. Ci sono solo quattro di questi punti; dividono la dimensione dell'immagine orizzontalmente e verticalmente nella sezione aurea, cioè si trovano ad una distanza di circa 3/8 e 5/8 dai corrispondenti bordi del piano.

Questa scoperta fu chiamata dagli artisti dell'epoca la “sezione aurea” del dipinto. Pertanto, per attirare l'attenzione sull'elemento principale della fotografia, è necessario combinare questo elemento con uno dei centri visivi.

Nella foto I.I. "Shish Grove" di Shishkin mostra motivi della sezione aurea. Un pino brillantemente illuminato dal sole (in primo piano) divide la lunghezza del dipinto approssimativamente in rapporto aureo. A destra del pino c'è una collinetta soleggiata. Divide il lato destro dell'immagine orizzontalmente nella sezione aurea. A sinistra del pino principale ci sono molti pini: se lo desideri, puoi continuare con successo a dividere l'immagine nelle proporzioni della sezione aurea.

La presenza nell’immagine di verticali e orizzontali luminose, dividendola rispetto alla sezione aurea, conferisce un carattere di equilibrio e calma, secondo l’intenzione dell’artista. Quando un artista crea un'immagine con un'azione in rapido sviluppo, un tale schema compositivo geometrico (con una predominanza di verticali e orizzontali) diventa inaccettabile.

La sensazione di dinamica ed eccitazione si manifesta forse in modo più forte in un altro semplice figura geometrica- spirali. La composizione a più figure, eseguita nel 1509-1510 da Raffaello, quando il famoso pittore creò i suoi affreschi in Vaticano, si distingue per il dinamismo e la drammaticità della trama. Raffaello non portò mai a termine il suo piano, tuttavia, il suo schizzo fu inciso dallo sconosciuto grafico italiano Marcantinio Raimondi, che, sulla base di questo schizzo, creò l'incisione “La strage degli Innocenti”.

Se, nel bozzetto preparatorio di Raffaello, tracciamo mentalmente delle linee che partono dal centro semantico della composizione - il punto in cui le dita del guerriero si chiudono attorno alla caviglia del bambino - lungo le figure del bambino, della donna che lo tiene stretto, del guerriero con la spada sollevata, e poi lungo le figure dello stesso gruppo sulle parti di destra del disegno (nella figura queste linee sono disegnate in rosso), e poi collega questi pezzi con una linea tratteggiata curva, quindi con grande precisione viene tracciata una spirale aurea ottenuto. Ciò può essere verificato misurando il rapporto tra le lunghezze dei segmenti tagliati da una spirale su linee rette passanti per l'inizio della curva.

Non è noto se Raffaello abbia effettivamente disegnato la spirale aurea durante la creazione della composizione “La strage degli innocenti” o l’abbia solo “sentita”. Possiamo però affermare con sicurezza che l'incisore Raimondi ha visto questa spirale. Ciò è evidenziato dai nuovi elementi della composizione da lui aggiunti, sottolineando l'inversione della spirale nei punti in cui è indicata solo da una linea tratteggiata. Questi elementi possono essere visti nell'incisione finale di Raimondi: l'arco del ponte che si estende dalla testa della donna è sul lato sinistro della composizione e il corpo disteso del bambino è al centro.

Passando agli esempi della “sezione aurea” nella pittura, non si può fare a meno di concentrarsi sull’opera di Leonardo da Vinci. Osserviamo da vicino il dipinto "La Gioconda". La composizione del ritratto è basata su “triangoli d'oro”.

Moderno business modello utilizza anche proporzioni ideali, perché “tutto ciò che è nuovo è ben dimenticato vecchio”:

Fonti di informazione:

Kovalev F.V. Sezione aurea nella pittura. K.: Scuola Vyshcha, 1989.

Keplero I. A proposito dei fiocchi di neve esagonali. - M., 1982.

Dürer A. Diari, lettere, trattati - L., M., 1957.

Tsekov-Pencil Ts Informazioni sulla seconda sezione aurea. - Sofia, 1983.

Stakhov A. Codici della proporzione aurea.

Tagliando un quadrato di lato a da un rettangolo costruito secondo il principio della sezione aurea, otteniamo un nuovo rettangolo più piccolo con la stessa proprietà

D'oro sezione (proporzione aurea, divisione in rapporto estremo e medio, divisione armonica, numero di Fidia) - divisione di un valore continuo in parti in un rapporto tale in cui la parte più grande sta a quella più piccola come il valore intero sta a quella più grande. Ad esempio, dividendo un segmento AC in due parti in modo tale che la maggior parte di esso AB si riferisce al più piccolo Sole proprio come l'intero segmento AC si riferisce a AB(cioè | AB| / |Sole| = |AC| / |AB|).

Questa proporzione è solitamente indicata Lettera grecaϕ (si trova anche la designazione τ). È uguale a:

La formula delle “armonie auree”, che dà coppie di numeri che soddisfano la proporzione di cui sopra:

Nel caso di un numero, il parametro M = 1.

Nella letteratura antica giunta fino a noi, la divisione di un segmento in rapporto estremo e medio (ἄκρος καὶ μέσος λόγος ) trovato per la prima volta negli Elementi di Euclide (300 aC circa), dove viene utilizzato per costruire un pentagono regolare.

C Sonoil termine "sezione aurea" (tedesco)Schnitt più dorato) fu introdotto dal matematico tedesco Martin Ohm nel 1835.

Proprietà matematiche

Sezione aurea in una stella a cinque punte

— irrazionale numero algebrico, soluzione positiva di una qualsiasi delle seguenti equazioni

rappresentato da una frazione continua

Per le cui frazioni adatte sono i rapporti dei successivi numeri di Fibonacci. Così, .

In una normale stella a cinque punte, ogni segmento è diviso da un segmento che lo interseca nel rapporto aureo (ovvero il rapporto tra il segmento blu e quello verde, così come tra il segmento rosso e quello blu, nonché tra quello verde e quello viola). , sono uguali).

Costruzione della sezione aurea

Ecco un'altra visione:

Costruzione geometrica

Sezione aurea di un segmento AB può essere costruito come segue: al punto B perpendicolare a AB, posizionarvi sopra un segmento AVANTI CRISTO., pari alla metà AB, sul segmento AC. mettere da parte un segmento ANNO DOMINI, uguale AC. − C.B. e, infine, sul segmento AB mettere da parte un segmento A.E., uguale ANNO DOMINI. Poi

Sezione aurea e armonia

È generalmente accettato che gli oggetti contenenti la “sezione aurea” siano percepiti dalle persone come i più armoniosi. Le proporzioni della piramide di Cheope, dei templi, dei bassorilievi, degli oggetti domestici e dei gioielli della tomba di Tutankhamon indicano presumibilmente che gli artigiani egiziani utilizzavano i rapporti della sezione aurea durante la loro creazione. L’architetto Le Corbusier “scoprì” che nel rilievo del tempio del faraone Seti I ad Abydos e nel rilievo raffigurante il faraone Ramses, le proporzioni delle figure corrispondono ai valori della sezione aurea. L'architetto Khesira, raffigurato sul rilievo di una tavola di legno della tomba a lui intitolata, tiene tra le mani strumenti di misura in cui sono registrate le proporzioni della sezione aurea. La facciata dell'antico tempio greco del Partenone presenta proporzioni dorate. Durante i suoi scavi furono rinvenuti dei compassi utilizzati da architetti e scultori del mondo antico. Il compasso pompeiano (museo di Napoli) contiene anche le proporzioni della divisione aurea, ecc. ecc.

La “sezione aurea” di cui all’art

Sezione aurea e centri visivi

A partire da Leonardo da Vinci, molti artisti hanno utilizzato consapevolmente le proporzioni della sezione aurea.

È noto che Sergei Eisenstein ha costruito artificialmente il film La corazzata Potemkin secondo le regole della "sezione aurea". Ha spezzato il nastro in cinque parti. Innanzitutto tre azioni si svolge sulla nave. Negli ultimi due - a Odessa, dove si sta svolgendo la rivolta. Questa transizione verso la città avviene esattamente nel punto della sezione aurea. E ogni parte ha la propria frattura, che avviene secondo la legge della sezione aurea. In una cornice, scena, episodio c'è un certo salto nello sviluppo del tema: trama, stato d'animo. Eisenstein credeva che, poiché tale transizione è vicina al punto della sezione aurea, è percepita come la più logica e naturale.

Un altro esempio dell'uso della regola della sezione aurea nella cinematografia è la posizione dei componenti principali dell'inquadratura in punti speciali - "centri visivi". Spesso vengono utilizzati quattro punti, posti a distanze di 3/8 e 5/8 dai corrispondenti bordi del piano.

Va notato che negli esempi sopra riportati è apparso il valore approssimativo della “sezione aurea”: è facile verificare che né 3/2 né 5/3 sono uguali al valore della sezione aurea.

Anche l'architetto russo Zholtovsky ha utilizzato la sezione aurea.

Critica alla sezione aurea

Ci sono opinioni secondo cui il significato della sezione aurea nell'arte, nell'architettura e nella natura è esagerato e si basa su calcoli errati.

Quando si discute delle proporzioni ottimali dei rettangoli (formati carta A0 e multipli, dimensioni di lastre fotografiche (6:9, 9:12) o fotogrammi di film (spesso 2:3), dimensioni di schermi cinematografici e televisivi - ad esempio 3:4 o 9:16) sono state testate diverse opzioni. È venuto fuori che la maggior parte delle persone non percepisce l'oro sezione ottimale e ne considera le proporzioni “troppo allungate”.

Numero di letture: 8113