Hvem skapte det gylne snitt. Gylne proporsjoner i litteraturen

Kandidat for tekniske vitenskaper V. BELYANIN, ledende forsker ved det russiske forskningssenteret "Kurchatov Institute", E. ROMANOVA, student ved MADI (GTU)

Vitenskap og liv // Illustrasjoner

Det gylne snitt blir ikke undervist på skolen. Og da en av forfatterne av artikkelen foreslått nedenfor (Candidate of Technical Sciences V. Belyanin) snakket om det gylne snitt til en søker som planla å gå inn i MADI, i ferd med å forberede seg til eksamen ved instituttet, oppsto problemet uventet stor interesse og mange spørsmål, som ble besvart «på stedet». Vi bestemte oss for å lete etter dem sammen, og da ble det oppdaget finesser i det gylne snitt som tidligere hadde unngått forskere. Felles kreativitet har ført til arbeid som nok en gang bekrefter unge menneskers kreative evner og gir håp om at vitenskapens språk ikke vil gå tapt.

Mønstrene i matematikk, som mønstrene til en kunstner eller mønstrene til en poet, må være vakre; Ideer, som farger eller ord, må kombineres harmonisk. Skjønnhet er det første kriteriet: det er ingen plass i verden for stygg matematikk.
J.H. Hardy

skjønnhet matematisk problem fungerer som et av de viktigste insentivene for dens endeløse utvikling og årsaken til genereringen av en rekke applikasjoner. Noen ganger går det titalls, hundrevis og noen ganger tusenvis av år, men folk finner igjen og igjen uventede vendinger i en velkjent løsning og tolkningen av den. Et av disse langvarige og fascinerende problemene viste seg å være problemet med det gylne snitt (GR), som gjenspeiler elementene av nåde og harmoni i verden rundt oss. Det er forresten verdt å minne om at selv om andelen i seg selv var kjent for Euclid, ble begrepet "gyldent snitt" introdusert av Leonardo da Vinci (se "Vitenskap og liv").

Geometrisk sett innebærer det gyldne snitt å dele et segment i to ulike deler slik at den største delen er den gjennomsnittlige proporsjonal mellom hele segmentet og den mindre delen (fig. 1).

Algebraisk uttrykkes dette som følger:

Å studere denne andelen selv før du løser den viser at mellom segmentene en Og b Det er minst to overraskende forhold. For eksempel fra proporsjon (1) kan man enkelt få uttrykket

som setter forholdet mellom segmentene en, b, deres forskjell og sum. Derfor kan vi si forskjellig om det gylne snitt: to segmenter er i et harmonisk forhold hvis forskjellen deres relaterer seg til det mindre segmentet som det større segmentet forholder seg til summen deres.

Den andre relasjonen oppnås hvis det opprinnelige segmentet tas lik en: en + b= 1, som veldig ofte brukes i matematikk. I dette tilfellet

en 2 - b 2 = en - b = ab.

Fra disse resultatene følger to overraskende sammenhenger mellom segmentene EN Og b:

en 2 - b 2 = en - b = ab,(2)

som vil bli brukt i fremtiden.

La oss nå gå videre til å løse proporsjoner (1). I praksis benyttes to muligheter.

1. La oss betegne relasjonen en/b gjennom. Da får vi ligningen

x 2 - x - 1 = 0, (3)

Vanligvis vurderes bare den positive roten x 1, som gir en enkel og visuell inndeling av et segment i en gitt proporsjon. Faktisk, hvis vi tar hele segmentet som ett, bruker vi verdien av denne roten x 1, får vi en ≈ 0,618,b≈ 0,382.

Det er den positive roten x 1 i ligning (3) kalles oftest gyldne snitt eller andel av det gylne snitt. Den tilsvarende geometriske inndelingen av et segment kalles gyldne snitt(punktum MED i fig. 1).

For enkelhets skyld for videre presentasjon, la oss angi x 1 = D. Det er fortsatt ingen allment akseptert betegnelse for det gylne snitt. Dette skyldes tilsynelatende det faktum at det noen ganger blir forstått som et annet tall, som vil bli diskutert nedenfor.

Den negative roten, lagt til side som vanlig x 2 fører til en mindre klar inndeling av segmentet i to ulikt deler. Poenget er at det gir et skillepunkt MED, som ligger utenfor segmentet (den såkalte eksterne divisjonen). Faktisk, hvis en + b= 1, og bruk deretter roten x 2, får vi en ≈ -1,618, b≈ 2.618. Derfor segmentet en må legges i negativ retning (fig. 2).

2. Det andre alternativet for å løse proporsjon (1) er ikke fundamentalt forskjellig fra det første. Vi antar ukjent forhold b/en og angi det med y. Da får vi ligningen

y 2 + y -1 = 0 , (4)

som har irrasjonelle røtter

Hvis en + b= 1, og bruk deretter roten y 1, får vi en = y 1 ≈ 0,618, b≈ 0,382. For roten y 2 får vi en ≈ -1,618, b≈ 2.618. Geometrisk inndeling av et segment i forhold til det gylne snitt ved hjelp av røtter y 1 og y 2 er helt identisk med den forrige versjonen og tilsvarer fig. 1 og 2.

Positiv rot y 1 gir direkte ønsket løsning på problemet, og kalles også gyldne snitt .

For enkelhets skyld angir vi verdien av roten y 1 = d.

I litteraturen er altså den gyldne proporsjonen matematisk uttrykt med tallet D 1.618 eller nummer d 0,618, mellom hvilke det er to fantastiske forhold:

Dd= 1 og D - d = 1. (5)

Det er bevist at det ikke finnes andre lignende tallpar som har disse egenskapene.

Ved å bruke begge notasjonene for den gyldne proporsjonen skriver vi løsningene til likningene (3) og (4) i symmetrisk form: = D, = -d, = d, = -D.

De uvanlige egenskapene til det gylne snitt er beskrevet i tilstrekkelig detalj i litteraturen. De er så fantastiske at de har fanget sinnet til mange fremragende tenkere og skapt en aura av mystikk rundt dem.

Den gylne andelen finnes i konfigurasjonen av planter og mineraler, strukturen til deler av universet og den musikalske skalaen. Det gjenspeiler de globale naturprinsippene, og gjennomsyrer alle nivåer av organisering av levende og livløse gjenstander. Det brukes i arkitektur, skulptur, maleri, vitenskap, datateknologi og i design av husholdningsartikler. Kreasjoner som bærer konfigurasjonen av det gylne snitt virker proporsjonale og konsistente, er alltid behagelige for øyet, og matematisk språk Den gyldne proporsjonen er ikke mindre grasiøs og elegant.

I tillegg til likheter (5) fra relasjon (2), kan vi skille tre interessante relasjoner som har en viss perfeksjon og ser ganske attraktive og estetisk tiltalende ut:

(6)

Storheten og dybden i naturen kan merkes ikke bare, for eksempel når du ser på stjerner eller fjelltopper, men også ved å kikke på noen fantastiske formler, som er verdsatt av matematikere for deres skjønnhet. Disse inkluderer de elegante forholdene til den gylne proporsjonen, den fantastiske Euler-formelen e iπ = -1 (hvor Jeg= √-1), formelen som definerer det berømte Napier-tallet (grunnlaget for naturlige logaritmer): e = lim(1 + 1/ n) n = 2,718 at n→ ∞, og mange andre.

Etter å ha løst proporsjon (1), virker ideen ganske enkel, men som ofte er tilfellet med mange mennesker, ved første øyekast enkle oppgaver, det er mange finesser skjult i den. En av disse bemerkelsesverdige finessene, som forskere så langt har oversett, er forbindelsen mellom røttene til ligningene (3) og (4) med vinklene til tre fantastiske trekanter.

For å se dette, vurder hvordan et endimensjonalt linjestykke, delt i andelen av det gylne snitt, lett kan transformeres til et todimensjonalt bilde i form av en trekant. For å gjøre dette, bruk først fig. 1, legg til side på segmentet AB lengden på segmentet en to ganger - fra punktet EN mot poenget I og omvendt fra poenget I til siden EN. Vi får to poeng MED 1 og MED 2 deler segmentet AB fra forskjellige ender i forhold til det gylne snitt (fig. 3). Teller like segmenter AC 1 og Sol 2 radier, og punktene EN Og I sentre av sirklene, tegn to buer til de krysser hverandre på topppunktet MED. Se sammenhengen EN Og MED, og I Og MED, vi får en likebenet trekant ABC med partene AB = en + b = 1, AC = = sol = en = d≈ 0,618. Størrelsen på vinklene ved toppunktene EN Og I la oss betegne α, ved toppunktet MED- β. La oss beregne disse vinklene.

Ved cosinus-teoremet

(AB) 2 = 2(AC) 2 (1 - cos β).

Erstatter de numeriske verdiene til segmentene AB Og AC inn i denne formelen får vi

På samme måte får vi

(8)

Fremveksten av den gylne proporsjonen i et todimensjonalt bilde gjorde det mulig å koble røttene til ligningene (3) og (4) med vinklene til en trekant ABC, som kan kalles den første trekanten i det gylne snitt.

La oss utføre en lignende konstruksjon ved å bruke fig. 2. Hvis på fortsettelsen av segmentet AB utsette fra punkt I til høyre et segment som er like stort som segmentet en, og roter rundt sentrene EN Og I opp begge segmentene som radier til de berører, får vi andre trekant gyldne snitt(Fig. 4) . I denne likebenede trekanten, siden AB = en + b= 1, side AC = Sol = D≈1,618, og derfor, ved å bruke formelen til cosinussetningen, får vi

(9)

Vinkel a ved toppunktet MED er lik 36 o og er relatert til den gylne proporsjon ved relasjon (8). Som i forrige tilfelle er vinklene til denne trekanten relatert til røttene til ligningene (3) og (4).

Den andre trekanten til den gylne proporsjonen fungerer som hovedbestanddelen i en vanlig konveks femkant og setter proporsjonene til en vanlig stjerne femkant (pentagram), hvis egenskaper er diskutert i detalj i boken.

En stjerne femkant er en symmetrisk figur, og samtidig manifesteres den asymmetriske gyldne andelen i forholdet til segmentene. En slik kombinasjon av motsetninger tiltrekker seg alltid med sin dype enhet, hvis kunnskap lar en trenge inn i naturens skjulte lover og forstå deres eksepsjonelle dybde og harmoni. Pytagoreerne, betatt av konsonansen til segmentene i den stjerneformede femkanten, valgte den som et symbol på deres vitenskapelige fellesskap.

Siden tiden til astronomen I. Kepler (XVII århundre) har det noen ganger blitt uttrykt forskjellige synspunkter angående det som er mer grunnleggende - Pythagoras teorem eller den gyldne proporsjon. Pythagoras teoremet ligger i grunnlaget for matematikken, det er en av hjørnesteinene. Gyldent snitt ligger til grunn for harmonien og skjønnheten i universet. Ved første øyekast er det ikke vanskelig å forstå og har ikke betydelig grundighet. Noen av dets uventede og dyptgripende egenskaper har imidlertid først nylig blitt realisert, noe som tyder på behovet for å respektere dens skjulte subtilitet og mulige allsidighet. Pythagoras teorem og den gylne proporsjonen i deres utvikling er tett sammenvevd med hverandre og med geometriske og algebraiske egenskaper. Det er ingen gap eller grunnleggende forskjell mellom dem. De konkurrerer ikke, de har forskjellige formål.

Det er ganske mulig at begge synspunktene er like, siden det er en rettvinklet trekant som inneholder forskjellige trekk ved den gyldne proporsjonen. Med andre ord er det en geometrisk figur som ganske fullstendig kombinerer to fantastiske matematiske fakta - Pythagoras teorem og det gylne snitt.

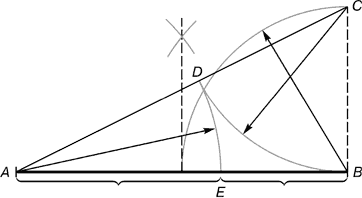
For å konstruere en slik trekant er det nok å forlenge siden Sol triangel ABC(Fig. 4) til krysset ved punktet E med perpendikulæren gjenopprettet på punktet EN til siden AB(Fig. 5).

I en indre likebenet trekant ESS vinkel φ (vinkel ESS) er lik 144°, og vinkelen ψ (vinkler ØK Og AES) er lik 18 o. Side AC = SE = NE = D. Ved å bruke Pythagoras teorem er det lett å finne ut at lengden på benet

Ved å bruke dette resultatet kommer vi lett frem til relasjonen

Så en direkte forbindelse av roten er funnet y 2 likninger (4) - den siste av røttene til likning (3) og (4) - med en vinkel på 144 o. I denne forbindelse trekanten ESS kan kalles den tredje trekanten i det gylne snitt.

Hvis i en fantastisk rettvinklet trekant AVE tegne vinkelhalveringslinjen DROSJE til den krysser siden EV på punktet F, så får vi se det langs siden AB det er fire vinkler: 36 o, 72 o, 108 o og 144 o, som røttene til de gyldne proporsjonsligningene er direkte relatert (relasjoner (7) - (10)). Dermed inneholder den presenterte rettvinklet hele galaksen av likesidede trekanter som har egenskapene til det gylne snitt. I tillegg er det ganske bemerkelsesverdig at på hypotenusen noen to segmenter EU= D Og CF= 1,0 er i forhold til det gylne snitt med FВ = d. Vinkelen ψ er relatert til røttene D Og d likning (3) og (4) ved relasjonene

Konstruksjonene av likebenede trekanter presentert ovenfor, hvis vinkler er koblet til røttene til ligningene til den gylne proporsjonen, er basert på det opprinnelige segmentet AB og dens deler en Og b. Imidlertid lar det gyldne forholdet deg modellere ikke bare trekantene beskrevet ovenfor, men også forskjellige andre geometriske figurer som bærer elementer av harmoniske forhold.

La oss gi to eksempler på slike konstruksjoner. I det første, vurder segmentet AB, presentert i fig. 1. La poenget MED- sentrum av sirkel, segment b- radius. La oss tegne en radius b sirkel og tangenter til den fra et punkt EN(Fig. 6). La oss koble sammen tangentpunktene E Og F med en prikk MED. Resultatet er en asymmetrisk rombe AECF, der diagonalen AC deler den inn i to like rette trekanter ESS Og ACF.

La oss være mer oppmerksom på en av dem, for eksempel en trekant ESS. I denne trekanten vinkelen AES- rett linje, hypotenuse AC = en, bein SE = b og bein AE = √ab≈ 0,486, som følger av relasjon (2). Derfor bein AE er det geometriske gjennomsnittet (proporsjonal) mellom segmentene en Og b, det vil si uttrykker det geometriske symmetrisenteret mellom tall en≈ 0,618 og b ≈ 0,382.

La oss finne vinklene til denne trekanten:

Som i tidligere tilfeller er vinklene δ og ε relatert gjennom cosinus til røttene til ligning (3) og (4).

Legg merke til at en asymmetrisk rombe ligner på en rombe AECF, fås ved å trekke tangenter fra punktet I til en sirkel med radius en og sentrert på punktet EN.

Asymmetrisk rombe AECF innhentet på en annen måte i boken når man analyserer dannelses- og vekstfenomenene i levende natur. Høyre trekant AES kalt en "levende" trekant i dette arbeidet, siden det er i stand til å generere visuelle bilder som tilsvarer ulike strukturelle elementer i naturen, og tjene som en nøkkel i å konstruere geometriske diagrammer av begynnelsen av utviklingen av noen levende organismer.

Det andre eksemplet er relatert til den første og tredje trekanten i det gylne snitt. Fra de to like første trekantene i den gylne proporsjonen danner vi en rombe med indre vinkler på 72° og 108°. På samme måte kombinerer vi to like tredje trekanter av den gylne proporsjonen til en rombe med indre vinkler på 36° og 144°. Hvis sidene til disse rombene er like med hverandre, kan de fylle et uendelig plan uten tomrom eller overlapping. Den tilsvarende algoritmen for å fylle flyet ble utviklet på slutten av 70-tallet av det tjuende århundre av en teoretisk fysiker fra Oxford University R. Penrose. Dessuten viste det seg at i den resulterende mosaikken er det umulig å velge en elementær celle med et helt antall romber av hver type, hvis oversettelse ville gjøre det mulig å skaffe hele mosaikken. Men det mest bemerkelsesverdige var at i den uendelige Penrose-mosaikken er forholdet mellom antall "smale" romber og antall "brede" nøyaktig lik verdien av det gylne snitt d = 0,61803...!

I dette eksemplet er alle røttene til det gylne snittet, uttrykt gjennom vinkler, overraskende kombinert med et av tilfellene av ikke-triviell fylling av et uendelig plan med to elementære figurer - romber.

Avslutningsvis legger vi merke til at de forskjellige eksemplene gitt ovenfor på sammenhengen mellom røttene til ligningene til den gyldne proporsjonen og vinklene til trekanter illustrerer det faktum at den gyldne proporsjonen er en mer omfattende oppgave enn tidligere forestilt. Hvis tidligere anvendelsesområdet for den gylne proporsjonen til slutt ble ansett for å være forholdet mellom segmenter og forskjellige sekvenser assosiert med de numeriske verdiene av røttene (Fibonacci-tall), nå er det oppdaget at den gylne proporsjonen kan generere en rekke geometriske objekter, og røttene til ligninger har et eksplisitt trigonometrisk uttrykk.

Forfatterne er klar over at synspunktet som er uttrykt ovenfor angående elegansen i de matematiske relasjonene knyttet til det gylne snitt reflekterer personlige estetiske erfaringer. I moderne filosofisk litteratur tolkes begrepene estetikk og skjønnhet ganske bredt og brukes heller på et intuitivt nivå. Disse konseptene relaterer seg hovedsakelig til kunst. Innholdet i vitenskapelig kreativitet i estetiske termer er praktisk talt ikke vurdert i litteraturen. Som en første tilnærming til estetiske parametere Vitenskapelig forskning vi kan tilskrive deres komparative enkelhet, deres iboende symmetri og evnen til å generere visuelle bilder. Alle disse estetiske parameterne oppfylles av en oppgave som kalles den "gyldne proporsjonen". Generelt er problemene med estetikk i vitenskapen langt fra løst, selv om de er av stor interesse.

Det føles intuitivt at det gylne snitt fortsatt skjuler sine hemmeligheter. Noen av dem ligger muligens på overflaten og venter på det uvanlige blikket til sine nye forskere. Kunnskap om egenskapene til det gylne snitt kan tjene som et godt grunnlag for kreative mennesker, gi dem selvtillit og vitenskap og i.

liv

LITTERATUR 1. Shevelev I. Sh., Marutaev I. A., Shmelev I. P. Gyldent snitt: Tre synspunkter på harmoniens natur.

- M.: Stroyizdat, 1990. - 343 s. 2. Stakhov A. P. Golden ratio-koder.

- M.: Radio og kommunikasjon, 1984. - 152 s. 3. Vasyutinsky N.A. Gyldent snitt.

- M.: Young Guard, 1990. - 238 s. 4. Korobko V. I. Gylden proporsjon: Noen filosofiske aspekter ved harmoni.

- M. - Orel: 2000. - 204 s. 5. Urmantsev Yu A. Gyldent snitt

// Nature, 1968, nr. 11. 6. Popkov V.V., Shipitsyn E.V. Gyldent snitt i Carnot-syklusen

// UFN, 2000, vol. 170, nr. 7. Konstantinov I. Fantasier med et dodekaeder

// Science and Life, 2001, nr. 2. 8. Shevelev I. Sh. Geometrisk harmoni

// Vitenskap og liv, 1965, nr. 8. 9. Gardner M. Fra Penrose-flislegging til sterke chiffer

En person skiller gjenstander rundt seg ved deres form. Interessen for formen til et objekt kan dikteres av vital nødvendighet, eller det kan være forårsaket av formens skjønnhet. Formen, hvis konstruksjon er basert på en kombinasjon av symmetri og det gylne snitt, bidrar til den beste visuelle oppfatningen og utseendet til en følelse av skjønnhet og harmoni. Helheten består alltid av deler, deler av ulik størrelse står i et visst forhold til hverandre og til helheten. Prinsippet om det gylne snitt er den høyeste manifestasjonen av den strukturelle og funksjonelle perfeksjonen av helheten og dens deler i kunst, vitenskap, teknologi og natur.

Gyldent forhold - harmonisk proporsjon

I matematikk proporsjon(lat. proportio) kaller likheten mellom to relasjoner:

en : b = c : d.

Rett segment AB kan deles inn i to deler på følgende måter:

i to like deler - AB : A.C. = AB : B.C.;
i to ulike deler på noen måte (slike deler danner ikke proporsjoner);
altså når AB : A.C. = A.C. : B.C..

Sistnevnte er den gylne divisjonen eller delingen av et segment i ekstreme og gjennomsnittlige forhold.

Det gylne snitt er en slik proporsjonal inndeling av et segment i ulik deler, der hele segmentet er relatert til den større delen som den større delen selv er relatert til den mindre; eller med andre ord, det mindre segmentet er til det større som det større er for helheten:

en : b = b : c
eller
c : b = b : en.

Ris. 1. Geometrisk bilde av det gylne snitt

Praktisk bekjentskap med det gyldne snitt begynner med å dele et rett linjesegment i den gyldne proporsjonen ved hjelp av et kompass og linjal.

Ris. 2.B.C. = 1/2 AB; CD = B.C.

Fra punkt B en perpendikulær lik halvparten gjenopprettes AB. Mottatt poeng C forbundet med en linje til et punkt EN. Et segment plottes på den resulterende linjen B.C. slutter med en prikk D. Linjestykke AD overført til direkte AB. Det resulterende punktet E deler et segment AB i det gylne snitt.

Segmenter av det gylne snitt uttrykkes som en uendelig irrasjonell brøkdel A.E.= 0,618..., hvis AB ta som en VÆRE= 0,382... For praktiske formål brukes ofte omtrentlige verdier på 0,62 og 0,38. Hvis segmentet AB tatt som 100 deler, så er den største delen av segmentet lik 62, og den mindre delen er 38 deler.

Egenskapene til det gylne snitt er beskrevet av ligningen:

x 2 – x – 1 = 0.

Løsning på denne ligningen:

Egenskapene til det gylne snitt har skapt en romantisk aura av mystikk og nesten mystisk tilbedelse rundt dette nummeret.

Andre gylne snitt

Det bulgarske magasinet “Fatherland” (nr. 10, 1983) publiserte en artikkel av Tsvetan Tsekov-Karandash “On the second golden section”, som følger av hoveddelen og gir et annet forhold på 44:56.

Denne andelen finnes i arkitektur, og oppstår også når man konstruerer komposisjoner av bilder av et langstrakt horisontalt format.

Ris. 3.

Inndelingen utføres som følger. Linjestykke AB delt etter det gylne snitt. Fra punkt C perpendikulæren gjenopprettes CD. Radius AB det er et poeng D, som er forbundet med en linje til et punkt EN. Rett vinkel ACD er delt i to. Fra punkt C en linje trekkes til den skjærer linjen AD. Punktum E deler et segment AD i forhold til 56:44.

Ris. 4.

Figuren viser posisjonen til linjen til det andre gylne snittet. Den er plassert midt mellom den gyldne snittlinjen og midtlinjen i rektangelet.

Gylden trekant

For å finne segmenter av den gylne andelen av stigende og synkende serier, kan du bruke pentagram.

Ris. 5. Konstruksjon av en vanlig femkant og pentagram

For å bygge et pentagram, må du bygge en vanlig femkant. Metoden for konstruksjonen ble utviklet av den tyske maleren og grafikeren Albrecht Durer (1471...1528). La O- sentrum av sirkelen, EN– et punkt på en sirkel og E– midten av segmentet O.A.. Vinkelrett på radius O.A., gjenopprettet på punktet O, skjærer sirkelen i punktet D. Bruk et kompass til å tegne et segment på diameteren C.E. = ED. Sidelengden til en vanlig femkant innskrevet i en sirkel er DC. Legg ut segmenter på sirkelen DC og vi får fem poeng for å trekke en vanlig femkant. Vi kobler hjørnene på femkanten gjennom hverandre med diagonaler og får et femkant. Alle diagonaler i femkanten deler hverandre i segmenter forbundet med det gylne snitt.

Hver ende av den femkantede stjernen representerer en gylden trekant. Sidene danner en vinkel på 36° på toppen, og basen, lagt på siden, deler den i forholdet til det gylne snitt.

Ris. 6. Konstruksjon av den gylne trekanten

Vi gjennomfører en direkte AB. Fra punkt EN legg et segment på den tre ganger O vilkårlig verdi, gjennom det resulterende punktet P tegne en vinkelrett på linjen AB, på vinkelrett til høyre og venstre for punktet P sett til side segmentene O. Fikk poeng d Og d 1 koble med rette linjer til et punkt EN. Linjestykke dd sett 1 på streken Annonse 1, får et poeng C. Hun delte linjen Annonse 1 i forhold til det gylne snitt. Linjer Annonse 1 og dd 1 brukes til å konstruere et "gyllent" rektangel.

Historien om det gylne snitt

Det er generelt akseptert at konseptet med den gylne inndelingen ble introdusert i vitenskapelig bruk av Pythagoras, en gammel gresk filosof og matematiker (VI århundre f.Kr.). Det er en antagelse om at Pythagoras lånte sin kunnskap om den gylne divisjonen fra egypterne og babylonerne. Faktisk indikerer proporsjonene til Cheops-pyramiden, templene, basrelieffer, husholdningsartikler og dekorasjoner fra graven at egyptiske håndverkere brukte forholdene til den gylne divisjonen når de laget dem. Den franske arkitekten Le Corbusier fant at i relieffet fra tempelet til farao Seti I i Abydos og i relieffet som viser farao Ramses, samsvarer proporsjonene av figurene med verdiene til den gylne inndelingen. Arkitekten Khesira, avbildet på et relieff av en treplate fra en grav oppkalt etter ham, holder i hendene måleinstrumenter der proporsjonene til den gylne inndelingen er registrert.

Grekerne var dyktige geometre. De lærte til og med aritmetikk til barna sine ved å bruke geometriske figurer. Det pytagoreiske kvadratet og diagonalen til dette kvadratet var grunnlaget for konstruksjonen av dynamiske rektangler.

Ris. 7. Dynamiske rektangler

Platon (427...347 f.Kr.) visste også om den gylne inndelingen. Dialogen hans "Timaeus" er dedikert til de matematiske og estetiske synspunktene til den pytagoreiske skolen og spesielt til spørsmålene om den gylne divisjonen.

Fasaden til det gamle greske tempelet i Parthenon har gylne proporsjoner. Under utgravningene ble det oppdaget kompass som ble brukt av arkitekter og skulptører fra den antikke verden. Det pompeianske kompasset (museet i Napoli) inneholder også proporsjonene til den gylne inndelingen.

Ris. 8.

I den antikke litteraturen som har kommet ned til oss, ble den gylne inndelingen først nevnt i Euklids elementer. I elementets 2. bok er det gitt en geometrisk konstruksjon av den gylne inndelingen. Etter Euclid ble studiet av gylden divisjon utført av Hypsicles (II århundre f.Kr.), Pappus (III århundre e.Kr.) og andre. middelalderens Europa vi ble kjent med den gylne divisjonen gjennom Arabiske oversettelser Euklids "Begynnelser". Oversetteren J. Campano fra Navarra (III århundre) kom med kommentarer til oversettelsen. Hemmelighetene til den gylne divisjonen ble nidkjært bevoktet og holdt i streng hemmelighet. De var bare kjent for innviede.

Under renessansen økte interessen for den gyldne divisjonen blant forskere og kunstnere på grunn av dens bruk i både geometri og kunst, spesielt innen arkitektur, Leonardo da Vinci, en kunstner og vitenskapsmann, så at italienske kunstnere hadde mye empirisk erfaring, men lite. kunnskap. Han ble unnfanget og begynte å skrive en bok om geometri, men på den tiden dukket det opp en bok av munken Luca Pacioli, og Leonardo forlot ideen. I følge samtidige og vitenskapshistorikere var Luca Pacioli en ekte lysmann, den største matematikeren i Italia i perioden mellom Fibonacci og Galileo. Luca Pacioli var elev av maleren Piero della Francesca, som skrev to bøker, hvorav den ene hadde tittelen "On Perspective in Painting". Han regnes som skaperen av beskrivende geometri.

Luca Pacioli forsto perfekt betydningen av vitenskap for kunst. I 1496, på invitasjon fra hertug Moreau, kom han til Milano, hvor han holdt forelesninger om matematikk. Leonardo da Vinci jobbet også i Milano ved Moro-domstolen på den tiden. I 1509 ble Luca Paciolis bok "The Divine Proportion" utgitt i Venezia med strålende utførte illustrasjoner, og det er derfor det antas at de ble laget av Leonardo da Vinci. Boken var en entusiastisk salme til det gylne snitt. Blant de mange fordelene med den gyldne proporsjon, unnlot ikke munken Luca Pacioli å navngi dens "guddommelige essens" som et uttrykk for den guddommelige treenighet - Gud Faderen, Gud Sønnen og Gud Den Hellige Ånd (det ble antydet at den lille segmentet er personifiseringen av Gud Sønnen, det større segmentet er Gud Faderen, og hele segmentet - Gud den Hellige Ånd).

E-bøker:

Mario Livio.

18.04.2011 A. F. Afanasyev Oppdatert 16.06.12

Dimensjoner og proporsjoner er en av hovedoppgavene i søket etter et kunstnerisk bilde av ethvert plastisk kunstverk. Det er klart at spørsmålet om størrelse avgjøres under hensyntagen til rommet der det skal ligge og gjenstandene rundt det.

Når vi snakker om proporsjoner (forhold mellom dimensjonale verdier), tar vi hensyn til dem i formatet til et flatt bilde (maleri, marquetry), i forholdet mellom de totale dimensjonene (lengde, høyde, bredde) til et volumetrisk objekt, i forholdet mellom to gjenstander av ett ensemble forskjellige i høyde eller lengde, i forholdet størrelsene til to klart synlige deler av samme gjenstand, etc.

I klassikerne innen kunst i mange århundrer har en teknikk for å konstruere proporsjoner blitt sporet, kalt det gylne snitt, eller det gylne tallet (dette begrepet ble introdusert av Leonardo da Vinci). Prinsippet for det gyldne snitt, eller dynamisk symmetri, er at "forholdet mellom to deler av en enkelt helhet er lik forholdet mellom dens største del og helheten" (eller følgelig helheten til den større delen). Matematisk er dette

tallet er uttrykt som - 1 ± 2?5 - som gir 1,6180339... eller 0,6180339... I kunst er 1,62 tatt som det gylne tall, dvs. et omtrentlig uttrykk for forholdet mellom en større verdi i forhold til dens mindre verdi .
Fra omtrentlig til mer nøyaktig kan dette forholdet uttrykkes: osv., hvor: 5+3=8, 8+5=13 osv. Eller: 2,2:3,3:5,5:8 ,8 osv. ., hvor 2,2+3,3-5,5 osv.

Grafisk kan det gyldne snitt uttrykkes ved forholdet mellom segmenter oppnådd ved forskjellige konstruksjoner. Mer praktisk, etter vår mening, er konstruksjonen vist i fig. 169: hvis du legger den korte siden til diagonalen til en halv firkant, får du en verdi i forholdet mellom det gylne tallet og langsiden.

Ris. 169. Geometrisk konstruksjon av et rektangel i det gylne snitt 1,62: 1. Gyldent tall 1,62 i forhold til segmentene (a og b)

Ris. 170. Grafisk konstruksjon av funksjonen gyldne snitt 1,12:1

Andel av to gylne snitt

skaper en visuell følelse av harmoni og balanse. Det er et annet harmonisk forhold mellom to tilstøtende mengder, uttrykt med tallet 1,12. Det er en funksjon av det gyldne tallet: hvis du tar forskjellen mellom to verdier av det gyldne snitt, deler det også i det gyldne snitt og legger hver brøk til den minste verdien av det opprinnelige gyldne snitt, får du et forhold på 1,12 (fig. 170). I denne relasjonen er for eksempel det midterste elementet (hyllen) tegnet i bokstavene H, R, Z osv. i noen fonter, proporsjoner av høyde og bredde er tatt for brede bokstaver, denne relasjonen finnes også i naturen.

Det gylne tallet observeres i proporsjonene til en harmonisk utviklet person (fig. 171): lengden på hodet deler avstanden fra midjen til toppen av hodet i det gylne snitt; kneskålen deler også avstanden fra midjen til fotsålen; spissen av langfingeren til en utstrakt hånd deler hele høyden til en person i den gylne proporsjonen; Forholdet mellom phalanges av fingrene er også et gyldent tall. Det samme fenomenet er observert i andre strukturer i naturen: i spiralene til bløtdyr, i kronene til blomster, etc.

Ris. 172. Gylne proporsjoner av et utskåret geraniumblad (pelargonium). Konstruksjon: 1) Ved hjelp av en skalagraf (se fig. 171) bygger vi? ABC,	Ris. 173. Fembladede og trebladede drueblader. Forholdet mellom lengde og bredde er 1,12. Det gylne snitt er uttrykt

I fig. 172 og 173 viser konstruksjonen av et mønster av et geranium (pelargonium) blad og et drueblad i proporsjonene av gylne tall 1,62 og 1,12. I et geraniumblad er konstruksjonen basert på to trekanter: ABC og CEF, hvor forholdet mellom høyden og bunnen av hver av dem er uttrykt med tallene 0,62 og 1,62, og avstandene mellom de tre parene av de fjerneste punktene av bladet er like: AB=CE=SF. Konstruksjonen er angitt på tegningen. Utformingen av et slikt blad er typisk for geranier, som har lignende utskårne blader.

Det generaliserte platanbladet (fig. 173) har samme proporsjoner som druebladet, i forholdet 1,12, men den største andelen av druebladet er lengden, og platanbladet er bredden. Platanbladene har tre proporsjonale størrelser i forholdet 1,62. En slik korrespondanse i arkitektur kalles en triade (for fire proporsjoner - tetrad og videre: pectad, heksode).

I fig. 174 viser en metode for å konstruere et lønneblad i proporsjonene til det gylne snitt. Med et forhold mellom bredde og lengde på 1,12 har den flere proporsjoner med tallet 1,62. Konstruksjonen er basert på to trapeser, der forholdet mellom høyde og lengde på basen er uttrykt med et gyldent tall. Konstruksjonen er vist på tegningen, og det er også gitt muligheter for formen til et lønneblad.

I kunstverk bruker en kunstner eller skulptør, bevisst eller ubevisst, som stoler på sitt trente øye, ofte forholdet mellom størrelser i det gylne snitt. Mens han jobbet med en kopi av Kristi hode (ifølge Michelangelo), la forfatteren av denne boken merke til at tilstøtende krøller i hårstrå i størrelsen gjenspeiler forholdet mellom det gylne snitt og i form - den arkimedeiske spiralen, det involvente. Leseren kan selv se at i en rekke malerier av klassiske kunstnere er den sentrale figuren plassert fra sidene av formatet i avstander som utgjør andelen av det gylne snitt (for eksempel plasseringen av hodet både vertikalt og horisontalt i V . Borovikovskys portrett av M. I. Lopukhina posisjon langs det vertikale midten av hodet i portrettet av A. S. Pushkin av O. Kiprensky og andre). Det samme kan noen ganger sees med plasseringen av horisontlinjen (F. Vasiliev: "Wet Meadow", I. Levitan: "March", "Evening Bells").

Selvfølgelig er denne regelen ikke alltid en løsning på problemet med komposisjon, og den bør ikke erstatte intuisjonen av rytme og proporsjoner i kunstnerens arbeid. Det er for eksempel kjent at noen artister brukte forholdet mellom "musikalske tall" for sine komposisjoner: tredjedeler, fjerdedeler, femtedeler (2:3, 3:4, etc.). Kunsthistorikere, ikke uten grunn, bemerker at utformingen av ethvert klassisk arkitektonisk monument eller skulptur, om ønskelig, kan justeres til et hvilket som helst tallforhold. Vår oppgave i dette tilfellet, og spesielt oppgaven til en begynnende kunstner eller treskjærer, er å lære å bygge en bevisst komposisjon av hans verk, ikke i henhold til tilfeldige forhold, men i henhold til harmoniske proporsjoner, bevist ved praksis. Disse harmoniske proporsjonene må identifiseres og fremheves av produktets design og form.

Som et eksempel på å finne en harmonisk proporsjon, vurder å bestemme størrelsen på rammen for arbeidet vist i fig. 175. Formatet på bildet som er plassert i det, er satt i forhold til det gylne snitt. Ytre dimensjoner rammer med samme bredde på sidene vil ikke gi den gylne proporsjonen. Derfor antas forholdet mellom lengden og bredden (ЗЗ0X220) å være litt mindre enn det gylne tallet, dvs. lik 1,5, og bredden på tverrleddene økes tilsvarende sammenlignet med sidesidene. Dette gjorde det mulig å komme frem til dimensjonene til rammen i lyset (for maleriet), noe som ga proporsjonene til det gylne snitt. Forholdet mellom bredden på rammens nedre ledd og bredden på øvre ledd justeres til et annet gyldent tall, dvs. 1,12. Dessuten er forholdet mellom bredden på den nedre lenken og bredden på sidelenken (94:63) nær 1,5 (i figuren - alternativet til venstre).

La oss nå gjøre et eksperiment: vi vil øke langsiden av rammen til 366 mm på grunn av bredden på den nedre lenken (den vil være 130 mm) (på bildet - alternativet til høyre), noe som ikke bare vil bringe forholdet nærmere, men også til gullet
nummer 1,62 i stedet for 1,12. Resultatet er en ny komposisjon som kan brukes i et annet produkt, men for rammen er det et ønske om å gjøre den kortere. Dekk den nedre delen med en linjal så mye at øyet "aksepterer" den resulterende andelen, og vi vil få lengden på 330 mm, det vil si at vi nærmer oss den originale versjonen.

Altså, analyserer ulike alternativer(det kan være andre enn de to diskuterte), mesteren slår seg på den eneste mulige løsningen fra hans synspunkt.

Det er best å bruke prinsippet om det gyldne forholdet på jakt etter den ønskede sammensetningen ved hjelp av en enkel enhet, hvis grunnleggende designdiagram er vist i fig. 176. To linjaler til denne enheten kan, roterende rundt hengsel B, danne en vilkårlig vinkel. Hvis vi for en hvilken som helst vinkelløsning deler avstanden AC i det gylne snitt med et punkt K og monterer ytterligere to linjaler: KM\\BC og KE\\AB med hengsler i punktene K, E og M, så for enhver løsning AC denne avstanden vil deles på punktet K i forhold til det gylne snitt.

Victor Lavrus

Gyldent forhold - harmonisk proporsjon

I matematikk proporsjon(lat. proportio) kaller likheten mellom to relasjoner: en : b = c : d.

Rett segment AB kan deles inn i to deler på følgende måter:

i to like deler - AB : AC = AB : Sol;

i to ulike deler på noen måte (slike deler danner ikke proporsjoner);

altså når AB : AC = AC : Sol.

Sistnevnte er den gylne divisjonen eller delingen av et segment i ekstreme og gjennomsnittlige forhold.

en : b = b : c eller Med : b = b : EN.

Ris. 1. Geometrisk bilde av det gylne snitt

Praktisk bekjentskap med det gyldne snitt begynner med å dele et rett linjesegment i den gyldne proporsjonen ved hjelp av et kompass og linjal.

Ris. 2. Dele et rett linjestykke ved hjelp av det gylne snitt. B.C. = 1/2 AB; CD = B.C.

Fra punkt I en perpendikulær lik halvparten gjenopprettes AB. Mottatt poeng MED forbundet med en linje til et punkt EN. Et segment plottes på den resulterende linjen Sol slutter med en prikk D. Linjestykke AD overført til direkte AB. Det resulterende punktet E deler et segment AB i det gylne snitt.

Egenskapene til det gylne snitt er beskrevet av ligningen:

x 2 - x - 1 = 0.

Løsning på denne ligningen:

Egenskapene til det gylne snitt har skapt en romantisk aura av mystikk og nesten mystisk tilbedelse rundt dette nummeret.

Andre gylne snitt

Det bulgarske magasinet «Fatherland» (nr. 10, 1983) publiserte en artikkel av Tsvetan Tsekov-Karandash «On the second golden section», som følger av hoveddelen og gir et nytt forhold på 44:56.

Denne andelen finnes i arkitektur, og oppstår også når man konstruerer komposisjoner av bilder av et langstrakt horisontalt format.

Ris. 3. Konstruksjon av det andre gylne snitt

Inndelingen utføres som følger (se fig. 3). Linjestykke AB delt etter det gylne snitt. Fra punkt MED perpendikulæren gjenopprettes CD. Radius AB det er et poeng D, som er forbundet med en linje til et punkt EN. Rett vinkel ACD er delt i to. Fra punkt MED en linje trekkes til den skjærer linjen AD. Punktum E deler et segment AD i forhold til 56:44.

Ris. 4.Å dele et rektangel med linjen til det andre gylne snittet

I fig. Figur 4 viser posisjonen til linjen til det andre gylne snitt. Den er plassert midt mellom den gyldne snittlinjen og midtlinjen i rektangelet.

Gylden trekant

For å finne segmenter av den gylne andelen av stigende og synkende serier, kan du bruke pentagram.

Ris. 5. Konstruksjon av en vanlig femkant og pentagram

For å bygge et pentagram, må du bygge en vanlig femkant. Metoden for konstruksjonen ble utviklet av den tyske maleren og grafikeren Albrecht Durer (1471...1528). La O- sentrum av sirkelen, EN- et punkt på en sirkel og E- midten av segmentet OA. Vinkelrett på radius OA, gjenopprettet på punktet OM, skjærer sirkelen i punktet D. Bruk et kompass til å tegne et segment på diameteren C.E. = ED. Sidelengden til en vanlig femkant innskrevet i en sirkel er DC. Legg ut segmenter på sirkelen DC og vi får fem poeng for å trekke en vanlig femkant. Vi kobler hjørnene på femkanten gjennom hverandre med diagonaler og får et femkant. Alle diagonaler i femkanten deler hverandre i segmenter forbundet med det gylne snitt.

Hver ende av den femkantede stjernen representerer en gylden trekant. Sidene danner en vinkel på 36° på toppen, og basen, lagt på siden, deler den i forholdet til det gylne snitt.

Ris. 6. Konstruksjon av den gylne trekanten

Vi gjennomfører en direkte AB. Fra punkt EN legg et segment på den tre ganger OM vilkårlig verdi, gjennom det resulterende punktet R tegne en vinkelrett på linjen AB, på vinkelrett til høyre og venstre for punktet R sett til side segmentene OM. Fikk poeng d Og d 1 koble med rette linjer til et punkt EN. Linjestykke dd sett 1 på streken Annonse 1, får et poeng MED. Hun delte linjen Annonse 1 i forhold til det gylne snitt. Linjer Annonse 1 og dd 1 brukes til å konstruere et "gyllent" rektangel.

Historien om det gylne snitt

Det er generelt akseptert at konseptet med den gylne inndelingen ble introdusert i vitenskapelig bruk av Pythagoras, en gammel gresk filosof og matematiker (VI århundre f.Kr.). Det er en antagelse om at Pythagoras lånte sin kunnskap om den gylne divisjonen fra egypterne og babylonerne. Faktisk indikerer proporsjonene til Cheops-pyramiden, templene, bas-relieffer, husholdningsartikler og smykker fra graven til Tutankhamun at egyptiske håndverkere brukte forholdene til den gylne divisjonen når de laget dem. Den franske arkitekten Le Corbusier fant at i relieffet fra tempelet til farao Seti I i Abydos og i relieffet som skildrer farao Ramses, samsvarer proporsjonene til figurene med verdiene til den gyldne divisjonen. Arkitekten Khesira, avbildet på et relieff av en treplate fra en grav oppkalt etter ham, holder i hendene måleinstrumenter der proporsjonene til den gylne inndelingen er registrert.

Ris. 7. Dynamiske rektangler

Platon (427...347 f.Kr.) visste også om den gylne inndelingen. Dialogen hans "Timaeus" er viet til de matematiske og estetiske synspunktene til den pythagorasiske skolen og spesielt til spørsmålene om den gylne divisjonen.

Ris. 8. Antikt kompass med gyldne snitt

I den gamle litteraturen som har kommet ned til oss, ble den gyldne inndelingen først nevnt i Euklids elementer. I den andre boken til "Prinsipene" er den geometriske konstruksjonen av den gyldne inndelingen gitt etter Euclid, ble studien av den gyldne inndelingen utført av Hypsicles (2. århundre f.Kr.), Pappus (III århundre e.Kr.) og andre middelalderens Europa, med den gylne inndelingen Vi møttes gjennom arabiske oversettelser av Euklids elementer. Oversetteren J. Campano fra Navarra (III århundre) kom med kommentarer til oversettelsen. Hemmelighetene til den gylne divisjonen ble nidkjært bevoktet og holdt i streng hemmelighet. De var bare kjent for innviede.

Under renessansen økte interessen for den gyldne divisjonen blant forskere og kunstnere på grunn av dens bruk i både geometri og kunst, spesielt innen arkitektur, Leonardo da Vinci, en kunstner og vitenskapsmann, så at italienske kunstnere hadde mye empirisk erfaring, men lite. kunnskap. Han ble unnfanget og begynte å skrive en bok om geometri, men på den tiden dukket det opp en bok av munken Luca Pacioli, og Leonardo forlot ideen. I følge samtidige og vitenskapshistorikere var Luca Pacioli en ekte lysmann, den største matematikeren i Italia i perioden mellom Fibonacci og Galileo. Luca Pacioli var en elev av kunstneren Piero della Franceschi, som skrev to bøker, hvorav den ene ble kalt «On Perspective in Painting». Han regnes som skaperen av beskrivende geometri.

Luca Pacioli forsto perfekt betydningen av vitenskap for kunst. I 1496, på invitasjon fra hertugen av Moreau, kom han til Milano, hvor han foreleste om matematikk. Leonardo da Vinci jobbet også i Milano ved Moro-domstolen på den tiden. I 1509 ble Luca Paciolis bok "The Divine Proportion" utgitt i Venezia med strålende utførte illustrasjoner, og det er derfor det antas at de ble laget av Leonardo da Vinci. Boken var en entusiastisk salme til det gylne snitt. Blant de mange fordelene med den gyldne proporsjon, unnlot ikke munken Luca Pacioli å navngi dens "guddommelige essens" som et uttrykk for den guddommelige treenigheten - Gud sønnen, Gud faren og Gud den hellige ånd (det ble antydet at den lille segmentet er personifiseringen av Gud sønnen, det større segmentet - Gud faren, og hele segmentet - Den Hellige Ånds Gud).

Leonardo da Vinci ga også mye oppmerksomhet til studiet av den gylne divisjonen. Han laget seksjoner av en stereometrisk kropp dannet av vanlige femkanter, og hver gang fikk han rektangler med sideforhold i den gylne inndelingen. Det er derfor han ga denne avdelingen navnet gyldne snitt. Så den er fortsatt den mest populære.

Samtidig, i Nord-Europa, i Tyskland, jobbet Albrecht Dürer med de samme problemene. Han skisserer innledningen til den første versjonen av avhandlingen om proporsjoner. Dürer skriver. «Det er nødvendig at noen som vet hvordan man gjør noe, skal lære det til andre som trenger det. Dette er hva jeg satte meg for å gjøre."

Etter et av Dürers brev å dømme møtte han Luca Pacioli mens han var i Italia. Albrecht Durer utvikler i detalj teorien om proporsjoner av menneskekroppen. Dürer tildelte det gylne snitt en viktig plass i sitt system av relasjoner. En persons høyde er delt i gylne proporsjoner av beltets linje, så vel som av en linje trukket gjennom tuppene av langfingrene på de senkede hendene, den nedre delen av ansiktet ved munnen, etc. Dürers proporsjonale kompass er velkjent.

Stor astronom på 1500-tallet. Johannes Kepler kalte det gylne snitt for en av geometriens skatter. Han var den første som gjorde oppmerksom på betydningen av den gyldne proporsjon for botanikk (plantevekst og deres struktur).

Kepler kalte den gyldne andelen selv-fortsatt "Den er strukturert på en slik måte," skrev han, "at de to laveste leddene i denne uendelige andelen summerer seg til den tredje termen, og eventuelle to siste ledd, hvis de legges sammen. , gi neste ledd, og den samme andelen forblir til uendelig."

Konstruksjonen av en serie segmenter av den gylne andelen kan gjøres både i retning av økning (økende serie) og i retning av nedgang (synkende serie).

Hvis du er på en rett linje med vilkårlig lengde, sett til side segmentet m, sett segmentet ved siden av M. Basert på disse to segmentene bygger vi en skala av segmenter av den gylne andelen av stigende og synkende serier

Ris. 9. Konstruksjon av en skala av gylne proporsjonssegmenter

I de påfølgende århundrene ble regelen om den gyldne proporsjon til en akademisk kanon, og da kampen mot akademisk rutine over tid begynte i kunsten, i kampens hete, "kastet de ut babyen med badevannet." Det gyldne snitt ble "oppdaget" igjen på midten av 1800-tallet. I 1855 publiserte den tyske forskeren av det gylne snitt, professor Zeising, sitt arbeid "Estetiske studier". Det som skjedde med Zeising var akkurat det som uunngåelig skulle skje med en forsker som vurderer et fenomen som sådan, uten sammenheng med andre fenomener. Han absoluttiserte andelen av det gylne snitt, og erklærte det universelt for alle fenomener innen natur og kunst. Zeising hadde mange tilhengere, men det var også motstandere som erklærte hans proporsjonsdoktrine for å være «matematisk estetikk».

Ris. 10. Gylne proporsjoner i deler av menneskekroppen

Zeising gjorde en kjempejobb. Han målte rundt to tusen menneskekropper og kom til den konklusjon at det gylne snitt uttrykker den gjennomsnittlige statistiske loven. Delingen av kroppen etter navlepunktet er den viktigste indikatoren på det gylne snitt. Proporsjoner mannlig kropp svinge innenfor gjennomsnittsforholdet 13: 8 = 1,625 og er noe nærmere det gyldne snitt enn proporsjonene til kvinnekroppen, i forhold til hvilken gjennomsnittsverdien av andelen er uttrykt i forholdet 8: 5 = 1,6. Hos en nyfødt er andelen 1:1, ved 13 års alder er den 1,6, og ved 21 år er den lik en mann. Proporsjonene til det gyldne snitt vises også i forhold til andre deler av kroppen - lengden på skulderen, underarmen og hånden, hånd og fingre, etc.

Ris. elleve. Gylne proporsjoner i menneskefiguren

Zeising testet gyldigheten av teorien hans på greske statuer. Han utviklet proporsjonene til Apollo Belvedere mest detaljert. Greske vaser og arkitektoniske strukturer ble undersøkt forskjellige tidsepoker, planter, dyr, fugleegg, musikalske toner, poetiske metre. Zeising ga en definisjon av det gylne snitt og viste hvordan det uttrykkes i rette linjesegmenter og i tall. Da tallene som uttrykker lengdene til segmentene ble oppnådd, så Zeising at de utgjorde en Fibonacci-serie, som kunne fortsettes i det uendelige i den ene eller den andre retningen. Hans neste bok fikk tittelen "Den gylne divisjon som den grunnleggende morfologiske loven i natur og kunst." I 1876 ble det utgitt en liten bok, nesten en brosjyre, i Russland som skisserte dette arbeidet til Zeising. Forfatteren tok tilflukt under initialene Yu.F.V. Denne utgaven nevner ikke et eneste malerverk.

I sent XIX- tidlig på 1900-tallet Mange rent formalistiske teorier dukket opp om bruken av det gylne snitt i kunstverk og arkitektur. Med utviklingen av design og teknisk estetikk utvidet loven om det gylne snitt til design av biler, møbler osv.

Fibonacci-serien

Navnet på den italienske matematikermunken Leonardo av Pisa, bedre kjent som Fibonacci (sønn av Bonacci), er indirekte forbundet med historien til det gylne snitt. Han reiste mye i øst, introduserte Europa for indiske (arabiske) tall. I 1202 ble hans matematiske verk "The Book of the Abacus" (tellebrett) utgitt, som samlet alle problemene som var kjent på den tiden. Et av problemene var "Hvor mange par kaniner vil bli født fra ett par på ett år." Etter å ha reflektert over dette emnet, bygde Fibonacci følgende serie med tall:

En serie med tall 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. kjent som Fibonacci-serien. Det særegne ved tallrekkefølgen er at hver av dens medlemmer, fra den tredje, lik summen to foregående 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 osv., og forholdet mellom tilstøtende tall i serien nærmer seg forholdet mellom den gylne divisjonen. Så, 21: 34 = 0,617 og 34: 55 = 0,618. Dette forholdet er angitt med symbolet F. Bare dette forholdet - 0,618: 0,382 - gir en kontinuerlig inndeling av et rett linjesegment i den gylne proporsjonen, øker eller reduserer det til uendelig, når det mindre segmentet er relatert til det større som det større er til helheten.

Fibonacci tok også for seg de praktiske behovene til handel: hva er det minste antallet vekter som kan brukes til å veie et produkt? Fibonacci beviser at det optimale vektsystemet er: 1, 2, 4, 8, 16...

Generalisert gyldent snitt

Fibonacci-serien kunne ha forblitt bare en matematisk hendelse, hvis ikke for det faktum at alle forskere av den gylne divisjonen i plante- og dyreverdenen, for ikke å nevne kunst, alltid kom til denne serien som et aritmetisk uttrykk for loven om det gylne. inndeling.

Forskere fortsatte å aktivt utvikle teorien om Fibonacci-tall og det gylne snitt. Yu Matiyasevich løser Hilberts 10. problem ved å bruke Fibonacci-tall. Det dukker opp elegante metoder for å løse en rekke kybernetiske problemer (søketeori, spill, programmering) ved hjelp av Fibonacci-tall og det gylne snitt. I USA opprettes til og med Mathematical Fibonacci Association, som har publisert et spesialtidsskrift siden 1963.

En av prestasjonene på dette feltet er oppdagelsen av generaliserte Fibonacci-tall og generaliserte gylne snitt.

Fibonacci-serien (1, 1, 2, 3, 5, 8) og den "binære" serien med vekter oppdaget av ham 1, 2, 4, 8, 16... ved første øyekast er helt forskjellige. Men algoritmene for deres konstruksjon er veldig like hverandre: i det første tilfellet er hvert tall summen av det forrige tallet med seg selv 2 = 1 + 1; 4 = 2 + 2..., i den andre - dette er summen av de to foregående tallene 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Er det mulig å finne en generell matematisk formel som vi får " binære serier og Fibonacci serier? Eller kanskje denne formelen vil gi oss nye tallsett, besitter noen nye unike egenskaper?

Faktisk, la oss angi den numeriske parameteren S, som kan ha alle verdier: 0, 1, 2, 3, 4, 5... Tenk på en tallserie, S+ 1 av de første leddene er enheter, og hver av de påfølgende er lik summen av to ledd av den forrige og atskilt fra den forrige med S trinn. Hvis n Vi betegner det tredje leddet i denne serien med φ S ( n), så får vi den generelle formelen φ S ( n) = φ S ( n- 1) + φ S ( n - S - 1).

Det er åpenbart at når S= 0 fra denne formelen får vi en "binær" serie, med S= 1 - Fibonacci-serien, med S= 2, 3, 4. ny serie med tall, som kalles S-Fibonacci-tall.

Generelt gyldent S-proporsjon er den positive roten til den gyldne ligningen S-seksjoner x S+1 - x S - 1 = 0.

Det er lett å vise at når S= 0, segmentet er delt i to, og når S= 1 - det kjente klassiske gylne snittet.

Forholdet mellom naboer S- Fibonacci-tall sammenfaller med absolutt matematisk nøyaktighet i grensen med gull S-proporsjoner! I slike tilfeller sier matematikere at gull S-seksjoner er numeriske invarianter S-Fibonacci-tall.

Fakta som bekrefter eksistensen av gull S-seksjoner i naturen, siterer den hviterussiske forskeren E.M. Soroko i boken "Structural Harmony of Systems" (Minsk, "Science and Technology", 1984). Det viser seg for eksempel at godt studerte binære legeringer har spesielle, uttalte funksjonelle egenskaper (termisk stabile, harde, slitesterke, oksidasjonsbestandige osv.) bare hvis egenvekt de originale komponentene er forbundet med hverandre med en av gullene S-proporsjoner. Dette tillot forfatteren å fremsette hypotesen om at gull S-seksjoner er numeriske invarianter av selvorganiserende systemer. Når den først er bekreftet eksperimentelt, kan denne hypotesen være av grunnleggende betydning for utviklingen av synergetikk – et nytt vitenskapsfelt som studerer prosesser i selvorganiserende systemer.

Bruker gullkoder S-proporsjoner kan uttrykkes med et hvilket som helst reelt tall som summen av gullkrefter S-proporsjoner med heltallskoeffisienter.

Den grunnleggende forskjellen mellom denne metoden for å kode tall er at basene til de nye kodene, som er gylne S-proporsjoner, med S> 0 viser seg å være irrasjonelle tall. Dermed ser nye tallsystemer med irrasjonelle baser ut til å sette det historisk etablerte hierarkiet av relasjoner mellom rasjonelle og irrasjonelle tall "fra topp til fot." Faktum er at naturlige tall først ble "oppdaget"; da er forholdstallene deres rasjonelle tall. Og først senere - etter oppdagelsen av inkommensurable segmenter av pytagoreerne - ble irrasjonelle tall født. For eksempel, i desimal-, quinær-, binær- og andre klassiske posisjonstallsystemer ble naturlige tall valgt som et slags grunnleggende prinsipp - 10, 5, 2 - hvorav visse regler alle andre naturlige tall, så vel som rasjonelle og irrasjonelle tall, ble konstruert.

Et slags alternativ til eksisterende notasjonsmetoder er et nytt, irrasjonelt system, som et grunnleggende prinsipp, hvis begynnelse er et irrasjonelt tall (som, husker du, er roten til det gyldne snitt-ligningen); andre reelle tall er allerede uttrykt gjennom den.

I et slikt tallsystem kan evt naturlig tall alltid representert som endelig - og ikke uendelig, som tidligere antatt! - summen av gradene til noe av gullet S-proporsjoner. Dette er en av grunnene til at "irrasjonell" aritmetikk, med fantastisk matematisk enkelhet og eleganse, ser ut til å ha absorbert beste kvaliteter klassisk binær og Fibonacci-aritmetikk.

Prinsipper for dannelse i naturen

Alt som tok en eller annen form ble dannet, vokste, strebet etter å ta plass i rommet og bevare seg selv. Dette ønsket realiseres hovedsakelig i to alternativer - å vokse oppover eller spre seg over jordens overflate og vri seg i en spiral.

Skallet er vridd i en spiral. Bretter du den ut får du en lengde litt kortere enn lengden på slangen. Et lite ti-centimeters skall har en spiral på 35 cm. Spiraler er svært vanlige i naturen. Ideen om det gylne snitt vil være ufullstendig uten å snakke om spiralen.

Ris. 12. Arkimedes spiral

Formen på det spiralkrøllede skallet tiltrakk seg oppmerksomheten til Archimedes. Han studerte det og kom opp med en ligning for spiralen. Spiralen tegnet i henhold til denne ligningen kalles ved hans navn. Økningen i trinnet hennes er alltid jevn. For tiden er Archimedes-spiralen mye brukt i teknologi.

Goethe la også vekt på naturens tendens til spiralitet. Det spiralformede og spiralformede arrangementet av blader på tregrener ble lagt merke til for lenge siden. Spiralen ble sett i arrangementet av solsikkefrø, kongler, ananas, kaktus, etc. Botanikernes og matematikernes felles arbeid har belyst disse fantastiske fenomener natur. Det viste seg at Fibonacci-serien manifesterer seg i arrangementet av blader på en gren (phylotaxis), solsikkefrø og furukongler, og derfor manifesterer loven om det gylne snitt seg. Edderkoppen vever nettet sitt i et spiralmønster. En orkan snurrer som en spiral. Skremt flokk reinsdyr spiraler bort. DNA-molekylet er vridd i en dobbel helix. Goethe kalte spiralen «livets kurve».

Blant urtene langs veien vokser en umerkelig plante - sikori. La oss se nærmere på det. Et skudd har dannet seg fra hovedstammen. Det første bladet lå akkurat der.

Ris. 1. 3. Sikori

Skuddet gjør et kraftig utkast ut i rommet, stopper, slipper et blad, men denne gangen er det kortere enn det første, gjør igjen et utkast ut i rommet, men med mindre kraft, slipper ut et blad av en enda mindre størrelse og skytes ut igjen . Hvis det første utslippet tas som 100 enheter, er det andre lik 62 enheter, det tredje - 38, det fjerde - 24, etc. Lengden på kronbladene er også underlagt den gyldne proporsjonen. I å vokse og erobre plass opprettholdt planten visse proporsjoner. Vekstimpulsene avtok gradvis i forhold til det gylne snitt.

Ris. 14. Viviparøs øgle

Ved første øyekast har øglen proporsjoner som er behagelige for øynene våre - lengden på halen er relatert til lengden på resten av kroppen som 62 til 38.

Både i plante- og dyreverdenen bryter naturens dannelsestendens vedvarende gjennom - symmetri om vekstretning og bevegelsesretning. Her vises det gylne snitt i proporsjonene av deler vinkelrett på vekstretningen.

Naturen har gjennomført inndeling i symmetriske deler og gylne proporsjoner. Delene avslører en repetisjon av strukturen i helheten.

Ris. 15. fugleegg

Den store Goethe, en poet, naturforsker og kunstner (han tegnet og malte i akvareller), drømte om å skape en enhetlig doktrine om form, dannelse og transformasjon av organiske kropper. Det var han som introduserte begrepet morfologi i vitenskapelig bruk.

Pierre Curie formulerte på begynnelsen av dette århundret en rekke dyptgripende ideer om symmetri. Han hevdet at man ikke kan vurdere symmetrien til noen kropp uten å ta hensyn til miljøets symmetri.

Mønstrene til "gylden" symmetri manifesteres i energioverganger elementære partikler, i strukturen til noen kjemiske forbindelser, i planetariske og kosmiske systemer, i genstrukturene til levende organismer. Disse mønstrene, som angitt ovenfor, eksisterer i strukturen til individuelle menneskelige organer og kroppen som helhet, og manifesterer seg også i biorytmene og funksjonen til hjernen og visuell persepsjon.

Gyldent snitt og symmetri

Det gylne snitt kan ikke vurderes alene, separat, uten sammenheng med symmetri. Den store russiske krystallografen G.V. Wulf (1863...1925) anså det gylne snitt for å være en av manifestasjonene av symmetri.

Den gyldne divisjonen er ikke en manifestasjon av asymmetri, noe motsatt av symmetri I følge moderne ideer er den gyldne divisjon asymmetrisk symmetri. Vitenskapen om symmetri inkluderer slike begreper som statisk Og dynamisk symmetri. Statisk symmetri kjennetegner fred og balanse, mens dynamisk symmetri kjennetegner bevegelse og vekst. I naturen er statisk symmetri således representert av strukturen til krystaller, og i kunsten karakteriserer den fred, balanse og immobilitet. Dynamisk symmetri uttrykker aktivitet, karakteriserer bevegelse, utvikling, rytme, det er bevis på liv. Statisk symmetri er preget av like segmenter og like verdier. Dynamisk symmetri er preget av en økning i segmenter eller deres reduksjon, og det uttrykkes i verdiene til det gyldne snitt i en økende eller avtagende serie.

Gylne proporsjoner i litteraturen. Poesi og det gylne snitt

Mye i strukturen til poetiske verk gjør at denne kunstformen ligner på musikk. En klar rytme, en naturlig veksling av stressede og ubetonede stavelser, en ordnet meter med dikt, og deres følelsesmessige rikdom gjør poesi søster musikalske verk. Hvert vers har sin egen musikalske form - sin egen rytme og melodi. Man kan forvente at i diktstrukturen vil noen trekk ved musikalske verk, lovene for musikalsk harmoni, og følgelig den gyldne proporsjonen vises.

La oss starte med størrelsen på diktet, det vil si antall linjer i det. Det ser ut til at denne parameteren i diktet kan endres vilkårlig. Det viste seg imidlertid at dette ikke var tilfelle. For eksempel N. Vasyutinskys analyse av diktene til A.S. Pushkin fra dette synspunktet viste at størrelsene på dikt er fordelt veldig ujevnt; det viste seg at Pushkin klart foretrekker størrelsene 5, 8, 13, 21 og 34 linjer (Fibonacci-tall).

Mange forskere har lagt merke til at dikt ligner på musikkstykker; de har også kulmineringspunkter som deler diktet i forhold til det gylne snitt. Tenk for eksempel på diktet av A.S. Pushkins "Skomaker":

En skomaker så en gang opp etter maleriet
Og han påpekte feilen i skoene;
Kunstneren tok umiddelbart opp børsten og korrigerte seg selv,
Så, med armene akimbo, fortsatte skomakeren:
"Jeg synes ansiktet er litt skjevt...
Er ikke disse brystene for nakne?
Her avbrøt Apelles utålmodig:
"Døm, min venn, ikke høyere enn støvelen!"

jeg har en venn hold øye med:
Jeg vet ikke hvilket fag han er i
Han var en ekspert, selv om han var streng i ord,
Men djevelen hater ham for å dømme verden:
Prøv å dømme støvler!

La oss analysere denne lignelsen. Diktet består av 13 linjer. Den har to semantiske deler: den første på 8 linjer og den andre (lignelsens moral) på 5 linjer (13, 8, 5 er Fibonacci-tall).

Et av Pushkins siste dikt, "I value loud rights not dearly..." består av 21 linjer og har to semantiske deler: 13 og 8 linjer.

Jeg verdsetter ikke høylytte rettigheter høyt,
Noe som får mer enn ett hode til å snurre.
Jeg klager ikke på at gudene nektet
Det er min søte skjebne å utfordre skatter
Eller hindre konger i å kjempe mot hverandre;
Og det er ikke nok for meg å bekymre meg om pressen er fri
Dumme idioter, eller sensitiv sensur
I magasinplaner er jokeren flau.
Alt dette, skjønner du, er ord, ord, ord.
Andre, bedre rettigheter er kjære for meg:
Jeg trenger en annen, bedre frihet:
Avhengig av kongen, avhengig av folket -
Bryr vi oss? Gud være med dem.
Ingen
Ikke gi en rapport, bare til deg selv
Å tjene og behage; for kraft, for livery
Ikke bøy samvittigheten, tankene, nakken;
Å vandre her og der etter eget ønske,
Å beundre naturens guddommelige skjønnhet,
Og før kreasjonene av kunst og inspirasjon
Skjelver av glede i ømhetens henrykkelse,
Hvilken lykke! Det er riktig...

Det er karakteristisk at den første delen av dette verset (13 linjer), i henhold til dets semantiske innhold, er delt inn i 8 og 5 linjer, det vil si at hele diktet er strukturert i henhold til lovene i den gylne proporsjonen.

Analysen av romanen "Eugene Onegin" laget av N. Vasyutinsky er av utvilsomt interesse. Denne romanen består av 8 kapitler, hver med et gjennomsnitt på rundt 50 vers. Det åttende kapittelet er det mest perfekte, mest polerte og følelsesmessig rike. Den har 51 vers. Sammen med Eugenes brev til Tatiana (60 linjer), samsvarer dette nøyaktig med Fibonacci-tallet 55!

N. Vasyutinsky uttaler:

"Kulminasjonen av kapitlet er Eugenes kjærlighetserklæring til Tatyana - linjen "Å bli blek og visne bort ... dette er lykke!" Denne linjen deler hele det åttende kapittelet i to deler - i den første er det 477 linjer, og i den andre - 295 linjer er 1,617. Den fineste korrespondanse til verdien av den gyldne proporsjon.

Lermontovs berømte dikt "Borodino" er delt i to deler: en introduksjon rettet til fortelleren og opptar bare én strofe ("Fortell meg, onkel, det er ikke uten grunn ..."), og hoveddel, som representerer en uavhengig helhet som deler seg i to like deler. Den første av dem beskriver forventningen til kampen med økende spenning, den andre beskriver selve kampen med en gradvis nedgang i spenningen mot slutten av diktet. Grensen mellom disse delene er verkets kulminasjonspunkt og faller nøyaktig ved inndelingen av det gylne snitt.

Hoveddelen av diktet består av 13 syvlinjers linjer, det vil si 91 linjer. Etter å ha delt det med det gyldne snitt (91:1.618 = 56.238), er vi overbevist om at delingspunktet er i begynnelsen av det 57. verset, der det er en kort setning: "Vel, det var en dag!". Det er denne frasen som representerer "kulminasjonspunktet for spent forventning", fullfører den første delen av diktet (forventning av slaget) og åpner den andre delen (beskrivelse av slaget).

Dermed spiller det gyldne snitt en veldig meningsfull rolle i poesi, og fremhever diktets klimaks.

Gyldent snitt i arkitektur, skulptur, maleri, fotografi

Et av de vakreste verkene i gammel gresk arkitektur er Parthenon (5. århundre f.Kr.).

Figurene viser en rekke mønstre knyttet til det gylne snitt. Proporsjonene til bygningen kan uttrykkes gjennom forskjellige potenser av tallet Ф=0,618...

På planløsningen til Parthenon kan du også se de "gyldne rektanglene":

Vi kan se det gylne snitt i katedralbygningen Notre Dame i Paris(Notre Dame de Paris), og i Cheops-pyramiden:

Proporsjonene til Cheops-pyramiden, templene, basrelieffer, husholdningsartikler og smykker fra graven til Tutankhamun indikerer at egyptiske håndverkere brukte forholdene til den gylne divisjonen når de laget dem. Den franske arkitekten Le Corbusier fant at i relieffet fra tempelet til farao Seti I i Abydos og i relieffet som skildrer farao Ramses, samsvarer proporsjonene til figurene med verdiene til den gyldne divisjonen. Arkitekten Khesira, avbildet på et relieff av en treplate fra en grav oppkalt etter ham, holder i hendene måleinstrumenter der proporsjonene til den gylne inndelingen er registrert.

Når det gjelder pyramidene, ble ikke bare de egyptiske pyramidene bygget i samsvar med de perfekte proporsjonene til det gylne snitt; det samme fenomenet ble funnet i de meksikanske pyramidene. Tverrsnittet av pyramiden viser en form som ligner på en trapp. Det første laget har 16 trinn, det andre 42 trinn og det tredje - 68 trinn.
Disse tallene er basert på Fibonacci-forholdet som følger:

16 x 1,618 = 26

26 x 1,618 = 42

Arkitekturen til St. Basil's Cathedral har mange gylne proporsjoner:

Den gyldne proporsjonen ble brukt av mange gamle skulptører. Den gyldne andelen av statuen av Apollo Belvedere er kjent: Høyden til den avbildede mannen er delt av navlelinjen i det gylne snitt.

Tilbake i renessansen oppdaget kunstnere at ethvert bilde har visse punkter som ufrivillig vekker vår oppmerksomhet, de såkalte visuelle sentrene. I dette tilfellet spiller det ingen rolle hvilket format bildet har - horisontalt eller vertikalt. Det er kun fire slike punkter de deler bildestørrelsen horisontalt og vertikalt i det gylne snitt, dvs. de er plassert i en avstand på omtrent 3/8 og 5/8 fra de tilsvarende kantene av planet.

Denne oppdagelsen ble kalt det "gyldne forholdet" av maleriet av kunstnere på den tiden. Derfor, for å trekke oppmerksomhet til hovedelementet i fotografiet, er det nødvendig å kombinere dette elementet med et av de visuelle sentrene.

På bildet I.I. Shishkins "Ship Grove" viser motiver av det gylne snitt. Et sterkt solbelyst furutre (stående i forgrunnen) deler lengden på maleriet omtrent i det gylne snitt. Til høyre for furutreet er en solbelyst ås. Den deler høyre side av bildet horisontalt i det gylne snitt. Til venstre for hovedfuruen er det mange furu - hvis ønskelig, kan du fortsette å dele bildet i proporsjonene til det gylne snittet.

Tilstedeværelsen i bildet av lyse vertikaler og horisontaler, som deler det i forhold til det gylne snitt, gir det en karakter av balanse og ro, i samsvar med kunstnerens intensjon. Når en kunstner lager et bilde med raskt utviklende handling, blir et slikt geometrisk komposisjonsskjema (med en overvekt av vertikaler og horisontale) uakseptabelt.

Følelsen av dynamikk og spenning viser seg kanskje sterkest i en annen enkel geometrisk figur- spiraler. Multifigurkomposisjonen, utført i 1509 - 1510 av Raphael, da den berømte maleren skapte sine fresker i Vatikanet, utmerker seg ved dynamikken og dramatikken i handlingen. Raphael fullførte aldri planen sin, men skissen hans ble gravert av den ukjente italienske grafikeren Marcantinio Raimondi, som basert på denne skissen laget graveringen "Massacre of the Innocents".

Hvis vi i Raphaels forberedende skisse mentalt tegner linjer som går fra det semantiske sentrum av komposisjonen - punktet der krigerens fingre lukket seg rundt barnets ankel - langs figurene til barnet, kvinnen som holder ham inntil, krigeren med sverdet. hevet, og deretter langs figurene av samme gruppe på de høyre delene av skissen (i figuren er disse linjene tegnet i rødt), og koble deretter disse brikkene med en buet stiplet linje, og med meget stor nøyaktighet er en gylden spiral oppnådd. Dette kan kontrolleres ved å måle forholdet mellom lengdene til segmentene kuttet av en spiral på rette linjer som går gjennom begynnelsen av kurven.

Det er ukjent om Raphael faktisk tegnet den gyldne spiralen da han laget komposisjonen "Massacre of the Innocents" eller bare "følte" den. Imidlertid kan vi med sikkerhet si at gravøren Raimondi så denne spiralen. Dette er bevist av de nye elementene i komposisjonen han la til, og understreker reverseringen av spiralen på de stedene der den bare er indikert med en stiplet linje. Disse elementene kan sees i Raimondis siste gravering: buen på broen som strekker seg fra kvinnens hode er på venstre side av komposisjonen og den tilbakelente kroppen til barnet er i midten.

Går vi videre til eksempler på det "gyldne snittet" i maleri, kan man ikke unngå å fokusere på arbeidet til Leonardo da Vinci. La oss se nøye på maleriet "La Gioconda". Sammensetningen av portrettet er basert på "gyldne trekanter".

Moderne modellvirksomhet bruker også ideelle proporsjoner, fordi "alt nytt er godt glemt gammelt":

Informasjonskilder:

Kovalev F.V. Gyldent snitt i maleri. K.: Vyshcha skole, 1989.

Kepler I. Om sekskantede snøfnugg. - M., 1982.

Durer A. Dagbøker, brev, avhandlinger - L., M., 1957.

Tsekov-Karandash Ts. Om det andre gyldne snitt. - Sofia, 1983.

Stakhov A. Koder for den gylne proporsjon.

Ved å kutte en firkant med side a fra et rektangel bygget etter prinsippet om det gylne snitt, får vi et nytt, mindre rektangel med samme egenskap

gylden seksjon (gylden proporsjon, deling i ekstreme og gjennomsnittlige forhold, harmonisk divisjon, Phidias-tall) - deling av en kontinuerlig verdi i deler i et slikt forhold der den største delen er relatert til den mindre som hele verdien er til den større. For eksempel å dele et segment AC i to deler på en slik måte at det meste AB refererer til den mindre Sol akkurat som hele segmentet AC refererer til AB(dvs. | AB| / |Sol| = |AC| / |AB|).

Denne andelen er vanligvis betegnet Gresk bokstavϕ (betegnelsen τ finnes også). Det er lik:

Formelen for "gyldne harmonier", som gir tallpar som tilfredsstiller andelen ovenfor:

Når det gjelder et tall, parameteren m = 1.

I den gamle litteraturen som har kommet ned til oss, er inndelingen av et segment i ekstreme og gjennomsnittlige forhold (ἄκρος καὶ μέσος λόγος ) først funnet i Euklids elementer (ca. 300 f.Kr.), hvor den brukes til å konstruere en vanlig femkant.

C erbegrepet "gyldent snitt" (tysk)goldener Schnitt) ble introdusert av den tyske matematikeren Martin Ohm i 1835.

Matematiske egenskaper

Gyldent snitt i en femspiss stjerne

— irrasjonell algebraisk tall, positiv løsning av en av følgende ligninger

representert ved en fortsatt brøk

Til hvis passende brøker er forholdet mellom påfølgende Fibonacci-tall. Dermed, .

I en vanlig femspiss stjerne er hvert segment delt med et segment som skjærer det i det gylne snitt (det vil si forholdet mellom det blå segmentet og det grønne, så vel som det røde til blått, samt det grønne til fiolette , er like).

Konstruksjon av det gylne snitt

Her er en annen visning:

Geometrisk konstruksjon

Gyldent snitt av et segment AB kan konstrueres som følger: ved punktet B vinkelrett på AB, legg et segment på den B.C., lik halvparten AB, på segmentet A.C. sette til side et segment AD, lik A.C. − C.B., og til slutt på segmentet AB sette til side et segment A.E., lik AD. Deretter

Gyldent snitt og harmoni

Det er generelt akseptert at gjenstander som inneholder det "gyldne snittet" blir oppfattet av folk som de mest harmoniske. Proporsjonene til Cheops-pyramiden, templene, bas-relieffer, husholdningsartikler og smykker fra graven til Tutankhamon indikerer angivelig at egyptiske håndverkere brukte forholdene til det gylne snitt når de laget dem. Arkitekten Le Corbusier "fant" at i relieffet fra tempelet til farao Seti I i Abydos og i relieffet som skildrer farao Ramses, samsvarer proporsjonene til figurene med verdiene til det gylne snitt. Arkitekten Khesira, avbildet på relieffet av en treplate fra graven oppkalt etter ham, holder i hendene måleinstrumenter der proporsjonene til det gylne snittet er registrert. Fasaden til det gamle greske tempelet i Parthenon har gylne proporsjoner. Under utgravningene ble det oppdaget kompass som ble brukt av arkitekter og skulptører fra den antikke verden. Det pompeianske kompasset (museet i Napoli) inneholder også proporsjonene til den gylne inndelingen osv. osv.

"Gyldent snitt" i kunst

Gyldent snitt og visuelle sentre

Fra og med Leonardo da Vinci brukte mange kunstnere bevisst proporsjonene i det gyldne snitt.

Det er kjent at Sergei Eisenstein kunstig konstruerte filmen Battleship Potemkin i henhold til reglene for det "gyldne forholdet". Han delte båndet i fem deler. for det første tre handlinger utfolder seg på skipet. I de to siste - i Odessa, hvor opprøret utspiller seg. Denne overgangen til byen skjer nøyaktig ved det gylne snitt. Og hver del har sin egen brudd, som oppstår i henhold til loven om det gylne snitt. I en ramme, scene, episode er det et visst sprang i utviklingen av temaet: plot, stemning. Eisenstein mente at siden en slik overgang er nær det gylne snitt, blir den oppfattet som den mest logiske og naturlige.

Et annet eksempel på bruken av Golden Ratio-regelen i kinematografi er plasseringen av hovedkomponentene i rammen på spesielle punkter - "visuelle sentre". Ofte brukes fire punkter, plassert i avstander på 3/8 og 5/8 fra de tilsvarende kantene på flyet.

Det skal bemerkes at i eksemplene ovenfor dukket den omtrentlige verdien av "det gylne snittet" opp: det er lett å verifisere at verken 3/2 eller 5/3 er lik verdien av det gyldne snitt.

Den russiske arkitekten Zholtovsky brukte også det gylne snitt.

Kritikk av det gylne snitt

Det er oppfatninger om at betydningen av det gylne snitt i kunst, arkitektur og natur er overdrevet og er basert på feilaktige beregninger.

Når man diskuterer de optimale sideforhold for rektangler (papirstørrelser A0 og multipler, fotografiske platestørrelser (6:9, 9:12) eller filmrammer (ofte 2:3), film- og TV-skjermstørrelser - for eksempel 3:4 eller 9:16) en rekke alternativer ble testet. Det viste seg at de fleste oppfatter ikke gull seksjonen som optimal og anser proporsjonene som "for langstrakte."

Antall leste: 8113