Hvem skabte det gyldne snit. Gyldne proportioner i litteraturen

Kandidat for tekniske videnskaber V. BELYANIN, førende forsker ved det russiske forskningscenter "Kurchatov Institute", E. ROMANOVA, studerende ved MADI (GTU)

Videnskab og liv // Illustrationer

Det gyldne snit bliver ikke undervist i skolen. Og da en af forfatterne til artiklen foreslået nedenfor (Candidate of Technical Sciences V. Belyanin) talte om det gyldne snit til en ansøger, der planlagde at gå ind i MADI, i færd med at forberede sig til eksamen på instituttet, opstod problemet uventet stor interesse og en masse spørgsmål, som blev besvaret "på stedet", der var ingen svar. Vi besluttede at lede efter dem sammen, og så blev der opdaget finesser i det gyldne snit, som tidligere havde undgået forskere. Fælles kreativitet har ført til arbejde, der endnu en gang bekræfter de unges kreative evner og giver håb om, at videnskabens sprog ikke går tabt.

Matematikkens mønstre, ligesom en kunstners mønstre eller en digters mønstre, skal være smukke; Idéer, som farver eller ord, skal kombineres harmonisk. Skønhed er det første kriterium: der er ikke plads i verden til grim matematik.
J.H. Hardy

skønhed matematisk problem tjener som et af de vigtigste incitamenter for dens endeløse udvikling og årsagen til genereringen af adskillige applikationer. Nogle gange går der ti, hundreder og nogle gange tusinder af år, men folk finder igen og igen uventede drejninger i en velkendt løsning og dens fortolkning. Et af disse langlivede og fascinerende problemer viste sig at være problemet med det gyldne snit (GR), der afspejlede elementerne af nåde og harmoni i verden omkring os. Det er i øvrigt værd at huske på, at selvom selve andelen var kendt af Euclid, blev udtrykket "gyldne snit" introduceret af Leonardo da Vinci (se "Videnskab og liv").

Geometrisk indebærer det gyldne snit, at et segment opdeles i to ulige dele, således at den største del er den gennemsnitlige proportional mellem hele segmentet og den mindre del (fig. 1).

Algebraisk udtrykkes dette som følger:

Undersøgelsen af denne andel, selv før dens løsning viser, at mellem segmenterne -en Og b Der er mindst to overraskende forhold. For eksempel kan man fra proportion (1) nemt få udtrykket

som sætter forholdet mellem segmenterne -en, b, deres forskel og sum. Derfor kan vi sige forskelligt om det gyldne snit: to segmenter er i et harmonisk forhold, hvis deres forskel relaterer sig til det mindre segment, som det større segment relaterer til deres sum.

Den anden relation opnås, hvis det oprindelige segment tages lig med én: -en + b= 1, som meget ofte bruges i matematik. I dette tilfælde

-en 2 - b 2 = -en - b = ab.

Af disse resultater følger to overraskende sammenhænge mellem segmenterne EN Og b:

-en 2 - b 2 = -en - b = ab,(2)

som vil blive brugt i fremtiden.

Lad os nu gå videre til løsning af proportion (1). I praksis bruges to muligheder.

1. Lad os betegne forholdet -en/b igennem. Så får vi ligningen

x 2 - x - 1 = 0, (3)

Normalt betragtes kun den positive rod x 1, hvilket giver en enkel og visuel opdeling af et segment i et givet forhold. Faktisk, hvis vi tager hele segmentet som ét, så bruger vi værdien af denne rod x 1, får vi -en ≈ 0,618,b≈ 0,382.

Det er den positive rod x 1 i ligning (3) kaldes oftest gyldne snit eller andel af det gyldne snit. Den tilsvarende geometriske opdeling af et segment kaldes gyldne snit(prik MED i fig. 1).

For at lette yderligere præsentation, lad os betegne x 1 = D. Der er stadig ingen almindeligt accepteret betegnelse for det gyldne snit. Dette skyldes tilsyneladende, at det nogle gange forstås som et andet tal, hvilket vil blive diskuteret nedenfor.

Den negative rod, efterladt til side som normalt x 2 fører til en mindre klar opdeling af segmentet i to ulige dele. Pointen er, at det giver et skillepunkt MED, som ligger uden for segmentet (den såkaldte eksterne opdeling). Faktisk, hvis -en + b= 1, og derefter bruge roden x 2, får vi -en ≈ -1,618, b≈ 2.618. Derfor segmentet -en skal lægges i negativ retning (fig. 2).

2. Den anden mulighed for at løse proportion (1) er ikke grundlæggende forskellig fra den første. Vi antager ukendt forhold b/-en og betegne det med y. Så får vi ligningen

y 2 + y -1 = 0 , (4)

som har irrationelle rødder

Hvis -en + b= 1, og derefter bruge roden y 1, får vi -en = y 1 ≈ 0,618, b≈ 0,382. For roden y 2 får vi -en ≈ -1,618, b≈ 2.618. Geometrisk opdeling af et segment i forhold til det gyldne snit ved hjælp af rødder y 1 og y 2 er fuldstændig identisk med den tidligere version og svarer til fig. 1 og 2.

Positiv rod y 1 giver direkte den ønskede løsning på problemet, og kaldes også gyldne snit .

For nemheds skyld angiver vi værdien af roden y 1 = d.

I litteraturen er den gyldne proportion således matematisk udtrykt ved tallet D 1.618 eller nummer d 0,618, mellem hvilke der er to fantastiske forhold:

Dd= 1 og D - d = 1. (5)

Det er blevet bevist, at der ikke findes andre lignende talpar, der har disse egenskaber.

Ved at bruge begge notationer for det gyldne forhold skriver vi løsningerne til ligningerne (3) og (4) i symmetrisk form: = D, = -d, = d, = -D.

De usædvanlige egenskaber ved det gyldne snit er beskrevet tilstrækkeligt detaljeret i litteraturen. De er så fantastiske, at de har fanget mange fremragende tænkeres sind og skabt en aura af mystik omkring dem.

Den gyldne proportion findes i konfigurationen af planter og mineraler, strukturen af dele af universet og den musikalske skala. Det afspejler naturens globale principper, der gennemsyrer alle niveauer af organisering af levende og livløse genstande. Det bruges i arkitektur, skulptur, maleri, videnskab, computerteknologi og i design af husholdningsartikler. Kreationer, der bærer konfigurationen af det gyldne snit, fremstår proportionale og konsistente, er altid en fryd for øjet, og matematisk sprog Den gyldne proportion er ikke mindre yndefuld og elegant.

Ud over ligheder (5) fra relation (2) kan vi skelne mellem tre interessante relationer, der har en vis perfektion og ser ret attraktive og æstetisk tiltalende ud:

(6)

Naturens storhed og dybde kan ikke kun mærkes, for eksempel, når man betragter stjerner eller bjergtoppe, men også ved at kigge på nogle fantastiske formler, der er meget værdsat af matematikere for deres skønhed. Disse omfatter de elegante forhold i den gyldne proportion, den fantastiske Euler-formel e iπ = -1 (hvor jeg= √-1), formlen, der definerer det berømte Napier-tal (grundlaget for naturlige logaritmer): e = lim(1 + 1/ n) n = 2,718 at n→ ∞ og mange andre.

Efter at have løst proportion (1) virker dens idé ret simpel, men som det ofte er tilfældet med mange mennesker, ved første øjekast simple opgaver, der er mange finesser gemt i det. En af disse bemærkelsesværdige finesser, som forskerne hidtil har overset, er forbindelsen mellem rødderne af ligning (3) og (4) med vinklerne i tre bemærkelsesværdige trekanter.

For at se dette skal du overveje, hvordan et endimensionelt linjestykke, opdelt i forholdet til det gyldne snit, let kan omdannes til et todimensionelt billede i form af en trekant. For at gøre dette skal du først bruge fig. 1, læg til side på segmentet AB segmentets længde -en to gange - fra punktet EN mod punktet I og omvendt fra punktet I til siden EN. Vi får to point MED 1 og MED 2 deler segmentet AB fra forskellige ender i forhold til det gyldne snit (fig. 3). Tæller lige store segmenter AC 1 og Sol 2 radier, og punkterne EN Og I centre af cirklerne, tegn to buer, indtil de skærer hinanden i det øverste punkt MED. Forbindelse af prikkerne EN Og MED, og I Og MED, får vi en ligebenet trekant ABC med parterne AB = -en + b = 1, AC = = sol = -en = d≈ 0,618. Størrelsen af vinklerne ved hjørnerne EN Og I lad os betegne α, i toppunktet MED- β. Lad os beregne disse vinkler.

Ved cosinussætningen

(AB) 2 = 2(AC) 2 (1 - cos p).

Erstatning af de numeriske værdier af segmenterne AB Og AC ind i denne formel, får vi

På samme måde får vi

(8)

Fremkomsten af den gyldne proportion i et todimensionalt billede gjorde det muligt at forbinde rødderne af ligning (3) og (4) med vinklerne i en trekant ABC, som kan kaldes den første trekant i det gyldne snit.

Lad os udføre en lignende konstruktion ved hjælp af fig. 2. Hvis på fortsættelsen af segmentet AB udskyde fra punkt I til højre et segment svarende til segmentet -en, og roter rundt om centrene EN Og I op ad begge segmenter som radier, indtil de rører hinanden, får vi anden trekant gyldne snit(Fig. 4) . I denne ligebenede trekant er siden AB = -en + b= 1, side AC = Sol = D≈1,618, og derfor får vi ved hjælp af formlen for cosinussætningen

(9)

Vinkel a ved toppunktet MED er lig med 36 o og er relateret til den gyldne proportion ved relation (8). Som i det foregående tilfælde er vinklerne i denne trekant relateret til rødderne af ligning (3) og (4).

Den anden trekant af den gyldne proportion tjener som hovedbestanddelen af en regulær konveks femkant og sætter proportionerne af en regulær stjerneformet femkant (pentagram), hvis egenskaber er beskrevet i detaljer i bogen.

En stjerneformet femkant er en symmetrisk figur, og på samme tid vises den asymmetriske gyldne proportion i forholdet mellem dens segmenter. En sådan kombination af modsætninger tiltrækker altid med sin dybe enhed, hvis viden tillader en at trænge ind i naturens skjulte love og forstå deres enestående dybde og harmoni. Pythagoræerne, fanget af konsonansen af segmenterne i den stjerneformede femkant, valgte det som et symbol på deres videnskabelige samfund.

Siden astronomen I. Keplers tid (XVII århundrede) er der nogle gange blevet udtrykt forskellige synspunkter vedrørende, hvad der er mere fundamentalt - Pythagoras sætning eller den gyldne proportion. Pythagoras sætning ligger til grund for matematikken, den er en af dens hjørnesten. Gyldent snit ligger til grund for universets harmoni og skønhed. Ved første øjekast er det ikke svært at forstå og har ikke væsentlig grundighed. Nogle af dens uventede og dybe egenskaber er dog først for nylig blevet realiseret, hvilket tyder på behovet for at respektere dens skjulte finesse og mulige alsidighed. Pythagoras sætning og den gyldne proportion i deres udvikling er tæt sammenflettet med hinanden og med geometriske og algebraiske egenskaber. Der er ingen forskel eller grundlæggende forskel mellem dem. De konkurrerer ikke, de har forskellige formål.

Det er meget muligt, at begge synspunkter er ens, da der er en retvinklet trekant, der indeholder forskellige træk ved den gyldne proportion. Med andre ord er der en geometrisk figur, der ganske fuldstændigt kombinerer to fantastiske matematiske fakta - Pythagoras sætning og det gyldne snit.

For at konstruere en sådan trekant er det nok at forlænge siden Sol trekant ABC(Fig. 4) indtil krydset ved punktet E med vinkelret gendannet på punktet EN til siden AB(Fig. 5).

I en indre ligebenet trekant ES vinkel φ (vinkel ES) er lig med 144°, og vinklen ψ (vinkler ØK Og AES) er lig med 18 o. Side AC = SE = NE = D. Ved hjælp af Pythagoras sætning er det let at finde ud af, at længden af benet

Ved at bruge dette resultat kommer vi nemt frem til sammenhængen

Så der er fundet en direkte forbindelse af roden y 2 ligninger (4) - den sidste af rødderne af ligning (3) og (4) - med en vinkel på 144 o. I denne henseende trekanten ES kan kaldes den tredje trekant i det gyldne snit.

Hvis i en vidunderlig retvinklet trekant AVE tegne vinkelhalveringslinjen CAB indtil den skærer med siden EV på punktet F, så vil vi se det langs siden AB der er fire vinkler: 36 o, 72 o, 108 o og 144 o, som rødderne til de gyldne proportionsligninger er direkte forbundet med (relationer (7) - (10)). Således indeholder den præsenterede retvinklede trekant hele galaksen af ligesidede trekanter, der har det gyldne snit. Derudover er det ret bemærkelsesværdigt, at der på hypotenusen er to segmenter EU= D Og CF= 1,0 er i forhold til det gyldne snit med FВ = d. Vinklen ψ er relateret til rødderne D Og d ligning (3) og (4) ved relationerne

Konstruktionerne af ligebenede trekanter præsenteret ovenfor, hvis vinkler er forbundet med rødderne af ligningerne for den gyldne proportion, er baseret på det oprindelige segment AB og dens dele -en Og b. Men det gyldne snit giver dig mulighed for at modellere ikke kun trekanter beskrevet ovenfor, men også forskellige andre geometriske figurer, der bærer elementer af harmoniske forhold.

Lad os give to eksempler på sådanne konstruktioner. I det første skal du overveje segmentet AB, vist i fig. 1. Lad pointen MED- cirkelcentrum, segment b- radius. Lad os tegne en radius b cirkel og tangenter til den fra et punkt EN(Fig. 6). Lad os forbinde tangentpunkterne E Og F med en prik MED. Resultatet er en asymmetrisk rombe AECF, hvor diagonalen AC deler det i to lige store trekanter ES Og ACF.

Lad os være mere opmærksomme på en af dem, for eksempel en trekant ES. I denne trekant vinklen AES- lige linje, hypotenusen AC = -en, ben SE = b og ben AE = √ab≈ 0,486, hvilket følger af relation (2). Derfor ben AE er den geometriske middelværdi (proportional) mellem segmenterne -en Og b, det vil sige udtrykker det geometriske symmetricentrum mellem tal -en≈ 0,618 og b ≈ 0,382.

Lad os finde vinklerne på denne trekant:

Som i tidligere tilfælde er vinklerne δ og ε relateret gennem cosinus til rødderne af ligning (3) og (4).

Bemærk, at en asymmetrisk rhombus ligner en rhombus AECF, fås ved at tegne tangenter fra punktet I til en cirkel med radius -en og centreret i punktet EN.

Asymmetrisk rombe AECF opnået på en anden måde i bogen, når man analyserer dannelses- og vækstfænomenerne i den levende natur. retvinklet trekant AES kaldet en "levende" trekant i dette værk, da den er i stand til at generere visuelle billeder svarende til forskellige strukturelle elementer i naturen og tjene som en nøgle til at konstruere geometriske diagrammer af begyndelsen af udviklingen af nogle levende organismer.

Det andet eksempel er relateret til den første og tredje trekant i det gyldne snit. Fra de første to lige store trekanter af den gyldne proportion danner vi en rombe med indre vinkler på 72° og 108°. På samme måde kombinerer vi to lige store tredjetrekanter af den gyldne proportion til en rombe med indre vinkler på 36° og 144°. Hvis siderne af disse romber er lig med hinanden, kan de fylde et uendeligt plan uden hulrum eller overlapninger. Den tilsvarende algoritme til at fylde flyet blev udviklet i slutningen af 70'erne af det tyvende århundrede af teoretisk fysiker fra Oxford University R. Penrose. Desuden viste det sig, at det i den resulterende mosaik er umuligt at vælge en elementær celle med et helt antal rhombuses af hver type, hvis oversættelse ville gøre det muligt at opnå hele mosaikken. Men det mest bemærkelsesværdige var, at i den uendelige Penrose-mosaik er forholdet mellem antallet af "smalle" romber og antallet af "brede" nøjagtigt lig med værdien af det gyldne snit d = 0,61803...!

I dette eksempel er alle rødderne af det gyldne snit, udtrykt gennem vinkler, overraskende kombineret med et af tilfældene af ikke-triviel fyldning af et uendeligt plan med to elementære figurer - romber.

Afslutningsvis bemærker vi, at de forskellige eksempler givet ovenfor på sammenhængen mellem rødderne af ligningerne for den gyldne proportion og vinklerne for trekanter illustrerer, at den gyldne proportion er en mere rummelig opgave end tidligere forestillet. Hvis tidligere anvendelsesområdet for den gyldne proportion i sidste ende blev anset for at være forholdet mellem segmenter og forskellige sekvenser forbundet med de numeriske værdier af dens rødder (Fibonacci-tal), nu opdages det, at den gyldne proportion kan generere en række forskellige geometriske objekter, og ligningernes rødder har et eksplicit trigonometrisk udtryk.

Forfatterne er klar over, at det ovenfor udtrykte synspunkt vedrørende elegancen af de matematiske relationer forbundet med det gyldne snit afspejler personlige æstetiske oplevelser. I moderne filosofisk litteratur fortolkes begreberne æstetik og skønhed ret bredt og bruges snarere på et intuitivt plan. Disse begreber vedrører hovedsageligt kunst. Indholdet af videnskabelig kreativitet i æstetiske termer er praktisk talt ikke taget i betragtning i litteraturen. Som en første tilnærmelse til æstetiske parametre videnskabelig undersøgelse vi kan tilskrive deres komparative enkelhed, deres iboende symmetri og evnen til at generere visuelle billeder. Alle disse æstetiske parametre opfyldes af en opgave kaldet "den gyldne proportion". Generelt er problemerne med æstetik i videnskaben langt fra løst, selvom de er af stor interesse.

Det føles intuitivt, at det gyldne snit stadig skjuler sine hemmeligheder. Nogle af dem ligger muligvis på overfladen og venter på deres nye forskeres usædvanlige blik. Kendskab til egenskaberne ved det gyldne snit kan tjene som et godt grundlag for kreative mennesker, hvilket giver dem selvtillid og videnskab og i liv.

LITTERATUR

1. Shevelev I. Sh., Marutaev I. A., Shmelev I. P. Gyldne snit: Tre synspunkter om harmoniens natur.- M.: Stroyizdat, 1990. - 343 s.

2. Stakhov A. P. Gyldne snit koder.- M.: Radio og kommunikation, 1984. - 152 s.

3. Vasyutinsky N.A. Gyldent snit.- M.: Ung Garde, 1990. - 238 s.

4. Korobko V. I. Gyldne proportioner: Nogle filosofiske aspekter af harmoni.- M. - Orel: 2000. - 204 s.

5. Urmantsev Yu A. Gyldent snit// Nature, 1968, nr. 11.

6. Popkov V.V., Shipitsyn E.V. Gyldne forhold i Carnot-cyklussen// UFN, 2000, bind 170, nr.

7. Konstantinov I. Fantasier med et dodekaeder// Science and Life, 2001, nr. 2.

8. Shevelev I. Sh. Geometrisk harmoni// Videnskab og liv, 1965, nr. 8.

9. Gardner M. Fra Penrose flisebelægninger til stærke cifre. - M.: Mir, 1993.

En person skelner genstande omkring ham ved deres form. Interessen for et objekts form kan dikteres af vital nødvendighed, eller det kan være forårsaget af formens skønhed. Formen, hvis konstruktion er baseret på en kombination af symmetri og det gyldne snit, bidrager til den bedste visuelle opfattelse og fremkomsten af en følelse af skønhed og harmoni. Helheden består altid af dele, dele af forskellig størrelse står i et vist forhold til hinanden og til helheden. Princippet om det gyldne snit er den højeste manifestation af den strukturelle og funktionelle perfektion af helheden og dens dele i kunst, videnskab, teknologi og natur.

Gyldne forhold - harmonisk proportion

I matematik del(lat. proportio) kalder ligheden mellem to relationer:

-en : b = c : d.

Lige segment AB kan opdeles i to dele på følgende måder:

i to lige store dele - AB : A.C. = AB : B.C.;
i to ulige dele i nogen henseende (sådanne dele danner ikke proportioner);
altså hvornår AB : A.C. = A.C. : B.C..

Sidstnævnte er den gyldne opdeling eller opdeling af et segment i ekstreme og gennemsnitlige forhold.

Det gyldne snit er en sådan proportional opdeling af et segment i ulige dele, hvor hele segmentet er relateret til den større del, som den større del selv er relateret til den mindre; eller med andre ord, det mindre segment er til det større, som det større er for helheden:

-en : b = b : c
eller
c : b = b : -en.

Ris. 1. Geometrisk billede af det gyldne snit

Praktisk bekendtskab med det gyldne snit begynder med at dele et lige linjestykke i den gyldne proportion ved hjælp af et kompas og lineal.

Ris. 2.B.C. = 1/2 AB; CD = B.C.

Fra punkt B en vinkelret lig med halvdelen gendannes AB. Modtaget point C forbundet med en linje til et punkt EN. Et segment plottes på den resulterende linje B.C. slutter med en prik D. Linjestykke AD overført til direkte AB. Det resulterende punkt E opdeler et segment AB i det gyldne snit.

Segmenter af det gyldne snit udtrykkes som en uendelig irrationel fraktion A.E.= 0,618..., hvis AB tage som en VÆRE= 0,382... Til praktiske formål bruges der ofte omtrentlige værdier på 0,62 og 0,38. Hvis segmentet AB taget som 100 dele, så er den største del af segmentet lig med 62, og den mindre del er 38 dele.

Egenskaberne for det gyldne snit er beskrevet ved ligningen:

x 2 – x – 1 = 0.

Løsning til denne ligning:

Egenskaberne ved det gyldne snit har skabt en romantisk aura af mystik og næsten mystisk tilbedelse omkring dette nummer.

Andet gyldne snit

Det bulgarske magasin “Fatherland” (nr. 10, 1983) publicerede en artikel af Tsvetan Tsekov-Karandash “On the second golden section”, som følger af hovedafsnittet og giver endnu et forhold på 44:56.

Denne andel findes i arkitekturen og forekommer også, når man konstruerer kompositioner af billeder i et langstrakt vandret format.

Ris. 3.

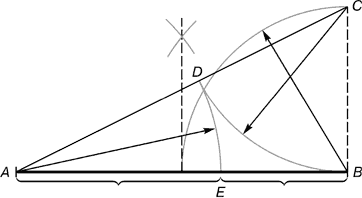
Opdelingen udføres som følger. Linjestykke AB opdelt efter det gyldne snit. Fra punkt C vinkelret gendannes CD. Radius AB der er en pointe D, som er forbundet med en linje til et punkt EN. Ret vinkel ACD er delt i to. Fra punkt C en linje tegnes indtil den skærer linjen AD. Prik E opdeler et segment AD i forhold til 56:44.

Ris. 4.

Figuren viser positionen af linjen i det andet gyldne snit. Den er placeret midt mellem det gyldne forholdslinje og rektanglets midterlinje.

Gyldne Trekant

For at finde segmenter af den gyldne del af den stigende og faldende række, kan du bruge pentagram.

Ris. 5. Konstruktion af en regulær femkant og pentagram

For at bygge et pentagram skal du bygge en almindelig femkant. Metoden til dens konstruktion blev udviklet af den tyske maler og grafiker Albrecht Durer (1471...1528). Lade O- midten af cirklen, EN– et punkt på en cirkel og E– midten af segmentet O.A.. Vinkelret på radius O.A., gendannet på punktet O, skærer cirklen i punktet D. Brug et kompas til at tegne et segment på diameteren C.E. = ED. Sidelængden af en regulær femkant indskrevet i en cirkel er DC. Læg segmenter ud på cirklen DC og vi får fem point for at tegne en regulær femkant. Vi forbinder hjørnerne af femkanten gennem hinanden med diagonaler og får et pentagram. Alle diagonaler i femkanten deler hinanden i segmenter forbundet med det gyldne snit.

Hver ende af den femkantede stjerne repræsenterer en gylden trekant. Dens sider danner en vinkel på 36° i spidsen, og bunden, lagt på siden, deler den i forholdet til det gyldne snit.

Ris. 6. Konstruktion af den gyldne trekant

Vi udfører en direkte AB. Fra punkt EN læg et segment på det tre gange O vilkårlig værdi gennem det resulterende punkt P tegne en vinkelret på linjen AB, på vinkelret på højre og venstre for punktet P læg segmenterne til side O. Modtaget point d Og d 1 forbindes med lige linjer til et punkt EN. Linjestykke dd sæt 1 på stregen Ad 1, får et point C. Hun delte linjen Ad 1 i forhold til det gyldne snit. Linjer Ad 1 og dd 1 bruges til at konstruere et "gyldent" rektangel.

Historien om det gyldne snit

Det er almindeligt accepteret, at begrebet den gyldne opdeling blev introduceret til videnskabelig brug af Pythagoras, en oldgræsk filosof og matematiker (VI århundrede f.Kr.). Der er en antagelse om, at Pythagoras lånte sin viden om den gyldne opdeling fra egypterne og babylonierne. Faktisk indikerer proportionerne af Cheops-pyramiden, templerne, basrelieffer, husholdningsartikler og dekorationer fra graven, at egyptiske håndværkere brugte forholdet mellem den gyldne division, når de skabte dem. Den franske arkitekt Le Corbusier fandt ud af, at i relieffet fra farao Seti I's tempel i Abydos og i relieffet, der afbilder farao Ramses, svarer figurernes proportioner til værdierne af den gyldne division. Arkitekten Khesira, afbildet på et relief af en træplade fra en grav opkaldt efter ham, holder i sine hænder måleinstrumenter, hvor proportionerne af den gyldne division er registreret.

Grækerne var dygtige geometre. De underviste endda deres børn i regne ved hjælp af geometriske figurer. Pythagoras kvadrat og diagonalen af denne firkant var grundlaget for konstruktionen af dynamiske rektangler.

Ris. 7. Dynamiske rektangler

Platon (427...347 f.Kr.) kendte også til den gyldne division. Hans dialog "Timaeus" er dedikeret til den pythagoras skoles matematiske og æstetiske synspunkter og i særdeleshed til spørgsmålene om den gyldne opdeling.

Facaden på det antikke græske tempel Parthenon har gyldne proportioner. Under dens udgravninger blev der opdaget kompasser, der blev brugt af arkitekter og billedhuggere fra den antikke verden. Det pompeianske kompas (museum i Napoli) indeholder også proportionerne af den gyldne inddeling.

Ris. 8.

I den antikke litteratur, der er kommet ned til os, blev den gyldne inddeling først nævnt i Euklids elementer. I Elementernes 2. bog er der givet en geometrisk konstruktion af den gyldne inddeling. Efter Euklid blev studiet af gylden division udført af Hypsicles (II århundrede f.Kr.), Pappus (III århundrede e.Kr.) og andre. middelalderlige Europa vi stiftede bekendtskab med den gyldne division igennem Arabiske oversættelser Euklids "Begyndelser". Oversætteren J. Campano fra Navarra (III århundrede) kom med kommentarer til oversættelsen. Hemmelighederne bag den gyldne division blev nidkært bevogtet og holdt i streng hemmelighed. De var kun kendt af indviede.

Under renæssancen steg interessen for den gyldne opdeling blandt videnskabsmænd og kunstnere på grund af dens brug i både geometri og kunst, især inden for arkitektur, Leonardo da Vinci, en kunstner og videnskabsmand, så, at italienske kunstnere havde meget empirisk erfaring, men kun lidt. viden . Han undfangede og begyndte at skrive en bog om geometri, men på det tidspunkt dukkede en bog af munken Luca Pacioli op, og Leonardo opgav sin idé. Ifølge samtidige og videnskabshistorikere var Luca Pacioli en rigtig lyskilde, Italiens største matematiker i perioden mellem Fibonacci og Galileo. Luca Pacioli var elev af maleren Piero della Franceschi, som skrev to bøger, hvoraf den ene havde titlen On Perspective in Painting. Han betragtes som skaberen af beskrivende geometri.

Luca Pacioli forstod perfekt videnskabens betydning for kunsten. I 1496 kom han på invitation af hertug Moreau til Milano, hvor han holdt forelæsninger om matematik. Leonardo da Vinci arbejdede også i Milano ved Moro-hoffet på det tidspunkt. I 1509 blev Luca Paciolis bog "The Divine Proportion" udgivet i Venedig med glimrende udførte illustrationer, hvorfor det menes, at de er lavet af Leonardo da Vinci. Bogen var en begejstret salme til det gyldne snit. Blandt de mange fordele ved den gyldne proportion undlod munken Luca Pacioli ikke at navngive dens "guddommelige essens" som et udtryk for den guddommelige treenighed - Gud Faderen, Gud Sønnen og Gud Helligånden (det blev antydet, at den lille segment er personificeringen af Gud Sønnen, det større segment er Gud Fader, og hele segmentet - Gud Helligånden).

E-bøger:

Mario Livio.

18/04/2011 A. F. Afanasyev Opdateret 16/06/12

Dimensioner og proportioner er en af hovedopgaverne i søgningen efter et kunstnerisk billede af ethvert plastisk kunstværk. Det er klart, at spørgsmålet om størrelse afgøres under hensyntagen til rummet, hvor det vil blive placeret, og genstandene omkring det.

Når vi taler om proportioner (forhold mellem dimensionelle værdier), tager vi hensyn til dem i formatet af et fladt billede (maleri, marquetry), i forholdet mellem overordnede dimensioner (længde, højde, bredde) af en volumetrisk genstand, i forholdet mellem to objekter af et ensemble forskellige i højde eller længde, i forholdet størrelserne af to klart synlige dele af samme genstand osv.

I klassikerne inden for kunst i mange århundreder er en teknik til at konstruere proportioner blevet sporet, kaldet det gyldne snit eller det gyldne tal (dette udtryk blev introduceret af Leonardo da Vinci). Princippet om det gyldne snit, eller dynamisk symmetri, er, at "forholdet mellem to dele af en enkelt helhed er lig med forholdet mellem dens største del og helheden" (eller følgelig helheden til den større del). Matematisk er dette

tallet er udtrykt som - 1 ± 2?5 - hvilket giver 1,6180339... eller 0,6180339... I kunsten tages 1,62 som det gyldne tal, dvs. et tilnærmet udtryk for forholdet mellem en større værdi i forhold til dens mindre værdi.
Fra omtrentlig til mere nøjagtig kan denne sammenhæng udtrykkes: osv., hvor: 5+3=8, 8+5=13 osv. Eller: 2,2:3,3:5,5:8 ,8 osv. ., hvor 2,2+3,3-5,5 osv.

Grafisk kan det gyldne snit udtrykkes ved forholdet mellem segmenter opnået ved forskellige konstruktioner. Mere bekvemt, efter vores mening, er konstruktionen vist i fig. 169: hvis du lægger dens korte side til diagonalen af en halv firkant, får du en værdi i forholdet mellem det gyldne tal og dets lange side.

Ris. 169. Geometrisk konstruktion af et rektangel i det gyldne snit 1,62: 1. Gyldent tal 1,62 i forhold til segmenter (a og b)

Ris. 170. Grafisk konstruktion af funktionen gyldne snit 1,12:1

Andel af to gyldne snit

skaber en visuel følelse af harmoni og balance. Der er et andet harmonisk forhold mellem to tilstødende mængder, udtrykt ved tallet 1,12. Det er en funktion af det gyldne tal: hvis du tager forskellen mellem to værdier af det gyldne snit, deler det også i det gyldne snit og lægger hver brøkdel til den mindre værdi af det oprindelige gyldne snit, får du et forhold på 1,12 (fig. 170). I denne relation er for eksempel det midterste element (hylden) tegnet i bogstaverne H, R, Z osv. i nogle skrifttyper er proportionerne mellem højde og bredde taget for brede bogstaver, denne relation findes også i naturen.

Det gyldne tal observeres i proportionerne af en harmonisk udviklet person (fig. 171): hovedets længde deler afstanden fra taljen til kronen i det gyldne snit; knæskallen deler også afstanden fra taljen til fodsålen; spidsen af langfingeren på en udstrakt hånd deler hele højden af en person i den gyldne proportion; Forholdet mellem fingrenes phalanges er også et gyldent tal. Det samme fænomen observeres i andre strukturer i naturen: i bløddyrs spiraler, i blomsterkroner osv.

Ris. 172. Gyldne proportioner af et udskåret geraniumblad (pelargonium). Konstruktion: 1) Ved hjælp af en skalagraf (se fig. 171) bygger vi? ABC,	Ris. 173. Fembladede og trebladede drueblade. Forholdet mellem længde og bredde er 1,12. Det gyldne snit er udtrykt

I fig. 172 og 173 viser konstruktionen af et mønster af et geranium (pelargonium) blad og et drueblad i proportionerne af gyldne tal 1,62 og 1,12. I et geraniumblad er konstruktionsgrundlaget to trekanter: ABC og CEF, hvor forholdet mellem højden og bunden af hver af dem er udtrykt med tallene 0,62 og 1,62, og afstandene mellem de tre par af de fjerneste punkter på bladet er ens: AB=CE=SF. Konstruktionen er angivet på tegningen. Designet af et sådant blad er typisk for geranier, som har lignende udskårne blade.

Det generaliserede platanblad (Fig. 173) har samme proportioner som druebladet, i forholdet 1,12, men den største andel af druebladet er dets længde, og platanbladets bredde er dets. Platanbladene har tre proportionale størrelser i forholdet 1,62. En sådan korrespondance i arkitektur kaldes en triade (for fire proportioner - tetrad og videre: pectad, hexode).

I fig. 174 viser en metode til at konstruere et ahornblad i proportionerne med det gyldne snit. Med et forhold mellem bredde og længde på 1,12 har den flere proportioner med tallet 1,62. Konstruktionen er baseret på to trapezoider, hvor forholdet mellem bundens højde og længde er udtrykt med et gyldent tal. Konstruktionen er vist på tegningen, og der er også givet muligheder for formen på et ahornblad.

I kunstværker anvender en kunstner eller billedhugger, bevidst eller ubevidst, som stoler på sit trænede øje, ofte størrelsesforholdet i det gyldne snit. Mens han arbejdede på en kopi af Kristi hoved (ifølge Michelangelo), bemærkede forfatteren af denne bog, at tilstødende krøller i hårstrå i deres størrelse afspejler forholdet mellem det gyldne snit og i deres form - den arkimedeiske spiral , det involvente. Læseren kan selv se, at i en række malerier af klassiske kunstnere er den centrale figur placeret fra siderne af formatet i afstande, der danner andelen af det gyldne snit (f.eks. placeringen af hovedet både lodret og vandret i V . Borovikovskys portræt af M. I. Lopukhina langs hovedets lodrette midte i portrættet af A. S. Pushkin af O. Kiprensky og andre). Det samme kan nogle gange ses med placeringen af horisontlinjen (F. Vasiliev: "Wet Meadow", I. Levitan: "March", "Aftenklokker").

Selvfølgelig er denne regel ikke altid en løsning på problemet med komposition, og den bør ikke erstatte intuitionen af rytme og proportioner i kunstnerens arbejde. Det er for eksempel kendt, at nogle kunstnere brugte forholdet mellem "musikalske numre" til deres kompositioner: tredjedele, fjerdedele, femtedele (2:3, 3:4 osv.). Kunsthistorikere bemærker, ikke uden grund, at designet af ethvert klassisk arkitektonisk monument eller skulptur, hvis det ønskes, kan justeres til ethvert talforhold. Vores opgave i dette tilfælde, og især opgaven for en begyndende kunstner eller træskærer, er at lære at bygge en bevidst komposition af sit værk, ikke efter tilfældige forhold, men efter harmoniske proportioner, bevist ved praksis. Disse harmoniske proportioner skal kunne identificeres og understreges af produktets design og form.

Som et eksempel på at finde en harmonisk proportion kan du overveje at bestemme størrelsen af rammen til arbejdet vist i fig. 175. Formatet på billedet, der er placeret i det, er indstillet i forholdet til det gyldne snit. Udvendige dimensioner rammer med samme bredde af sine sider vil ikke give den gyldne proportion. Derfor antages forholdet mellem dets længde og bredde (ЗЗ0X220) at være lidt mindre end det gyldne tal, dvs. lig med 1,5, og bredden af de tværgående led øges tilsvarende sammenlignet med sidesiderne. Dette gjorde det muligt at nå frem til rammens dimensioner i lyset (til maleriet), hvilket gav proportionerne af det gyldne snit. Forholdet mellem bredden af rammens nederste led og bredden af dens øvre led justeres til et andet gyldent tal, dvs. 1,12. Også forholdet mellem bredden af det nederste led og bredden af sideleddet (94:63) er tæt på 1,5 (i figuren - muligheden til venstre).

Lad os nu lave et eksperiment: vi øger den lange side af rammen til 366 mm på grund af bredden af det nederste led (det vil være 130 mm) (på billedet - muligheden til højre), hvilket ikke kun bringer forholdet tættere på, men også på guldet
nummer 1,62 i stedet for 1,12. Resultatet er en ny sammensætning, der kan bruges i et andet produkt, men til stellet er der et ønske om at gøre det kortere. Dæk dens nederste del med en lineal så meget, at øjet "accepterer" den resulterende andel, og vi får dens længde på 330 mm, dvs. vi nærmer os den originale version.

Altså at analysere forskellige muligheder(der kan være andre end de to diskuterede), standser mesteren ved den eneste mulige løsning fra sit synspunkt.

Det er bedst at anvende princippet om det gyldne forhold på jagt efter den ønskede sammensætning ved hjælp af en simpel enhed, hvis grundlæggende designdiagram er vist i fig. 176. To linealer af denne enhed kan, roterende omkring hængsel B, danne en vilkårlig vinkel. Hvis vi for en vinkelløsning deler afstanden AC i det gyldne snit med et punkt K og monterer yderligere to linealer: KM\\BC og KE\\AB med hængsler i punkterne K, E og M, så for enhver løsning AC denne afstand vil blive divideret med punktet K i forhold til det gyldne snit.

Victor Lavrus

Gyldne forhold - harmonisk proportion

I matematik del(lat. proportio) kalder ligheden mellem to relationer: -en : b = c : d.

Lige segment AB kan opdeles i to dele på følgende måder:

i to lige store dele - AB : AC = AB : Sol;

i to ulige dele i nogen henseende (sådanne dele danner ikke proportioner);

altså hvornår AB : AC = AC : Sol.

Sidstnævnte er den gyldne opdeling eller opdeling af et segment i ekstreme og gennemsnitlige forhold.

-en : b = b : c eller Med : b = b : EN.

Ris. 1. Geometrisk billede af det gyldne snit

Praktisk bekendtskab med det gyldne snit begynder med at dele et lige linjestykke i den gyldne proportion ved hjælp af et kompas og lineal.

Ris. 2. Opdeling af et lige linjestykke ved hjælp af det gyldne snit. B.C. = 1/2 AB; CD = B.C.

Fra punkt I en vinkelret lig med halvdelen gendannes AB. Modtaget point MED forbundet med en linje til et punkt EN. Et segment plottes på den resulterende linje Sol slutter med en prik D. Linjestykke AD overført til direkte AB. Det resulterende punkt E opdeler et segment AB i det gyldne snit.

Egenskaberne for det gyldne snit er beskrevet ved ligningen:

x 2 - x - 1 = 0.

Løsning til denne ligning:

Egenskaberne ved det gyldne snit har skabt en romantisk aura af mystik og næsten mystisk tilbedelse omkring dette nummer.

Andet gyldne snit

Det bulgarske magasin "Fatherland" (nr. 10, 1983) publicerede en artikel af Tsvetan Tsekov-Karandash "Om det andet gyldne snit", som følger af hovedafsnittet og giver endnu et forhold på 44:56.

Denne andel findes i arkitekturen og forekommer også, når man konstruerer kompositioner af billeder i et langstrakt vandret format.

Ris. 3. Konstruktion af det andet gyldne snit

Opdelingen udføres som følger (se fig. 3). Linjestykke AB opdelt efter det gyldne snit. Fra punkt MED vinkelret gendannes CD. Radius AB der er en pointe D, som er forbundet med en linje til et punkt EN. Ret vinkel ACD er delt i to. Fra punkt MED en linje tegnes indtil den skærer linjen AD. Prik E opdeler et segment AD i forhold til 56:44.

Ris. 4. Opdeling af et rektangel med linjen i det andet gyldne snit

I fig. Figur 4 viser positionen af linjen i det andet gyldne snit. Den er placeret midt mellem det gyldne forholdslinje og rektanglets midterlinje.

Gyldne Trekant

For at finde segmenter af den gyldne del af den stigende og faldende række, kan du bruge pentagram.

Ris. 5. Konstruktion af en regulær femkant og pentagram

For at bygge et pentagram skal du bygge en almindelig femkant. Metoden til dens konstruktion blev udviklet af den tyske maler og grafiker Albrecht Durer (1471...1528). Lade O- midten af cirklen, EN- et punkt på en cirkel og E- midten af segmentet OA. Vinkelret på radius OA, gendannet på punktet OM, skærer cirklen i punktet D. Brug et kompas til at tegne et segment på diameteren C.E. = ED. Sidelængden af en regulær femkant indskrevet i en cirkel er DC. Læg segmenter ud på cirklen DC og vi får fem point for at tegne en regulær femkant. Vi forbinder hjørnerne af femkanten gennem hinanden med diagonaler og får et pentagram. Alle diagonaler i femkanten deler hinanden i segmenter forbundet med det gyldne snit.

Hver ende af den femkantede stjerne repræsenterer en gylden trekant. Dens sider danner en vinkel på 36° i spidsen, og bunden, lagt på siden, deler den i forholdet til det gyldne snit.

Ris. 6. Konstruktion af den gyldne trekant

Vi udfører en direkte AB. Fra punkt EN læg et segment på det tre gange OM vilkårlig værdi gennem det resulterende punkt R tegne en vinkelret på linjen AB, på vinkelret på højre og venstre for punktet R læg segmenterne til side OM. Modtaget point d Og d 1 forbindes med lige linjer til et punkt EN. Linjestykke dd sæt 1 på stregen Ad 1, får et point MED. Hun delte linjen Ad 1 i forhold til det gyldne snit. Linjer Ad 1 og dd 1 bruges til at konstruere et "gyldent" rektangel.

Historien om det gyldne snit

Det er almindeligt accepteret, at begrebet den gyldne opdeling blev introduceret til videnskabelig brug af Pythagoras, en oldgræsk filosof og matematiker (VI århundrede f.Kr.). Der er en antagelse om, at Pythagoras lånte sin viden om den gyldne opdeling fra egypterne og babylonierne. Faktisk indikerer proportionerne af Cheops-pyramiden, templerne, basrelieffer, husholdningsartikler og smykker fra Tutankhamons grav, at egyptiske håndværkere brugte forholdet mellem den gyldne division, da de skabte dem. Den franske arkitekt Le Corbusier fandt ud af, at i relieffet fra farao Seti I's tempel i Abydos og i relieffet, der afbilder farao Ramses, svarer figurernes proportioner til værdierne af den gyldne division. Arkitekten Khesira, afbildet på et relief af en træplade fra en grav opkaldt efter ham, holder i sine hænder måleinstrumenter, hvor proportionerne af den gyldne division er registreret.

Ris. 7. Dynamiske rektangler

Platon (427...347 f.Kr.) kendte også til den gyldne division. Hans dialog "Timaeus" er viet til de matematiske og æstetiske synspunkter i den pythagoræiske skole og i særdeleshed til spørgsmålene om den gyldne opdeling.

Ris. 8. Antik kompas med gyldne snit

I den antikke litteratur, der er kommet ned til os, blev den gyldne inddeling først nævnt i Euklids elementer. I den 2. bog af "Principlene" er den geometriske konstruktion af den gyldne inddeling givet middelalderens Europa, med den gyldne opdeling Vi mødtes gennem arabiske oversættelser af Euklids elementer. Oversætteren J. Campano fra Navarra (III århundrede) kom med kommentarer til oversættelsen. Hemmelighederne bag den gyldne division blev nidkært bevogtet og holdt i streng hemmelighed. De var kun kendt af indviede.

Under renæssancen steg interessen for den gyldne opdeling blandt videnskabsmænd og kunstnere på grund af dens brug i både geometri og kunst, især inden for arkitektur, Leonardo da Vinci, en kunstner og videnskabsmand, så, at italienske kunstnere havde meget empirisk erfaring, men kun lidt. viden . Han undfangede og begyndte at skrive en bog om geometri, men på det tidspunkt dukkede en bog af munken Luca Pacioli op, og Leonardo opgav sin idé. Ifølge samtidige og videnskabshistorikere var Luca Pacioli en rigtig lyskilde, Italiens største matematiker i perioden mellem Fibonacci og Galileo. Luca Pacioli var en elev af kunstneren Piero della Franceschi, som skrev to bøger, hvoraf den ene hed "On Perspective in Painting." Han betragtes som skaberen af beskrivende geometri.

Luca Pacioli forstod perfekt videnskabens betydning for kunsten. I 1496 kom han på invitation af hertugen af Moreau til Milano, hvor han holdt foredrag om matematik. Leonardo da Vinci arbejdede også i Milano ved Moro-hoffet på det tidspunkt. I 1509 blev Luca Paciolis bog "The Divine Proportion" udgivet i Venedig med glimrende udførte illustrationer, hvorfor det menes, at de er lavet af Leonardo da Vinci. Bogen var en begejstret salme til det gyldne snit. Blandt de mange fordele ved den gyldne proportion undlod munken Luca Pacioli ikke at nævne dens "guddommelige essens" som et udtryk for den guddommelige treenighed - Gud sønnen, Gud faderen og Gud den hellige ånd (det blev antydet, at den lille segmentet er personificeringen af Gud sønnen, det større segment - Gud faderen, og hele segmentet - Helligåndens Gud).

Leonardo da Vinci var også meget opmærksom på studiet af den gyldne division. Han lavede sektioner af et stereometrisk legeme dannet af regulære femkanter, og hver gang fik han rektangler med aspektforhold i den gyldne division. Det var derfor, han gav denne afdeling navnet gyldne snit. Så det forbliver stadig som det mest populære.

Samtidig arbejdede Albrecht Dürer i det nordlige Europa i Tyskland med de samme problemer. Han skitserer indledningen til den første version af afhandlingen om proportioner. Dürer skriver. ”Det er nødvendigt, at en, der ved, hvordan man gør noget, skal lære det til andre, der har brug for det. Det er, hvad jeg satte mig for at gøre."

At dømme efter et af Dürers breve mødtes han med Luca Pacioli, mens han var i Italien. Albrecht Durer udvikler i detaljer teorien om proportioner af den menneskelige krop. Dürer tildelte det gyldne snit en vigtig plads i sit system af relationer. En persons højde er opdelt i gyldne proportioner af bæltets linje, såvel som af en linje trukket gennem spidserne af langfingrene på de sænkede hænder, den nederste del af ansigtet ved munden osv. Dürers proportionale kompas er velkendt.

Stor astronom fra det 16. århundrede. Johannes Kepler kaldte det gyldne snit for en af geometriens skatte. Han var den første til at henlede opmærksomheden på betydningen af den gyldne proportion for botanik (plantevækst og deres struktur).

Kepler kaldte den gyldne proportion selv-fortsættende "Den er struktureret på en sådan måde," skrev han, "at de to laveste led i denne uendelige andel lægger op til det tredje led, og alle to sidste led, hvis de lægges sammen. , giv det næste led, og det samme forhold bibeholdes indtil det uendelige."

Konstruktionen af en række segmenter af den gyldne proportion kan udføres både i retning af stigning (stigende serie) og i retning af fald (faldende serie).

Hvis du er på en lige linje af vilkårlig længde, skal du lægge segmentet til side m, sæt segmentet ved siden af M. Baseret på disse to segmenter bygger vi en skala af segmenter af den gyldne del af de stigende og faldende serier

Ris. 9. Konstruktion af en skala af gyldne proportionssegmenter

I de efterfølgende århundreder blev reglen om den gyldne proportion til en akademisk kanon, og da kampen mod den akademiske rutine med tiden begyndte i kunsten, "smed de i kampens hede barnet ud med badevandet." Det gyldne snit blev "opdaget" igen i midten af 1800-tallet. I 1855 udgav den tyske forsker i det gyldne snit, professor Zeising, sit værk "Aesthetic Studies". Det, der skete med Zeising, var præcis, hvad der uundgåeligt skulle ske for en forsker, der betragter et fænomen som sådan, uden sammenhæng med andre fænomener. Han absolutiserede andelen af det gyldne snit og erklærede det universelt for alle natur- og kunstfænomener. Zeising havde adskillige tilhængere, men der var også modstandere, der erklærede hans doktrin om proportioner for at være "matematisk æstetik."

Ris. 10. Gyldne proportioner i dele af den menneskelige krop

Zeising gjorde et fantastisk stykke arbejde. Han målte omkring to tusinde menneskekroppe og kom til den konklusion, at det gyldne snit udtrykker den gennemsnitlige statistiske lov. Opdelingen af kroppen med navlespidsen er den vigtigste indikator for det gyldne snit. Proportioner mandlig krop svinge inden for det gennemsnitlige forhold på 13: 8 = 1,625 og er noget tættere på det gyldne snit end proportionerne af kvindekroppen, i forhold til hvilke den gennemsnitlige værdi af andelen er udtrykt i forholdet 8: 5 = 1,6. Hos en nyfødt er andelen 1:1, i en alder af 13 er den 1,6, og i en alder af 21 er den lig med en mands. Proportionerne af det gyldne snit viser sig også i forhold til andre dele af kroppen - længden af skulder, underarm og hånd, hånd og fingre mv.

Ris. elleve. Gyldne proportioner i den menneskelige figur

Zeising testede gyldigheden af sin teori på græske statuer. Han udviklede proportionerne af Apollo Belvedere i de mest detaljerede. Græske vaser og arkitektoniske strukturer blev undersøgt forskellige epoker, planter, dyr, fugleæg, musikalske toner, poetiske metre. Zeising gav en definition af det gyldne snit og viste, hvordan det udtrykkes i lige linjestykker og i tal. Da tallene, der udtrykte længderne af segmenterne, blev opnået, så Zeising, at de udgjorde en Fibonacci-serie, som kunne fortsættes i det uendelige i den ene eller den anden retning. Hans næste bog fik titlen "Den gyldne division som den grundlæggende morfologiske lov i naturen og kunsten." I 1876 blev en lille bog, nærmest en brochure, udgivet i Rusland, der skitserede Zeisings arbejde. Forfatteren søgte tilflugt under initialerne Yu.F.V. Denne udgave omtaler ikke et eneste malerværk.

I slutningen af XIX- begyndelsen af det 20. århundrede Der dukkede mange rent formalistiske teorier op om brugen af det gyldne snit i kunstværker og arkitektur. Med udviklingen af design og teknisk æstetik udvidede loven om det gyldne snit til design af biler, møbler mv.

Fibonacci-serien

Navnet på den italienske matematikermunk Leonardo af Pisa, bedre kendt som Fibonacci (søn af Bonacci), er indirekte forbundet med historien om det gyldne snit. Han rejste meget i østen, introducerede Europa til indiske (arabiske) tal. I 1202 udkom hans matematiske værk "The Book of the Abacus" (tællebræt), som samlede alle de problemer, der var kendt på det tidspunkt. Et af problemerne lød: "Hvor mange par kaniner bliver der født fra et par på et år." Efter at have reflekteret over dette emne byggede Fibonacci følgende serie af tal:

En række tal 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 osv. kendt som Fibonacci-serien. Det særlige ved talrækken er, at hvert af dets medlemmer, startende fra den tredje, lig med summen to foregående 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 osv., og forholdet mellem tilstødende tal i rækken nærmer sig forholdet mellem den gyldne division. Så 21: 34 = 0,617 og 34: 55 = 0,618. Dette forhold er angivet med symbolet F. Kun dette forhold - 0,618: 0,382 - giver en kontinuerlig opdeling af et lige linjestykke i den gyldne proportion, hvilket øger eller formindsker det til det uendelige, når det mindre segment er relateret til det større, som det større er til helheden.

Fibonacci beskæftigede sig også med handelens praktiske behov: Hvad er det mindste antal vægte, der kan bruges til at veje et produkt? Fibonacci beviser, at det optimale vægtsystem er: 1, 2, 4, 8, 16...

Generaliseret gyldne snit

Fibonacci-serien kunne kun være forblevet en matematisk hændelse, hvis ikke for det faktum, at alle forskere af den gyldne division i plante- og dyreverdenen, for ikke at nævne kunst, uvægerligt kom til denne serie som et aritmetisk udtryk for loven om det gyldne division.

Forskere fortsatte aktivt med at udvikle teorien om Fibonacci-tal og det gyldne snit. Yu Matiyasevich løser Hilberts 10. problem ved hjælp af Fibonacci-tal. Elegante metoder dukker op til at løse en række kybernetiske problemer (søgeteori, spil, programmering) ved hjælp af Fibonacci-tal og det gyldne snit. I USA oprettes selv Mathematical Fibonacci Association, som siden 1963 har udgivet et specialtidsskrift.

En af resultaterne på dette felt er opdagelsen af generaliserede Fibonacci-tal og generaliserede gyldne snit.

Fibonacci-serien (1, 1, 2, 3, 5, 8) og den "binære" serie af vægte opdaget af ham 1, 2, 4, 8, 16... ved første øjekast er helt anderledes. Men algoritmerne til deres konstruktion ligner hinanden meget: i det første tilfælde er hvert tal summen af det foregående tal med sig selv 2 = 1 + 1; 4 = 2 + 2..., i det andet er det summen af de to foregående tal 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Er det muligt at finde en generel matematisk beregning formel, hvorfra vi får og " binære serier og Fibonacci serier? Eller måske vil denne formel give os nyt nummersæt, besidder nogle nye unikke egenskaber?

Faktisk, lad os indstille den numeriske parameter S, som kan have en hvilken som helst værdi: 0, 1, 2, 3, 4, 5... Overvej en talserie, S+ 1, hvoraf de første led er enheder, og hver af de efterfølgende er lig med summen af to led af den foregående og adskilt fra den foregående med S trin. Hvis n Vi betegner det te led i denne række ved φ S ( n), så får vi den generelle formel φ S ( n) = φ S ( n- 1) + φ S ( n - S - 1).

Det er indlysende, at hvornår S= 0 fra denne formel får vi en "binær" serie, med S= 1 - Fibonacci-serien, med S= 2, 3, 4. nye talrækker, som kaldes S-Fibonacci-tal.

Generelt gyldent S-Proportion er den positive rod af den gyldne ligning S-sektioner x S+1 - x S - 1 = 0.

Det er nemt at vise, hvornår S= 0, segmentet er delt i to, og hvornår S= 1 - det velkendte klassiske gyldne snit.

Relationer mellem naboer S- Fibonacci-tal falder sammen med absolut matematisk nøjagtighed i grænsen med guld S-proportioner! Matematikere i sådanne tilfælde siger, at guld S-sektioner er numeriske invarianter S-Fibonacci-tal.

Fakta, der bekræfter eksistensen af guld S-sektioner i naturen, citerer den hviderussiske videnskabsmand E.M. Soroko i bogen "Structural Harmony of Systems" (Minsk, "Science and Technology", 1984). Det viser sig f.eks., at velundersøgte binære legeringer kun har særlige, udtalte funktionelle egenskaber (termisk stabile, hårde, slidbestandige, oxidationsbestandige osv.) specifik vægtfylde de originale komponenter er forbundet med hinanden af en af guldet S-proportioner. Dette gjorde det muligt for forfatteren at fremsætte hypotesen om, at guld S-sektioner er numeriske invarianter af selvorganiserende systemer. Når først bekræftet eksperimentelt, kan denne hypotese være af fundamental betydning for udviklingen af synergetik - et nyt videnskabsområde, der studerer processer i selvorganiserende systemer.

Brug af guldkoder S-Proportioner kan udtrykkes ved et hvilket som helst reelt tal som summen af guldmagter S-proportioner med heltalskoefficienter.

Den grundlæggende forskel mellem denne metode til indkodning af tal er, at de nye koders baser er gyldne S-proportioner, med S> 0 viser sig at være irrationelle tal. Således ser nye talsystemer med irrationelle baser ud til at sætte det historisk etablerede hierarki af relationer mellem rationelle og irrationelle tal "fra top til fod." Faktum er, at naturlige tal først blev "opdaget"; så er deres forhold rationelle tal. Og først senere - efter opdagelsen af inkommensurable segmenter af pythagoræerne - blev irrationelle tal født. For eksempel i decimal-, quinær-, binære og andre klassiske positionstalssystemer blev naturlige tal valgt som en slags grundlæggende princip - 10, 5, 2 - hvoraf visse regler alle andre naturlige tal, såvel som rationelle og irrationelle tal, blev konstrueret.

En slags alternativ til eksisterende notationsmetoder er et nyt, irrationelt system, som et grundlæggende princip, hvis begyndelse er et irrationelt tal (som, husker jeg, er roden til ligningen med det gyldne snit); andre reelle tal er allerede udtrykt gennem det.

I sådan et talsystem kan evt naturligt tal altid repræsenteret som endeligt - og ikke uendeligt, som tidligere antaget! - summen af graderne af noget af guldet S-proportioner. Dette er en af grundene til, at "irrationel" aritmetik, der besidder fantastisk matematisk enkelhed og elegance, synes at have absorberet bedste kvaliteter klassisk binær og Fibonacci aritmetik.

Principper for dannelse i naturen

Alt, der antog en eller anden form, blev dannet, voksede, stræbte efter at tage plads i rummet og bevare sig selv. Dette ønske realiseres hovedsageligt i to muligheder - at vokse opad eller sprede sig over jordens overflade og sno sig i en spiral.

Skallen er snoet i en spiral. Folder du den ud, får du en længde lidt kortere end slangens længde. En lille ti-centimeter skal har en spiral på 35 cm. Spiraler er meget almindelige i naturen. Ideen om det gyldne snit vil være ufuldstændig uden at tale om spiralen.

Ris. 12. Archimedes spiral

Formen på den spiralkrøllede skal tiltrak Archimedes opmærksomhed. Han studerede det og fandt på en ligning for spiralen. Spiralen tegnet i henhold til denne ligning kaldes ved hans navn. Stigningen i hendes skridt er altid ensartet. I øjeblikket er Archimedes-spiralen meget brugt i teknologi.

Goethe fremhævede også naturens tendens til spiralitet. Det spiralformede og spiralformede arrangement af blade på trægrene blev bemærket for længe siden. Spiralen blev set i arrangementet af solsikkefrø, kogler, ananas, kaktusser osv. Botanikeres og matematikeres fælles arbejde har kastet lys over disse fantastiske fænomener natur. Det viste sig, at Fibonacci-serien manifesterer sig i arrangementet af blade på en gren (phylotaxis), solsikkefrø og fyrrekogler, og derfor manifesterer loven om det gyldne snit sig. Edderkoppen væver sit spind i et spiralmønster. En orkan snurrer som en spiral. Skræmt flok rensdyr spiraler væk. DNA-molekylet er snoet i en dobbelt helix. Goethe kaldte spiralen "livets kurve".

Blandt vejkantens urter vokser en umærkelig plante - cikorie. Lad os se nærmere på det. Et skud er dannet fra hovedstammen. Det første blad var placeret lige der.

Ris. 13. Cikorie

Skuddet laver et kraftigt udkast ud i rummet, stopper, udløser et blad, men denne gang er det kortere end det første, laver igen et udkast ud i rummet, men med mindre kraft, udløser et blad af endnu mindre størrelse og skydes ud igen . Hvis den første emission tages som 100 enheder, så er den anden lig med 62 enheder, den tredje - 38, den fjerde - 24 osv. Længden af kronbladene er også underlagt den gyldne proportion. I at vokse og erobre plads, opretholdt planten visse proportioner. Impulserne fra dens vækst faldt gradvist i forhold til det gyldne snit.

Ris. 14. Viviparøs firben

Ved første øjekast har firbenet proportioner, der er behagelige for vores øjne - længden af dens hale er relateret til længden af resten af kroppen som 62 til 38.

I både plante- og dyreverdenen bryder naturens dannelsestendens vedvarende igennem - symmetri om vækst- og bevægelsesretning. Her vises det gyldne snit i proportionerne af dele vinkelret på vækstretningen.

Naturen har udført opdeling i symmetriske dele og gyldne proportioner. Delene afslører en gentagelse af helhedens struktur.

Ris. 15. fugleæg

Den store Goethe, en digter, naturforsker og kunstner (han tegnede og malede i akvareller), drømte om at skabe en samlet doktrin om form, dannelse og transformation af organiske legemer. Det var ham, der introducerede begrebet morfologi i videnskabelig brug.

Pierre Curie formulerede i begyndelsen af dette århundrede en række dybe ideer om symmetri. Han argumenterede for, at man ikke kan overveje symmetrien af nogen krop uden at tage hensyn til miljøets symmetri.

Mønstrene af "gyldne" symmetri manifesteres i energiovergange elementære partikler, i strukturen af nogle kemiske forbindelser, i planetariske og kosmiske systemer, i levende organismers genstrukturer. Disse mønstre, som angivet ovenfor, eksisterer i strukturen af individuelle menneskelige organer og kroppen som helhed og manifesterer sig også i hjernens biorytmer og funktion og visuel perception.

Gyldne forhold og symmetri

Det gyldne snit kan ikke betragtes alene, separat, uden forbindelse med symmetri. Den store russiske krystallograf G.V. Wulf (1863...1925) anså det gyldne snit for at være et af symmetriens manifestationer.

Den gyldne opdeling er ikke en manifestation af asymmetri, noget modsat symmetri Ifølge moderne ideer er den gyldne opdeling asymmetrisk symmetri. Videnskaben om symmetri omfatter sådanne begreber som statisk Og dynamisk symmetri. Statisk symmetri kendetegner fred og balance, mens dynamisk symmetri kendetegner bevægelse og vækst. I naturen er statisk symmetri således repræsenteret af strukturen af krystaller, og i kunsten kendetegner den fred, balance og ubevægelighed. Dynamisk symmetri udtrykker aktivitet, karakteriserer bevægelse, udvikling, rytme, det er bevis på liv. Statisk symmetri er karakteriseret ved lige store segmenter og lige værdier. Dynamisk symmetri er karakteriseret ved en stigning i segmenter eller deres fald, og det udtrykkes i værdierne af det gyldne snit i en stigende eller faldende serie.

Gyldne proportioner i litteraturen. Poesi og det gyldne snit

Meget i strukturen af poetiske værker gør, at denne kunstform ligner musik. En klar rytme, en naturlig vekslen mellem understregede og ubetonede stavelser, en ordnet meter af digte og deres følelsesmæssige rigdom gør poesi søster musikalske værker. Hvert vers har sin egen musikalske form – sin egen rytme og melodi. Man kan forvente, at nogle træk ved musikværker, lovene for musikalsk harmoni og følgelig den gyldne proportion vil optræde i digtets struktur.

Lad os starte med digtets størrelse, det vil sige antallet af linjer i det. Det ser ud til, at denne parameter i digtet kan ændre sig vilkårligt. Det viste sig dog, at det ikke var tilfældet. For eksempel N. Vasyutinskys analyse af digte af A.S. Pushkin fra dette synspunkt viste, at størrelserne af digte er fordelt meget ujævnt; det viste sig, at Pushkin klart foretrækker størrelserne 5, 8, 13, 21 og 34 linjer (Fibonacci-tal).

Mange forskere har bemærket, at digte ligner musikstykker; de har også kulminerende punkter, der deler digtet i forhold til det gyldne snit. Overvej for eksempel digtet af A.S. Pushkins "Skomager":

En skomager så engang ud efter maleriet
Og han påpegede fejlen i skoene;
Kunstneren tog straks sin pensel og rettede sig selv,
Så med sine arme akimbo fortsatte skomageren:
"Jeg synes, ansigtet er lidt skævt...
Er disse bryster ikke for nøgne?
Her afbrød Apelles utålmodigt:
"Døm, min ven, ikke højere end støvlen!"

jeg har en ven hold øje:
Jeg ved ikke, hvilket fag han er i
Han var en ekspert, selvom han var streng i ord,
Men djævelen hader ham for at dømme verden:
Prøv at dømme støvler!

Lad os analysere denne lignelse. Digtet består af 13 linjer. Den har to semantiske dele: den første på 8 linjer og den anden (lignelsens morale) på 5 linjer (13, 8, 5 er Fibonacci-tal).

Et af Pushkins sidste digte, "I value loud rights not dearly..." består af 21 linjer og har to semantiske dele: 13 og 8 linjer.

Jeg værdsætter ikke højlydte rettigheder højt,
Hvilket får mere end et hoved til at dreje.
Jeg klager ikke over, at guderne nægtede
Det er min søde skæbne at udfordre skatter
Eller forhindre konger i at kæmpe mod hinanden;
Og det er ikke nok for mig at bekymre mig, hvis pressen er fri
Dumme idioter eller følsom censur
I bladplaner er jokeren flov.
Alt dette, ser du, er ord, ord, ord.
Andre, bedre rettigheder er mig kære:
Jeg har brug for en anden, bedre frihed:
Afhængig af kongen, afhængig af folket -
Er vi ligeglade? Gud være med dem.
Ingen
Giv ikke en rapport, kun til dig selv
At tjene og behage; for magt, for livry
Bøj ikke din samvittighed, dine tanker, din nakke;
At vandre her og der efter behag,
Forundres over naturens guddommelige skønhed,
Og før kreationerne af kunst og inspiration
Rystende frydefuldt i ømhedens henrykkelse,
Hvilken lykke! Det er rigtigt...

Det er karakteristisk, at den første del af dette vers (13 linjer), i henhold til dets semantiske indhold, er opdelt i 8 og 5 linjer, det vil sige, at hele digtet er struktureret i henhold til lovene i den gyldne proportion.

Analysen af romanen "Eugene Onegin" lavet af N. Vasyutinsky er af utvivlsom interesse. Denne roman består af 8 kapitler, hver med et gennemsnit på omkring 50 vers. Det ottende kapitel er det mest perfekte, mest polerede og følelsesmæssigt rige. Den har 51 vers. Sammen med Eugenes brev til Tatiana (60 linjer) svarer dette nøjagtigt til Fibonacci-tallet 55!

N. Vasyutinsky udtaler:

"Kulminationen af kapitlet er Eugenes kærlighedserklæring til Tatyana - linjen "At blive bleg og forsvinde ... dette er lyksalighed!" og i den anden - 295 linjer er 1,617. Den fineste overensstemmelse med værdien af den gyldne proportion.

Lermontovs berømte digt "Borodino" er opdelt i to dele: en introduktion henvendt til fortælleren og kun optager én strofe ("Fortæl mig, onkel, det er ikke uden grund ..."), og hoveddel, der repræsenterer en uafhængig helhed, der deler sig i to lige store dele. Den første af dem beskriver forventningen til kampen med stigende spænding, den anden beskriver selve kampen med et gradvist fald i spændingen mod slutningen af digtet. Grænsen mellem disse dele er værkets kulminationspunkt og falder nøjagtigt ved inddelingen af det gyldne snit.

Hoveddelen af digtet består af 13 syv-linjers linjer, det vil sige 91 linjer. Efter at have divideret det med det gyldne snit (91:1,618 = 56,238), er vi overbevist om, at divisionspunktet er i begyndelsen af det 57. vers, hvor der er en kort sætning: "Nå, det var en dag!". Det er denne sætning, der repræsenterer "kulminationspunktet for ophidset forventning", færdiggør den første del af digtet (forventning af slaget) og åbner dens anden del (beskrivelse af slaget).

Således spiller det gyldne snit en meget betydningsfuld rolle i poesi, der fremhæver digtets klimaks.

Gyldne snit i arkitektur, skulptur, maleri, fotografi

Et af de smukkeste værker af gammel græsk arkitektur er Parthenon (5. århundrede f.Kr.).

Figurerne viser en række mønstre forbundet med det gyldne snit. Bygningens proportioner kan udtrykkes gennem forskellige potenser af tallet Ф=0,618...

På plantegningen af Parthenon kan du også se de "gyldne rektangler":

Vi kan se det gyldne snit i katedralbygningen Notre Dame af Paris(Notre Dame de Paris), og i Cheops-pyramiden:

Proportionerne af Cheops-pyramiden, templerne, basrelieffer, husholdningsartikler og smykker fra Tutankhamons grav indikerer, at egyptiske håndværkere brugte forholdet mellem den gyldne division, da de skabte dem. Den franske arkitekt Le Corbusier fandt ud af, at i relieffet fra farao Seti I's tempel i Abydos og i relieffet, der afbilder farao Ramses, svarer figurernes proportioner til værdierne af den gyldne division. Arkitekten Khesira, afbildet på et relief af en træplade fra en grav opkaldt efter ham, holder i sine hænder måleinstrumenter, hvor proportionerne af den gyldne division er registreret.

Hvad angår pyramiderne, blev ikke kun de egyptiske pyramider bygget i overensstemmelse med de perfekte proportioner af det gyldne snit; det samme fænomen blev fundet i de mexicanske pyramider. Pyramidens tværsnit viser en form, der ligner en trappe. Det første lag har 16 trin, det andet 42 trin og det tredje - 68 trin.
Disse tal er baseret på Fibonacci-forholdet som følger:

16 x 1,618 = 26

26 x 1,618 = 42

Arkitekturen i St. Basil's Cathedral har mange gyldne proportioner:

Den gyldne proportion blev brugt af mange gamle billedhuggere. Den gyldne del af statuen af Apollo Belvedere er kendt: Højden af den afbildede mand er divideret med navlestrengen i det gyldne snit.

Tilbage i renæssancen opdagede kunstnere, at ethvert billede har visse punkter, der ufrivilligt tiltrækker vores opmærksomhed, de såkaldte visuelle centre. I dette tilfælde er det lige meget, hvilket format billedet har - vandret eller lodret. Der er kun fire sådanne punkter, de deler billedstørrelsen vandret og lodret i det gyldne snit, dvs. de er placeret i en afstand på ca. 3/8 og 5/8 fra de tilsvarende kanter af planet.

Denne opdagelse blev kaldt det "gyldne forhold" af maleriet af kunstnere på den tid. Derfor, for at henlede opmærksomheden på fotografiets hovedelement, er det nødvendigt at kombinere dette element med et af de visuelle centre.

På billedet I.I. Shishkins "Ship Grove" viser motiver af det gyldne snit. Et stærkt solbelyst fyrretræ (stående i forgrunden) deler maleriets længde omtrent i det gyldne snit. Til højre for fyrretræet er en solbelyst bakke. Den deler højre side af billedet vandret i det gyldne snit. Til venstre for hovedfyren er der mange fyrretræer - hvis det ønskes, kan du med succes fortsætte med at opdele billedet i proportionerne af det gyldne snit.

Tilstedeværelsen i billedet af lyse lodrette og vandrette linjer, der deler det i forhold til det gyldne snit, giver det en karakter af balance og ro i overensstemmelse med kunstnerens intention. Når en kunstner skaber et billede med hastigt udviklende handling, bliver et sådant geometrisk kompositionsskema (med en overvægt af lodrette og vandrette) uacceptabelt.

Følelsen af dynamik og spænding viser sig måske stærkest i et andet simpelt geometrisk figur- spiraler. Multifigurkompositionen, udført i 1509 - 1510 af Raphael, da den berømte maler skabte sine fresker i Vatikanet, er kendetegnet ved handlingens dynamik og dramatik. Raphael bragte aldrig sin plan til ende, dog blev hans skitse graveret af den ukendte italienske grafiker Marcantinio Raimondi, som på baggrund af denne skitse skabte graveringen "Massacre of the Innocents".

Hvis vi i Raphaels forberedende skitse mentalt tegner linjer, der løber fra kompositionens semantiske centrum - det punkt, hvor krigerens fingre lukkede sig om barnets ankel - langs figurerne af barnet, kvinden, der holder ham tæt, krigeren med sit sværd hævet, og derefter langs figurerne af samme gruppe på de højre dele af skitsen (i figuren er disse linjer tegnet med rødt), og derefter forbinde disse stykker med en buet stiplet linje, så med meget stor nøjagtighed er en gylden spiral opnået. Dette kan kontrolleres ved at måle forholdet mellem længderne af segmenterne skåret af en spiral på lige linjer, der går gennem begyndelsen af kurven.

Det er uvist, om Raphael faktisk tegnede den gyldne spiral, da han skabte kompositionen "Massacre of the Innocents" eller kun "følte" den. Vi kan dog med tillid sige, at gravøren Raimondi så denne spiral. Dette er bevist af de nye elementer i sammensætningen, han tilføjede, og understreger vendingen af spiralen på de steder, hvor den kun er angivet med en stiplet linje. Disse elementer kan ses i Raimondis sidste gravering: brobuen, der strækker sig fra kvindens hoved, er på venstre side af kompositionen, og barnets tilbagelænede krop er i midten.

Går man videre til eksempler på det "gyldne snit" i maleriet, kan man ikke undgå at fokusere på Leonardo da Vincis arbejde. Lad os se nærmere på maleriet "La Gioconda". Sammensætningen af portrættet er baseret på "gyldne trekanter".

Moderne model forretning bruger også ideelle proportioner, fordi "alt nyt er godt glemt gammelt":

Informationskilder:

Kovalev F.V. Det gyldne snit i maleriet. K.: Vyshcha Skole, 1989.

Kepler I. Om sekskantede snefnug. - M., 1982.

Durer A. Dagbøger, breve, afhandlinger - L., M., 1957.

Tsekov-Blyant Ts Om det andet gyldne snit. - Sofia, 1983.

Stakhov A. Koder af den gyldne proportion.

Ved at skære en firkant med side a fra et rektangel bygget efter princippet om det gyldne snit får vi et nyt, mindre rektangel med samme egenskab

Gylden afsnit (gyldne proportioner, division i ekstremt og gennemsnitligt forhold, harmonisk division, Phidias tal) - opdeling af en kontinuert værdi i dele i et sådant forhold, hvor den største del er relateret til den mindre, som hele værdien er til den større. For eksempel opdeling af et segment AC i to dele på en sådan måde, at det meste AB henviser til den mindre Sol ligesom hele segmentet AC hentyder til AB(dvs. | AB| / |Sol| = |AC| / |AB|).

Denne andel er normalt angivet græsk bogstavϕ (betegnelsen τ findes også). Det er lig med:

Formlen for "gyldne harmonier", der giver talpar, der opfylder ovenstående forhold:

I tilfælde af et tal, parameteren m = 1.

I den antikke litteratur, der er kommet ned til os, er opdelingen af et segment i ekstreme og gennemsnitlige forhold (ἄκρος καὶ μέσος λόγος ) først fundet i Euklids grundstoffer (ca. 300 f.Kr.), hvor den bruges til at konstruere en regulær femkant.

C erudtrykket "gyldne snit" (tysk)goldener Schnitt) blev introduceret af den tyske matematiker Martin Ohm i 1835.

Matematiske egenskaber

Gyldne snit i en femtakket stjerne

— irrationel algebraisk tal, positiv løsning til enhver af følgende ligninger

repræsenteret ved en fortsat brøk

Til hvis passende brøker er forholdet mellem successive Fibonacci-tal. Dermed, .

I en regulær femtakkede stjerne er hvert segment divideret med et segment, der skærer det i det gyldne snit (det vil sige forholdet mellem det blå segment og det grønne såvel som det røde til det blå såvel som det grønne til violette , er lige).

Konstruktion af det gyldne snit

Her er en anden visning:

Geometrisk konstruktion

Et segments gyldne forhold AB kan konstrueres som følger: ved punktet B vinkelret på AB, læg et segment på det B.C., lig med halvdelen AB, på segmentet A.C. afsætte et segment AD, lige A.C. − C.B. og til sidst på segmentet AB afsætte et segment A.E., lige AD. Derefter

Gyldne snit og harmoni

Det er generelt accepteret, at genstande, der indeholder det "gyldne snit", af mennesker opfattes som de mest harmoniske. Proportionerne af Cheops-pyramiden, templerne, basrelieffer, husholdningsartikler og smykker fra Tutankhamons grav tyder angiveligt på, at egyptiske håndværkere brugte forholdet mellem det gyldne snit, da de skabte dem. Arkitekten Le Corbusier "fandt", at i relieffet fra farao Seti I's tempel i Abydos og i relieffet, der forestiller farao Ramses, svarer proportionerne af figurerne til værdierne af det gyldne snit. Arkitekten Khesira, afbildet på relieff af en træplade fra graven opkaldt efter ham, holder i sine hænder måleinstrumenter, hvor proportionerne af det gyldne snit er registreret. Facaden på det antikke græske tempel Parthenon har gyldne proportioner. Under dens udgravninger blev der opdaget kompasser, der blev brugt af arkitekter og billedhuggere fra den antikke verden. Det pompeianske kompas (museum i Napoli) indeholder også proportionerne af den gyldne inddeling osv. osv.

"Gyldent snit" i kunst

Golden ratio og visuelle centre

Fra og med Leonardo da Vinci brugte mange kunstnere bevidst proportionerne med det gyldne snit.

Det er kendt, at Sergei Eisenstein kunstigt konstruerede filmen Battleship Potemkin i henhold til reglerne for det "gyldne forhold". Han brækkede båndet i fem dele. for det første tre handling udfolder sig på skibet. I de sidste to - i Odessa, hvor opstanden udspiller sig. Denne overgang til byen sker præcis ved det gyldne snit. Og hver del har sin egen brud, som opstår i henhold til loven om det gyldne snit. I en ramme, scene, episode er der et vist spring i udviklingen af temaet: plot, stemning. Eisenstein mente, at da en sådan overgang er tæt på det gyldne snit, bliver den opfattet som den mest logiske og naturlige.

Et andet eksempel på brugen af Golden Ratio-reglen i kinematografi er placeringen af rammens hovedkomponenter på særlige punkter - "visuelle centre". Ofte bruges fire punkter, placeret i afstande på 3/8 og 5/8 fra de tilsvarende kanter af flyet.

Det skal bemærkes, at i ovenstående eksempler dukkede den omtrentlige værdi af "det gyldne snit" op: det er let at verificere, at hverken 3/2 eller 5/3 er lig med værdien af det gyldne snit.

Den russiske arkitekt Zholtovsky brugte også det gyldne snit.

Kritik af det gyldne snit

Der er meninger om, at betydningen af det gyldne snit i kunst, arkitektur og natur er overdrevet og bygger på fejlagtige beregninger.

Når man diskuterer de optimale billedformater for rektangler (papirstørrelser A0 og multipler, fotografiske pladestørrelser (6:9, 9:12) eller filmrammer (ofte 2:3), film- og tv-skærmstørrelser - for eksempel 3:4 eller 9:16) en række muligheder blev testet. Det viste det sig de fleste mennesker opfatter ikke guld sektionen som optimal og betragter dens proportioner som "for langstrakte".

Antal læste: 8113