Multiplikation. Multiplikation og division af rationelle tal

) og nævner for nævner (vi får produktets nævner).

Formel til at gange brøker:

For eksempel:

Før du begynder at gange tællere og nævnere, skal du kontrollere, om brøken kan reduceres. Hvis du kan reducere brøken, vil det være lettere for dig at foretage yderligere beregninger.

At dividere en almindelig brøk med en brøk.

At dividere brøker, der involverer naturlige tal.

Det er ikke så skræmmende, som det ser ud til. Som ved addition omregner vi hele tallet til en brøk med én i nævneren. For eksempel:

Multiplicer blandede fraktioner.

Regler for at gange brøker (blandet):

konvertere blandede fraktioner til ukorrekte fraktioner;
gange tællere og nævnere af brøker;
reducere fraktionen;
Hvis du får en uægte brøk, så konverterer vi den uægte brøk til en blandet brøk.

Vær opmærksom! At formere sig blandet fraktion til en anden blandet brøk, skal du først konvertere dem til form af uægte brøker og derefter gange efter multiplikationsreglen almindelige brøker.

Den anden måde at gange en brøk med et naturligt tal.

Det kan være mere praktisk at bruge den anden metode til at gange en fælles brøk med et tal.

Vær opmærksom! For at gange en brøk med et naturligt tal, skal du dividere brøkens nævner med dette tal og lade tælleren være uændret.

Fra eksemplet ovenfor er det klart, at denne mulighed er mere praktisk at bruge, når nævneren af en brøk divideres uden en rest med et naturligt tal.

Fleretagers brøker.

I gymnasiet støder man ofte på tre-etagers (eller flere) brøker. Eksempel:

For at bringe en sådan brøk til sin sædvanlige form, brug division gennem 2 punkter:

Vær opmærksom! Når man deler brøker, er rækkefølgen af division meget vigtig. Vær forsigtig, det er nemt at blive forvirret her.

Bemærk venligst For eksempel:

Når man dividerer en med en hvilken som helst brøk, vil resultatet være den samme brøk, kun omvendt:

Praktiske tips til at gange og dividere brøker:

1. Det vigtigste, når man arbejder med brøkudtryk, er nøjagtighed og opmærksomhed. Foretag alle beregninger omhyggeligt og præcist, koncentreret og klart. Det er bedre at skrive et par ekstra linjer i din kladde end at fare vild i hovedberegninger.

2. I opgaver med forskellige typer brøker - gå til form af almindelige brøker.

3. Vi reducerer alle fraktioner, indtil det ikke længere er muligt at reducere.

4. Flere etager brøkudtryk vi bringer dem i almindelig form ved hjælp af division gennem 2 punkter.

5. Divider en enhed med en brøk i dit hoved, vend blot brøken om.

I denne artikel vil vi beskæftige os med gange tal med forskellige fortegn. Her vil vi først formulere reglen for at gange positive og negative tal, begrunde den og derefter overveje anvendelsen af denne regel ved løsning af eksempler.

Sidenavigation.

Regel for at gange tal med forskellige fortegn

At multiplicere et positivt tal med et negativt tal, såvel som et negativt tal med et positivt tal, udføres som følger: reglen for at gange tal med forskellige tegn : for at gange tal med forskellige fortegn, skal du gange og sætte et minustegn foran det resulterende produkt.

Lad os skrive det ned denne regel i brevform. For ethvert positivt reelt tal a og ethvert negativt reelt tal −b er ligheden a·(−b)=−(|a|·|b|) , og også for et negativt tal −a og et positivt tal b er ligheden (−a)·b=−(|a|·|b|) .

Reglen for at gange tal med forskellige fortegn er fuldstændig i overensstemmelse med egenskaber ved operationer med reelle tal. På deres grundlag er det faktisk let at vise, at for reelle og positive tal a og b en kæde af ligheder af formen a·(−b)+a·b=a·((−b)+b)=a·0=0, hvilket beviser, at a·(−b) og a·b er modsatte tal, hvilket indebærer ligheden a·(−b)=−(a·b) . Og deraf følger gyldigheden af den pågældende multiplikationsregel.

Det skal bemærkes, at den angivne regel for at gange tal med forskellige fortegn gælder for både reelle tal og rationelle tal og for heltal. Dette følger af, at operationer med rationelle tal og heltal har de samme egenskaber, som blev brugt i beviset ovenfor.

Det er klart, at multiplikation af tal med forskellige fortegn ifølge den resulterende regel kommer ned til at gange positive tal.

Det er kun tilbage at overveje eksempler på anvendelsen af den adskilte multiplikationsregel, når man multiplicerer tal med forskellige fortegn.

Eksempler på at gange tal med forskellige fortegn

Lad os se på flere løsninger eksempler på at gange tal med forskellige fortegn. Lad os starte med en simpel case for at fokusere på reglens trin frem for den beregningsmæssige kompleksitet.

Gang det negative tal −4 med det positive tal 5.

Ifølge reglen for at gange tal med forskellige fortegn, skal vi først gange de absolutte værdier af de oprindelige faktorer. Modul −4 er lig med 4, og modul 5 er lig med 5, og multiplikation naturlige tal 4 og 5 giver 20. Til sidst er det tilbage at sætte et minustegn foran det resulterende tal, vi har -20. Dette fuldender multiplikationen.

Kort fortalt kan løsningen skrives som følger: (−4) 5=−(4 5)=−20.

(−4)·5=−20.

Når du multiplicerer brøker med forskellige fortegn, skal du kunne gange almindelige brøker, gange decimaler og deres kombinationer med naturlige og blandede tal.

Gang tal med forskellige fortegn 0, (2) og.

Efter at have udført konverteringen af en periodisk decimalbrøk til en almindelig brøk, og også efter at have udført overgangen fra et blandet tal til en uægte brøk, kommer vi fra det originale produkt til produktet af almindelige brøker med forskellige tegn på formen . Dette produkt er lig med reglen for at gange tal med forskellige fortegn. Tilbage er blot at gange de almindelige brøker i parentes, vi har .

Separat er det værd at nævne multiplikationen af tal med forskellige fortegn, når en eller begge faktorer er

Lad os nu beskæftige os med multiplikation og division.

Lad os sige, at vi skal gange +3 med -4. Hvordan gør man dette?

Lad os overveje sådan en sag. Tre personer kom i gæld og havde hver $4 i gæld. Hvad er den samlede gæld? For at finde den skal du lægge alle tre gæld sammen: 4 dollars + 4 dollars + 4 dollars = 12 dollars. Vi besluttede, at tilføjelsen af tre tal 4 betegnes som 3x4. Da vi i dette tilfælde taler om gæld, er der et "-"-tegn før 4. Vi ved, at den samlede gæld er $12, så vores problem bliver nu 3x(-4)=-12.

Vi får det samme resultat, hvis hver af de fire personer ifølge problemet har en gæld på $3. Med andre ord, (+4)x(-3)=-12. Og da rækkefølgen af faktorerne ikke betyder noget, får vi (-4)x(+3)=-12 og (+4)x(-3)=-12.

Lad os opsummere resultaterne. Når du ganger et positivt tal og et negativt tal, vil resultatet altid være et negativt tal. Den numeriske værdi af svaret vil være den samme som ved positive tal. Produkt (+4)x(+3)=+12. Tilstedeværelsen af "-" tegnet påvirker kun tegnet, men påvirker ikke den numeriske værdi.

Hvordan ganges to negative tal?

Desværre er det meget svært at komme med et passende eksempel fra det virkelige liv om dette emne. Det er let at forestille sig en gæld på 3 eller 4 dollars, men det er absolut umuligt at forestille sig -4 eller -3 personer, der kom i gæld.

Måske går vi en anden vej. I multiplikation, når tegnet for en af faktorerne ændres, ændres produktets fortegn. Hvis vi ændrer tegnene for begge faktorer, skal vi ændre to gange arbejdsmærke, først fra positiv til negativ, og derefter omvendt, fra negativ til positiv, det vil sige, at produktet vil have et indledende tegn.

Derfor er det ret logisk, selvom det er lidt mærkeligt, at (-3) x (-4) = +12.

Skilteposition når det ganges, ændres det sådan:

positivt tal x positivt tal = positivt tal;
negativt tal x positivt tal = negativt tal;
positivt tal x negativt tal = negativt tal;
negativt tal x negativt tal = positivt tal.

Med andre ord, gange to tal med de samme fortegn, får vi et positivt tal. Hvis vi multiplicerer to tal med forskellige fortegn, får vi et negativt tal.

Den samme regel gælder for handlingen modsat multiplikation - for.

Du kan nemt bekræfte dette ved at køre inverse multiplikationsoperationer. I hvert af eksemplerne ovenfor, hvis du gange kvotienten med divisor, vil du få udbyttet og sikre dig, at det har samme fortegn, for eksempel (-3)x(-4)=(+12).

Da vinteren er på vej, er det tid til at tænke over, hvad du skal skifte din jernhests sko til for ikke at glide på isen og føle dig sikker på vintervejene. Du kan for eksempel købe Yokohama dæk på hjemmesiden: mvo.ru eller nogle andre, det vigtigste er, at de er af høj kvalitet, mere information og priser kan du finde ud af på hjemmesiden Mvo.ru.

Denne artikel giver et detaljeret overblik dividere tal med forskellige fortegn. Først gives reglen for at dividere tal med forskellige fortegn. Nedenfor er eksempler på at dividere positive tal med negative og negative tal med positive.

Sidenavigation.

Regel for opdeling af tal med forskellige fortegn

I artikelinddelingen af heltal blev der opnået en regel for at dividere heltal med forskellige fortegn. Det kan udvides til både rationelle tal og reelle tal ved at gentage alle ræsonnementerne fra ovenstående artikel.

Så, regel for at dividere tal med forskellige fortegn har følgende formulering: for at dividere et positivt tal med et negativt eller et negativt tal med et positivt, skal du dividere udbyttet med divisormodulet og sætte et minustegn foran det resulterende tal.

Lad os skrive denne divisionsregel ved hjælp af bogstaver. Hvis tallene a og b har forskellige fortegn, er formlen gyldig a:b=−|a|:|b| .

Ud fra den angivne regel er det klart, at resultatet af at dividere tal med forskellige fortegn er et negativt tal. Da udbyttemodulet og divisormodulet er positive tal, er deres kvotient et positivt tal, og minustegnet gør dette tal negativt.

Bemærk, at den betragtede regel reducerer divisionen af tal med forskellige fortegn til divisionen af positive tal.

Du kan give en anden formulering af reglen for at dividere tal med forskellige fortegn: For at dividere tallet a med tallet b, skal du gange tallet a med tallet b −1, det omvendte af tallet b. det vil sige a:b=a b −1 .

Denne regel kan bruges, når det er muligt at gå ud over sættet af heltal (da ikke hvert heltal har en invers). Med andre ord gælder det for mængden af rationelle tal såvel som for mængden af reelle tal.

Det er klart, at denne regel for at dividere tal med forskellige fortegn giver dig mulighed for at gå fra division til multiplikation.

Den samme regel bruges ved dividering af negative tal.

Det er tilbage at overveje, hvordan denne regel for at dividere tal med forskellige tegn anvendes ved løsning af eksempler.

Eksempler på opdeling af tal med forskellige fortegn

Lad os overveje løsninger på flere karakteristika eksempler på opdeling af tal med forskellige fortegn at forstå princippet om at anvende reglerne fra det foregående afsnit.

Divider det negative tal -35 med det positive tal 7.

Reglen for at dividere tal med forskellige fortegn foreskriver først at finde modulerne for udbytte og divisor. Modulet for -35 er 35, og modulet for 7 er 7. Nu skal vi dividere modulet af udbytte med modulet af divisor, det vil sige, vi skal dividere 35 med 7. Når vi husker, hvordan division af naturlige tal udføres, får vi 35:7=5. Det sidste trin tilbage i reglen for at dividere tal med forskellige fortegn er at sætte et minus foran det resulterende tal, vi har −5.

Her er hele løsningen: .

Det var muligt at gå ud fra en anden formulering af reglen for at dividere tal med forskellige fortegn. I dette tilfælde finder vi først det omvendte af divisor 7. Dette tal er den almindelige brøk 1/7. Således,. Det er tilbage at gange tal med forskellige fortegn: . Det er klart, at vi kom til det samme resultat.

(−35):7=−5 .

Beregn kvotienten 8:(−60) .

Ifølge reglen for at dividere tal med forskellige fortegn, har vi 8:(−60)=−(|8|:|−60|)=−(8:60) . Det resulterende udtryk svarer til en negativ almindelig brøk (se divisionstegnet som en brøklinje), du kan reducere brøken med 4, vi får .

Lad os kort skrive hele løsningen ned: .

Når man dividerer rationelle brøktal med forskellige fortegn, er deres udbytte og divisor normalt repræsenteret som almindelige brøker. Dette skyldes det faktum, at det ikke altid er praktisk at udføre division med tal i anden notation (for eksempel i decimal).

Udbyttemodulet er lig, og divisormodul er 0,(23) . For at dividere udbyttemodulet med divisormodulet, lad os gå videre til almindelige brøker.

I denne lektion Multiplikation og division af rationelle tal overvejes.

Lektionens indhold

Multiplikation af rationelle tal

Reglerne for multiplikation af heltal gælder også for rationelle tal. Med andre ord, for at gange rationelle tal skal du være i stand til det

Du skal også kende de grundlæggende love for multiplikation, såsom: den kommutative lov for multiplikation, den associative lov for multiplikation, den distributive lov for multiplikation og multiplikation med nul.

Eksempel 1. Find værdien af et udtryk

Dette er multiplikationen af rationelle tal med forskellige fortegn. For at gange rationelle tal med forskellige tegn skal du gange deres moduler og sætte et minus foran det resulterende svar.

For tydeligt at se, at vi har at gøre med tal, der har forskellige fortegn, indsætter vi hvert rationelt tal i parentes sammen med dets tegn

Modulus af tallet er lig med , og modul af tallet er lig med . Efter at have ganget de resulterende moduler som positive brøker, modtog vi svaret, men før svaret satte vi et minus, som reglen krævede af os. For at sikre dette minus før svaret, blev multiplikationen af moduler udført i parentes, efterfulgt af et minus.

Den korte løsning ser således ud:

Eksempel 2. Find værdien af et udtryk

Eksempel 3. Find værdien af et udtryk

Dette er multiplikationen af negative rationale tal. For at gange negative rationelle tal skal du gange deres moduler og sætte et plus foran det resulterende svar

Løsning til dette eksempel kan skrives kort:

Eksempel 4. Find værdien af et udtryk

Løsningen til dette eksempel kan kort skrives:

Eksempel 5. Find værdien af et udtryk

Dette er multiplikationen af rationelle tal med forskellige fortegn. Lad os gange modulerne af disse tal og sætte et minus foran det resulterende svar

Den korte løsning vil se meget enklere ud:

Eksempel 6. Find værdien af et udtryk

Lad os konvertere det blandede tal til en uægte brøk. Lad os omskrive resten, som det er

Vi opnåede multiplikationen af rationelle tal med forskellige fortegn. Lad os gange modulerne af disse tal og sætte et minus foran det resulterende svar. Indgangen med moduler kan springes over for ikke at rode i udtrykket

Løsningen til dette eksempel kan skrives kort

Eksempel 7. Find værdien af et udtryk

Dette er multiplikationen af rationelle tal med forskellige fortegn. Lad os gange modulerne af disse tal og sætte et minus foran det resulterende svar

Først viste svaret sig at være en ukorrekt brøk, men vi fremhævede hele delen i det. bemærk det hele delen blev adskilt fra fraktionsmodulet. Det resulterende blandede tal blev omgivet af parentes foran af et minustegn. Dette gøres for at sikre, at reglens krav er opfyldt. Og reglen krævede, at det modtagne svar blev indledt med et minus.

Løsningen til dette eksempel kan kort skrives:

Eksempel 8. Find værdien af et udtryk

Lad os først gange og og gange det resulterende tal med det resterende tal 5. Vi springer indgangen over med moduler for ikke at rode i udtrykket.

Svar: udtryksværdi er lig med -2.

Eksempel 9. Find betydningen af udtrykket:

Lad os oversætte blandede tal til uægte brøker:

Vi fik multiplikationen af negative rationale tal. Lad os gange modulerne af disse tal og sætte et plus foran det resulterende svar. Indgangen med moduler kan springes over for ikke at rode i udtrykket

Eksempel 10. Find værdien af et udtryk

Udtrykket består af flere faktorer. Ifølge den associative lov om multiplikation, hvis et udtryk består af flere faktorer, vil produktet ikke afhænge af rækkefølgen af handlinger. Dette giver os mulighed for at evaluere et givet udtryk i vilkårlig rækkefølge.

Lad os ikke genopfinde hjulet, men beregne dette udtryk fra venstre mod højre i rækkefølgen af faktorerne. Lad os springe posten over med moduler for ikke at rode i udtrykket

Tredje handling:

Fjerde handling:

Svar: værdien af udtrykket er

Eksempel 11. Find værdien af et udtryk

Lad os huske loven om multiplikation med nul. Denne lov siger, at et produkt er lig nul, hvis mindst en af faktorerne er lig nul.

I vores eksempel er en af faktorerne lig nul, så uden at spilde tid svarer vi, at værdien af udtrykket er lig nul:

Eksempel 12. Find værdien af et udtryk

Produktet er lig nul, hvis mindst en af faktorerne er lig nul.

I vores eksempel er en af faktorerne lig nul, så uden at spilde tid svarer vi, at værdien af udtrykket er lig med nul:

Eksempel 13. Find værdien af et udtryk

Du kan bruge rækkefølgen af handlinger og først beregne udtrykket i parentes og gange det resulterende svar med en brøk.

Du kan også bruge den distributive lov om multiplikation - gange hvert led af summen med en brøk og tilføj de resulterende resultater. Vi vil bruge denne metode.

Ifølge rækkefølgen af operationer, hvis et udtryk indeholder addition og multiplikation, skal multiplikationen udføres først. Lad os derfor i det resulterende nye udtryk sætte de parametre i parentes, der skal ganges. På denne måde kan vi tydeligt se, hvilke handlinger der skal udføres tidligere og hvilke senere:

Tredje handling:

Svar: udtryksværdi lig med

Løsningen til dette eksempel kan skrives meget kortere. Det vil se sådan ud:

Det er klart, at dette eksempel kunne løses selv i ens sind. Derfor bør du udvikle evnen til at analysere et udtryk, før du løser det. Det er sandsynligt, at det kan løses mentalt og spare en masse tid og nerver. Og i prøver og eksamener er tid som bekendt meget værdifuld.

Eksempel 14. Find værdien af udtrykket −4,2 × 3,2

Dette er multiplikationen af rationelle tal med forskellige fortegn. Lad os gange modulerne af disse tal og sætte et minus foran det resulterende svar

Læg mærke til, hvordan modulerne af rationelle tal blev ganget. I dette tilfælde, for at gange modulerne af rationelle tal, tog det .

Eksempel 15. Find værdien af udtrykket −0,15 × 4

Dette er multiplikationen af rationelle tal med forskellige fortegn. Lad os gange modulerne af disse tal og sætte et minus foran det resulterende svar

Læg mærke til, hvordan modulerne af rationelle tal blev ganget. I dette tilfælde, for at gange modulerne af rationelle tal, var det nødvendigt at kunne.

Eksempel 16. Find værdien af udtrykket −4,2 × (−7,5)

Dette er multiplikationen af negative rationale tal. Lad os gange modulerne af disse tal og sætte et plus foran det resulterende svar

Division af rationelle tal

Reglerne for at dividere heltal gælder også for rationelle tal. Med andre ord, for at kunne dividere rationelle tal, skal du være i stand til det

Ellers bruges de samme metoder til at dividere almindelige og decimalbrøker. For at dividere en fælles brøk med en anden brøk, skal du gange den første brøk med den gensidige brøk af den anden brøk.

Og for at dividere en decimalbrøk i en anden decimalbrøk, skal du flytte decimaltegnet i udbyttet og i divisoren til højre med lige så mange cifre, som der er efter decimaltegnet i divisoren, og derefter udføre divisionen som med en almindeligt nummer.

Eksempel 1. Find betydningen af udtrykket:

Dette er divisionen af rationelle tal med forskellige fortegn. For at beregne et sådant udtryk skal du gange den første brøk med den gensidige af den anden.

Så lad os gange den første brøk med den gensidige af den anden.

Vi opnåede multiplikationen af rationelle tal med forskellige fortegn. Og vi ved allerede, hvordan man beregner sådanne udtryk. For at gøre dette skal du gange modulerne af disse rationelle tal og sætte et minus foran det resulterende svar.

Lad os fuldføre dette eksempel til ende. Indgangen med moduler kan springes over for ikke at rode i udtrykket

Så værdien af udtrykket er

Den detaljerede løsning er som følger:

En kort løsning ville se sådan ud:

Eksempel 2. Find værdien af et udtryk

Dette er divisionen af rationelle tal med forskellige fortegn. For at beregne dette udtryk skal du gange den første brøk med den gensidige af den anden.

Den gensidige af den anden fraktion er . Lad os gange den første brøk med den:

En kort løsning ville se sådan ud:

Eksempel 3. Find værdien af et udtryk

Dette er divisionen af negative rationale tal. For at beregne dette udtryk skal du igen gange den første brøk med den gensidige af den anden.

Den gensidige af den anden fraktion er . Lad os gange den første brøk med den:

Vi fik multiplikationen af negative rationale tal. Vi ved allerede, hvordan et sådant udtryk beregnes. Du skal gange modulerne af rationelle tal og sætte et plus foran det resulterende svar.

Lad os afslutte dette eksempel til ende. Du kan springe posten over med moduler for ikke at rode med udtrykket:

Eksempel 4. Find værdien af et udtryk

For at beregne dette udtryk skal du gange det første tal −3 med den omvendte brøkdel af .

Det omvendte af en brøk er brøken. Gang det første tal −3 med det

Eksempel 6. Find værdien af et udtryk

For at beregne dette udtryk skal du gange den første brøk med tallet gensidig af antallet 4.

Den gensidige af tallet 4 er en brøkdel. Gang den første brøk med den

Eksempel 5. Find værdien af et udtryk

For at beregne dette udtryk skal du gange den første brøk med det inverse af -3

Det omvendte af −3 er en brøk. Lad os gange den første brøk med den:

Eksempel 6. Find værdien af udtrykket −14,4: 1,8

Dette er divisionen af rationelle tal med forskellige fortegn. For at beregne dette udtryk skal du dividere udbyttemodulet med divisormodulet og sætte et minus før det resulterende svar

Læg mærke til, hvordan udbyttemodulet blev divideret med divisormodulet. I dette tilfælde, for at gøre det korrekt, var det nødvendigt at kunne.

Hvis du ikke vil rode rundt med decimaler (og det sker ofte), så konverter disse blandede tal til uægte brøker og lav så selve divisionen.

Lad os beregne det foregående udtryk −14,4: 1,8 på denne måde. Lad os konvertere decimaler til blandede tal:

Lad os nu konvertere de resulterende blandede tal til uægte brøker:

Nu kan du lave division direkte, nemlig dividere en brøk med en brøk. For at gøre dette skal du gange den første brøk med den omvendte brøkdel af den anden:

Eksempel 7. Find værdien af et udtryk

Lad os konvertere decimalbrøken −2,06 til en uegen brøk og gange denne brøk med den reciproke af den anden brøk:

Fleretagers brøker

Man kan ofte støde på et udtryk, hvor brøkdelingen er skrevet ved hjælp af en brøklinje. For eksempel kan udtrykket skrives som følger:

Hvad er forskellen mellem udtrykkene og ? Der er virkelig ingen forskel. Disse to udtryk har samme betydning, og vi kan sætte et lighedstegn mellem dem:

I det første tilfælde er divisionstegnet et kolon, og udtrykket er skrevet på én linje. I det andet tilfælde skrives brøkdelingen ved hjælp af en brøklinje. Resultatet er en brøkdel, som folk er enige om at ringe til flere etager.

Når du støder på sådanne flerhistorieudtryk, skal du anvende de samme regler for at dividere almindelige brøker. Den første brøk skal ganges med den gensidige af den anden.

Det er ekstremt ubelejligt at bruge sådanne brøker i en løsning, så du kan skrive dem i en forståelig form ved at bruge et kolon frem for en brøklinje som et divisionstegn.

Lad os for eksempel skrive en brøk med flere etager i en forståelig form. For at gøre dette skal du først finde ud af, hvor den første brøk er, og hvor den anden er, fordi det ikke altid er muligt at gøre dette korrekt. Fleretagers brøker har flere brøklinjer, der kan være forvirrende. Hovedbrøklinjen, som adskiller den første fraktion fra den anden, er normalt længere end resten.

Efter at have bestemt hovedbrøklinjen, kan du nemt forstå, hvor den første brøk er, og hvor den anden er:

Eksempel 2.

Vi finder hovedbrøklinjen (den er den længste) og ser, at hele tallet −3 er divideret med en fællesbrøk

Og hvis vi ved en fejl tog den anden brøklinje som den førende (den der er kortere), så ville det vise sig, at vi dividerer brøken med det helt tal 5. I dette tilfælde, selvom dette udtryk er beregnet korrekt, problem vil blive løst forkert, da udbyttet i dette I dette tilfælde er tallet −3, og divisoren er brøken .

Eksempel 3. Lad os skrive brøken på flere niveauer i en forståelig form

Vi finder hovedbrøklinjen (den er den længste) og ser at brøken er divideret med hele tallet 2

Og hvis vi ved en fejl tog den første brøklinje som den førende (den der er kortere), så ville det vise sig, at vi dividerer hele tallet −5 med brøken, selv hvis dette udtryk er beregnet korrekt. problemet vil blive løst forkert, da udbyttet i dette tilfælde er brøken , og divisoren er hele tallet 2.

På trods af at brøker på flere niveauer er ubelejlige at arbejde med, vil vi støde på dem meget ofte, især når vi studerer højere matematik.

Naturligvis tager det ekstra tid og plads at omsætte en brøkdel af flere etager til en forståelig form. Derfor kan du bruge mere hurtig metode. Denne metode er praktisk, og outputtet giver dig mulighed for at få et færdigt udtryk, hvor den første fraktion allerede er ganget med den gensidige fraktion af den anden.

Denne metode implementeres som følger:

Hvis brøken for eksempel er fire-etagers, så hæves tallet på første sal til øverste etage. Og figuren placeret på anden sal er hævet til tredje sal. De resulterende tal skal forbindes med multiplikationstegn (×)

Som et resultat, uden om den mellemliggende notation, får vi et nyt udtryk, hvor den første brøk allerede er blevet ganget med den gensidige brøk af den anden. Bekvemmelighed og det er det!

For at undgå fejl, når du bruger denne metode, kan du følge følgende regel:

Fra første til fjerde. Fra anden til tredje.

I reglen vi taler om om gulvene. Figuren fra første sal skal hæves til fjerde sal. Og figuren fra anden sal skal hæves til tredje sal.

Lad os prøve at beregne en brøk med flere etager ved hjælp af ovenstående regel.

Så vi hæver tallet på første sal til fjerde sal og hæver tallet på anden sal til tredje sal

Som et resultat, uden om den mellemliggende notation, får vi et nyt udtryk, hvor den første brøk allerede er blevet ganget med den gensidige brøk af den anden. Dernæst kan du bruge din eksisterende viden:

Lad os prøve at beregne en brøk på flere niveauer ved hjælp af et nyt skema.

Der er kun første, anden og fjerde sal. Der er ingen tredje sal. Men vi afviger ikke fra grundordningen: vi hæver figuren fra første sal til fjerde sal. Og da der ikke er nogen tredje sal, lader vi nummeret ligge på anden sal som det er

Som et resultat, uden om den mellemliggende notation, modtog vi et nyt udtryk, hvor det første tal −3 allerede er blevet ganget med den gensidige brøkdel af det andet. Dernæst kan du bruge din eksisterende viden:

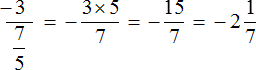
Lad os prøve at beregne brøken med flere etager ved hjælp af det nye skema.

Der er kun anden, tredje og fjerde etage. Der er ingen første sal. Da der ikke er nogen første sal, er der ikke noget at gå op til fjerde sal, men vi kan hæve figuren fra anden sal til tredje:

Som et resultat, uden om den mellemliggende notation, modtog vi et nyt udtryk, hvor den første brøk allerede er blevet ganget med den inverse af divisor. Dernæst kan du bruge din eksisterende viden:

Brug af variabler

Hvis udtrykket er komplekst, og det forekommer dig, at det vil forvirre dig i processen med at løse problemet, så kan en del af udtrykket lægges ind i en variabel og derefter arbejde med denne variabel.

Matematikere gør ofte dette. Et komplekst problem opdeles i lettere delopgaver og løses. Derefter samles de løste delopgaver i én enkelt helhed. Denne kreativ proces og det er noget man lærer gennem årene gennem hård træning.

Brugen af variable er berettiget, når man arbejder med brøker på flere niveauer. For eksempel:

Find værdien af et udtryk

Så der er et brøkudtryk i tælleren, og i hvis nævner der er brøkudtryk. Med andre ord står vi igen med en etagebrøk, som vi ikke bryder os så meget om.

Udtrykket i tælleren kan indtastes i en variabel med et hvilket som helst navn, for eksempel:

Men i matematik er det i et sådant tilfælde sædvanligt at navngive variabler med store latinske bogstaver. Lad os ikke bryde denne tradition og markere det første udtryk med et stort latinsk bogstav EN

Og udtrykket i nævneren kan betegnes med stort B

Nu tager vores oprindelige udtryk formen. Det vil sige, at vi lavede en udskiftning numerisk udtryk til et bogstav, efter at have indtastet tæller og nævner i variablerne A og B.

Nu kan vi separat beregne værdierne af variabel A og værdien af variabel B. Vi vil indsætte de færdige værdier i udtrykket.

Lad os finde værdien af variablen EN

Lad os finde værdien af variablen B

Lad os nu erstatte deres værdier i hovedudtrykket i stedet for variable A og B:

Vi har opnået en brøk med flere etager, hvor vi kan bruge skemaet "fra første til fjerde, fra anden til tredje", det vil sige hæve tallet på første sal til fjerde sal og hæve nummer placeret på anden sal til tredje sal. Yderligere beregninger vil ikke være vanskelige:

Værdien af udtrykket er således −1.

Vi har selvfølgelig overvejet enkleste eksempel, men vores mål var at lære, hvordan vi kan bruge variabler til at gøre tingene lettere for os selv, for at minimere muligheden for fejl.

Bemærk også, at løsningen til dette eksempel kan skrives uden brug af variable. Det vil se ud

Denne løsning er hurtigere og kortere, og i dette tilfælde giver det mere mening at skrive det på denne måde, men hvis udtrykket viser sig at være komplekst, bestående af flere parametre, parenteser, rødder og potenser, så er det tilrådeligt at beregne det i flere stadier, indtastning af en del af dets udtryk i variabler.

Kunne du lide lektionen?
Deltag i vores ny gruppe VKontakte og begynd at modtage meddelelser om nye lektioner

Lektionens mål:

Pædagogisk:

formulere regler for multiplikation af tal med de samme og forskellige fortegn;
mestre og forbedre færdighederne i at gange tal med forskellige fortegn.

Uddannelsesmæssigt:

udvikling af mentale operationer: sammenligning, generalisering, analyse, analogi;
kompetenceudvikling selvstændigt arbejde;
udvider elevernes horisont.

Pædagogisk:

fremme af en journalføringskultur;
uddannelse af ansvar, opmærksomhed;
skabe interesse for emnet.

Lektionstype: lære nyt stof.

Udstyr: computer, multimedieprojektor, kort til spillet “Mathematical Combat”, tests, videnskort.

Plakater på væggene:

Viden er den mest fremragende af ejendele. Alle stræber efter det, men det kommer ikke af sig selv.
Al-Biruni
I alt ønsker jeg at komme til selve essensen...
B. Pasternak

Lektionsplan

Organisatorisk øjeblik (1 min).
Indledende tale ved lærer (3 min).
Mundtligt arbejde (10 min).
Præsentation af materialet (15 min).
Matematisk kæde (5 min).
Lektier(2 min).
Test (6 min).
Lektionsresumé (3 min).

Lektionens fremskridt

I. Organisatorisk øjeblik

elevernes parathed til undervisningen.

II. Lærerens åbningstale

Gutter, vi mødtes med jer i dag ikke forgæves, men for frugtbart arbejde: at få viden.

Siden universet har eksisteret,
Der er ingen, der ikke har brug for viden.
Uanset hvilket sprog og alder vi vælger,
Mennesket har altid stræbt efter viden...
Rudaki

I klassen vil vi studere nyt materiale, konsolider det, arbejd selvstændigt, evaluer dig selv og dine kammerater. Alle har et videnskort på deres skrivebord, hvor vores lektion er opdelt i etaper. De point du har optjent på forskellige stadier du vil selv indtaste lektionen på dette kort. Og i slutningen af lektionen vil vi opsummere. Placer disse kort på et synligt sted.

III. Mundtligt arbejde (i form af spillet "Mathematical Combat")

Gutter, før vi starter nyt emne, lad os gentage det, vi lærte tidligere. Alle har et ark papir med spillet "Mathematical Combat" på deres skrivebord. De lodrette og vandrette kolonner indeholder de tal, der skal tilføjes. Disse tal er markeret med prikker. Vi vil skrive svarene i de celler på feltet, hvor prikkerne er.

Tre minutter at fuldføre. Vi startede arbejdet.

Nu udvekslede vi værker med vores skrivebordsnabo og tjekker dem med hinanden. Hvis du mener, at svaret er forkert, så streg det forsigtigt ud og skriv det rigtige ved siden af. Lad os tjekke.

Lad os nu tjekke svarene med skærmen ( De rigtige svar projiceres på skærmen).

For korrekt løst

5 opgaver gives 5 point;
4 opgaver – 4 point;
3 opgaver – 3 point;
2 opgaver – 2 point;
1 opgave – 1 point.

Godt gået. De lagde alt til side. Gutter, lad os indtaste antallet af scorede point for "Matematisk kamp" på vores videnskort ( Bilag 1).

IV. Præsentation af materialet

Åbn projektmapperne. Skriv nummeret ned, godt arbejde.

Hvilke operationer på positive og negative tal kender du?
Hvordan tilføjer man to negative tal?
Hvordan tilføjer man to tal med forskellige fortegn?
Hvordan trækker man tal med forskellige fortegn?
Du bruger altid ordet "modul". Hvad er modulet af et tal? EN?

Dagens lektionsemne er også relateret til betjeningen af antallet af forskellige tegn. Men det var gemt i et anagram, hvor du skal bytte bogstaver og få et velkendt ord. Lad os prøve at finde ud af det.

ENOZHEUMNI

Vi skriver emnet for lektionen ned: "Multiplikation."

Formålet med vores lektion: at blive bekendt med multiplikationen af positive og negative tal og formulere regler for at gange tal med både samme og forskellige fortegn.

Al opmærksomhed til bestyrelsen. Før du er en tabel med problemer, løse som vi vil formulere reglerne for at gange positive og negative tal.

2*3 = 6°C;
–2*3 = –6°С;
–2*(–3) = 6°С;
2*(–3) = –6°С;

1. Lufttemperaturen stiger med 2°C hver time. Nu viser termometeret 0°C ( Bilag 2- Termometer) (slide 1 på computeren).

Hvor meget modtog du?(6 ° MED).
Nogen vil skrive løsningen på tavlen, og vi er alle i notesbøger.
Lad os se på termometeret, fik vi det rigtige svar? (slide 2 på computeren).

2. Lufttemperaturen falder med 2°C hver time. Termometeret viser nu 0°C (slide 3 på computeren). Hvilken lufttemperatur vil termometeret vise efter 3 timer?

Hvor meget modtog du?(–6 ° MED).
Vi skriver den tilsvarende løsning ned på tavlen og i notesbøger. Analogi med opgave 1.
.(slide 4 på computeren).

3. Lufttemperaturen falder med 2°C hver time. Termometeret viser nu 0°C (slide 5 på computeren).

Hvor meget modtog du?(6 ° MED).
Vi skriver den tilsvarende løsning ned på tavlen og i notesbøger. Analogi med opgave 1 og 2.
Lad os sammenligne resultatet med termometeraflæsningen.(slide 6 på computeren).

4. Lufttemperaturen stiger med 2°C hver time. Termometeret viser nu 0°C (slide 7 på computeren). Hvilken lufttemperatur viste termometeret for 3 timer siden?

Hvor meget modtog du?(–6 ° MED).
Vi skriver den tilsvarende løsning ned på tavlen og i notesbøger. Analogi med opgave 1-3.
Lad os sammenligne resultatet med termometeraflæsningen.(slide 8 på computeren).

Se på dine resultater. Når du gangede tal med de samme fortegn (eksempel 1 og 3), hvilket tegn fik du svaret? (positiv).

Bøde. Men i eksempel 3 er begge faktorer negative, og svaret er positivt. Hvilket matematisk begreb giver dig mulighed for at gå fra negative tal til positive? (modul).

Opmærksomhedsregel: For at gange to tal med de samme fortegn, skal du gange deres absolutte værdier og sætte et plustegn foran resultatet. (2 personer gentager).

Lad os vende tilbage til eksempel 3. Hvad er modulerne (–2) og (–3) lig med? Lad os multiplicere disse moduler. Hvor meget modtog du? Med hvilket skilt?

Når du gangede tal med forskellige fortegn (eksempel 2 og 4), hvilket tegn fik du svaret? (negativ).

Formuler dine egne regler for at gange tal med forskellige fortegn.

Regel: Når du multiplicerer tal med forskellige fortegn, skal du gange deres moduler og sætte et minustegn foran resultatet. (2 personer gentager).

Lad os vende tilbage til eksempel nr. 2 og nr. 4. Hvad er størrelsen af deres faktorer? Lad os multiplicere disse moduler. Hvor meget modtog du? Hvilket tegn skal gives som et resultat?

Ved at bruge disse to regler kan du også gange brøker: decimal, blandet, alm.

Der er flere eksempler på tavlen foran dig. Vi bestemmer tre sammen med mig, og resten på egen hånd. Vær opmærksom på optagelsen og designet.

Godt gået. Lad os åbne lærebøgerne og markere de regler, der skal læres til næste lektion (side 190, §7 (punkt 35)). At kende disse regler vil hjælpe dig med hurtigt at mestre opdelingen af positive og negative tal i fremtiden.

V. Matematisk kæde

Og nu vil Dunno tjekke, hvordan du har lært det nye materiale, og vil stille dig et par spørgsmål. Vi skal skrive løsningen og svarene ned i notesbøger ( Bilag 3– Matematisk kæde).

Computer præsentation
Hej gutter. Jeg kan se, at du er meget klog og nysgerrig, så jeg vil gerne stille dig et par spørgsmål. Vær forsigtig, især med skilte.
Mit første spørgsmål er: gange (–3) med (–13).
Andet spørgsmål: gange hvad du fik i den første opgave med (–0,1).
Tredje spørgsmål: gange resultatet af den anden opgave med (–2).
Fjerde spørgsmål: gang (-1/3) med resultatet af den tredje opgave.
Og det sidste, femte spørgsmål: beregn frysepunktet for kviksølv ved at gange resultatet af den fjerde opgave med 15.
Tak for arbejdet. Jeg ønsker dig succes.

Gutter, lad os tjekke, hvordan vi fuldførte opgaverne. Alle rejste sig.

Hvor meget fik du i den første opgave?

Dem, der har et andet svar, sætter sig, og dem, der sætter sig, giver vi os selv 0 point for den matematiske kæde på vidensrekordkortet. Resten lægger ikke noget.

Hvor meget fik du i den anden opgave?

Hvis du har et andet svar, så sæt dig ned og tilføj 1 point til dit videnskort for den matematiske kæde.

Hvor meget fik du i den tredje opgave?

For dem, der har et andet svar, skal du sætte dig ned og tilføje 2 point til dit vidensrekordkort for den matematiske kæde.

Hvor meget fik du i den fjerde opgave?

For dem, der har et andet svar, skal du sætte dig ned og tilføje 3 point til dit vidensrekordkort for den matematiske kæde.

Hvor meget fik du i den femte opgave?

For dem, der har et andet svar, skal du sætte dig ned og tilføje 4 point til dit vidensrekordkort for den matematiske kæde. De resterende fyre løste alle 5 opgaver korrekt. Sæt dig ned, du giver dig selv 5 point for den matematiske kæde på dit vidensrekordkort.

Hvad er frysepunktet for kviksølv?(–39 °C).

VI. Lektier

§7 (paragraf 35, side 190), nr. 1121 – lærebog: Matematik. 6. klasse: [N.Ya.Vilenkin og andre]

Kreativ opgave: Skriv en opgave om at gange positive og negative tal.

VII. Prøve

Lad os gå videre til næste trin i lektionen: udførelse af testen ( Bilag 4).

Du skal løse opgaverne og sætte en ring om nummeret på det rigtige svar. For de første to korrekt udførte opgaver får du 1 point, for 3. opgave - 2 point, for 4. opgave - 3 point. Vi startede arbejdet.

Δ –1 point;
o –2 point;
-3 point.

Lad os nu skrive tallene på de rigtige svar ned i tabellen under testen. Lad os tjekke resultaterne. Du bør få tallet 1418 i de tomme celler (jeg skriver på tavlen). Den, der har modtaget det, sætter 7 point på videnskortet. De, der lavede fejl, satte kun antallet af scorede point for korrekt udførte opgaver på videnregistreringskortet.

Den Store Store Krig varede præcis 1418 dage. Fædrelandskrig, en sejr, hvor det russiske folk kom til en høj pris. Og den 9. maj 2010 fejrer vi 65-året for sejren over Nazityskland.

VIII. Lektionsopsummering

Lad os nu tælle samlet mængde De point, du har opnået for lektionen, og resultaterne vil blive indtastet på kortet for elevviden. Så deler vi disse kort ud.