Equazione della tangente al grafico di una funzione

P. Romanov, T. Romanova,
Magnitogorsk,
Regione di Chelyabinsk

Equazione della tangente al grafico di una funzione

L'articolo è stato pubblicato con il sostegno di ITAKA+ Hotel Complex. Soggiornando nella città dei costruttori navali Severodvinsk, non incontrerai il problema di trovare alloggi temporanei. , In linea complesso alberghiero“ITAKA+” http://itakaplus.ru, puoi affittare facilmente e velocemente un appartamento in città, per qualsiasi periodo di tempo, con un pagamento giornaliero.

SU palcoscenico moderno sviluppo dell'istruzione, uno dei suoi compiti principali è la formazione di una personalità dal pensiero creativo. La capacità di creatività negli studenti può essere sviluppata solo se sono sistematicamente coinvolti nelle basi delle attività di ricerca. La base affinché gli studenti possano utilizzare i propri poteri creativi, abilità e talenti è costituita da conoscenze e abilità a tutti gli effetti. A questo proposito, non ha poca importanza il problema della formazione di un sistema di conoscenze e abilità di base per ciascun argomento del corso di matematica scolastica. Allo stesso tempo, le competenze a tutti gli effetti dovrebbero essere l'obiettivo didattico non dei compiti individuali, ma di un loro sistema attentamente studiato. Nel senso più ampio, un sistema è inteso come un insieme di elementi interagenti e interconnessi con integrità e una struttura stabile.

Consideriamo una tecnica per insegnare agli studenti come scrivere un'equazione per una tangente al grafico di una funzione. In sostanza, tutti i problemi nella ricerca dell'equazione tangente si riducono alla necessità di selezionare da un insieme (fascio, famiglia) di linee quelle che soddisfano un determinato requisito: sono tangenti al grafico di una determinata funzione. In questo caso l'insieme delle righe da cui effettuare la selezione può essere specificato in due modi:

a) un punto giacente sul piano xOy (matita centrale delle linee);
b) coefficiente angolare (raggio parallelo di rette).

A questo proposito, studiando l’argomento “Tangente al grafico di una funzione” per isolare gli elementi del sistema, abbiamo individuato due tipologie di problemi:

1) problemi su una tangente data dal punto per cui passa;
2) problemi su una tangente dati dalla sua pendenza.

La formazione sulla risoluzione dei problemi tangenti è stata svolta utilizzando l'algoritmo proposto da A.G. Mordkovich. Il suo differenza fondamentale da quelli già noti è che l'ascissa del punto di tangenza è indicata con la lettera a (invece di x0), e quindi l'equazione della tangente assume la forma

y = f(a) + f "(a)(x – a)

(confrontare con y = f(x 0) + f "(x 0)(x – x 0)). Questo tecnica metodica, a nostro avviso, consente agli studenti di capire rapidamente e facilmente dove sono scritte le coordinate del punto corrente nell'equazione generale della tangente e dove si trovano i punti tangenti.

Algoritmo per comporre l'equazione tangente al grafico della funzione y = f(x)

1. Designare l'ascissa del punto tangente con la lettera a.
2. Trova f(a).
3. Trova f "(x) e f "(a).
4. Sostituisci i numeri trovati a, f(a), f "(a) in equazione generale tangente y = f(a) = f "(a)(x – a).

Questo algoritmo può essere compilato sulla base dell’identificazione indipendente delle operazioni da parte degli studenti e della sequenza della loro implementazione.

La pratica ha dimostrato che la soluzione sequenziale di ciascuno dei problemi chiave utilizzando un algoritmo consente di sviluppare le capacità di scrivere l'equazione di una tangente al grafico di una funzione in più fasi e i passaggi dell'algoritmo servono come punti di riferimento per le azioni . Questo approccio corrisponde alla teoria della formazione graduale delle azioni mentali sviluppata da P.Ya. Galperin e N.F. Talizina.

Nel primo tipo di compiti, sono stati individuati due compiti chiave:

• la tangente passa per un punto giacente sulla curva (problema 1);
• la tangente passa per un punto che non giace sulla curva (problema 2).

Attività 1. Scrivi un'equazione per la tangente al grafico della funzione nel punto M(3; – 2).

Soluzione. Il punto M(3; – 2) è un punto tangente, poiché

1. a = 3 – ascissa del punto tangente.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – equazione tangente.

Problema 2. Scrivi le equazioni di tutte le tangenti al grafico della funzione y = – x 2 – 4x + 2 passante per il punto M(– 3; 6).

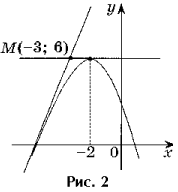Soluzione. Il punto M(– 3; 6) non è un punto tangente, poiché f(– 3) 6 (figura 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – equazione tangente.

La tangente passa per il punto M(– 3; 6), quindi le sue coordinate soddisfano l'equazione della tangente.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a2 + 6a + 8 = 0^ un 1 = – 4, un 2 = – 2.

Se a = – 4, allora l'equazione della tangente è y = 4x + 18.

Se a = – 2, l'equazione della tangente ha la forma y = 6.

Nel secondo tipo, i compiti chiave saranno i seguenti:

• la tangente è parallela ad una retta (problema 3);
• la tangente passa ad un certo angolo rispetto alla linea data (problema 4).

Problema 3. Scrivi le equazioni di tutte le tangenti al grafico della funzione y = x 3 – 3x 2 + 3, parallela alla retta y = 9x + 1.

Soluzione.

1. a – ascissa del punto tangente.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Ma, d'altra parte, f "(a) = 9 (condizione di parallelismo). Ciò significa che dobbiamo risolvere l'equazione 3a 2 – 6a = 9. Le sue radici sono a = – 1, a = 3 (Fig. 3 ).

4.1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – equazione tangente;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – equazione tangente.

Problema 4. Scrivi l'equazione della tangente al grafico della funzione y = 0,5x 2 – 3x + 1, passante con un angolo di 45° alla retta y = 0 (Fig. 4).

Soluzione. Dalla condizione f "(a) = tan 45° troviamo a: a – 3 = 1^a = 4.

1. a = 4 – ascissa del punto tangente.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – equazione tangente.

È facile dimostrare che la soluzione a qualsiasi altro problema si riduce alla risoluzione di uno o più problemi chiave. Consideriamo come esempio i due problemi seguenti.

1. Scrivi le equazioni delle tangenti alla parabola y = 2x 2 – 5x – 2, se le tangenti si intersecano ad angolo retto e una di esse tocca la parabola nel punto con ascissa 3 (Fig. 5).

Soluzione. Poiché l'ascissa del punto tangente è data, la prima parte della soluzione si riduce al problema chiave 1.

1. a = 3 – ascissa del punto di tangenza di uno dei lati dell'angolo retto.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – equazione della prima tangente.

Lascia che a – angolo di inclinazione della prima tangente. Poiché le tangenti sono perpendicolari, allora lo è l'angolo di inclinazione della seconda tangente. Dall'equazione y = 7x – 20 della prima tangente si ottiene tg a = 7. Troviamo

Ciò significa che la pendenza della seconda tangente è uguale a .

L’ulteriore soluzione si riduce al compito chiave 3.

Sia allora B(c; f(c)) il punto di tangenza della seconda retta

1. – ascissa del secondo punto di tangenza.
2.
3.
4.
– equazione della seconda tangente.

Nota. Il coefficiente angolare della tangente può essere trovato più facilmente se gli studenti conoscono il rapporto dei coefficienti delle rette perpendicolari k 1 k 2 = – 1.

2. Scrivi le equazioni di tutte le tangenti comuni ai grafici delle funzioni

Soluzione. Il compito si riduce a trovare l'ascissa dei punti di tangenza delle tangenti comuni, ovvero risolvere il problema chiave 1 in forma generale, elaborare un sistema di equazioni e quindi risolverlo (Fig. 6).

1. Sia a l'ascissa del punto tangente che giace sul grafico della funzione y = x 2 + x + 1.
2. f(a) = a2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Sia c l'ascissa del punto tangente che giace sul grafico della funzione
2.
3. f "(c) = c.
4.

Poiché le tangenti sono generali, allora

Quindi y = x + 1 e y = – 3x – 3 sono tangenti comuni.

L'obiettivo principale dei compiti considerati è preparare gli studenti a riconoscere autonomamente il tipo di problema chiave nella risoluzione di problemi più complessi che richiedono determinate capacità di ricerca (capacità di analizzare, confrontare, generalizzare, avanzare un'ipotesi, ecc.). Tali attività includono qualsiasi attività in cui l'attività chiave è inclusa come componente. Consideriamo come esempio il problema (inverso al Problema 1) di trovare una funzione dalla famiglia delle sue tangenti.

3. Per cosa sono b e c le rette y = x e y = – 2x tangenti al grafico della funzione y = x 2 + bx + c?

Soluzione.

Sia t l'ascissa del punto di tangenza della retta y = x con la parabola y = x 2 + bx + c; p è l'ascissa del punto di tangenza della retta y = – 2x con la parabola y = x 2 + bx + c. Quindi l'equazione tangente y = x assumerà la forma y = (2t + b)x + c – t 2 , e l'equazione tangente y = – 2x assumerà la forma y = (2p + b)x + c – p 2 .

Componiamo e risolviamo un sistema di equazioni

Risposta:

Problemi da risolvere in autonomia

1. Scrivi le equazioni delle tangenti disegnate sul grafico della funzione y = 2x 2 – 4x + 3 nei punti di intersezione del grafico con la retta y = x + 3.

Risposta: y = – 4x + 3, y = 6x – 9,5.

2. Per quali valori di a la tangente disegnata sul grafico della funzione y = x 2 – ax nel punto del grafico con l'ascissa x 0 = 1 passa per il punto M(2; 3)?

Risposta: a = 0,5.

3. Per quali valori di p la retta y = px – 5 tocca la curva y = 3x 2 – 4x – 2?

Risposta: p 1 = – 10, p 2 = 2.

4. Trova tutti i punti comuni del grafico della funzione y = 3x – x 3 e la tangente tracciata a questo grafico attraverso il punto P(0; 16).

Risposta: A(2; – 2), B(– 4; 52).

5. Trova la distanza più breve tra la parabola y = x 2 + 6x + 10 e la retta

Risposta:

6. Sulla curva y = x 2 – x + 1, trova il punto in cui la tangente al grafico è parallela alla retta y – 3x + 1 = 0.

Risposta: M(2; 3).

7. Scrivi l'equazione della tangente al grafico della funzione y = x 2 + 2x – | 4x |, che lo tocca in due punti. Fai un disegno.

Risposta: y = 2x – 4.

8. Dimostra che la linea y = 2x – 1 non interseca la curva y = x 4 + 3x 2 + 2x. Trova la distanza tra i loro punti più vicini.

Risposta:

9. Sulla parabola y = x 2, si prendono due punti con ascisse x 1 = 1, x 2 = 3. Attraverso questi punti si traccia una secante. In quale punto della parabola la tangente sarà parallela alla secante? Scrivi le equazioni della secante e della tangente.

Risposta: y = 4x – 3 – equazione secante; y = 4x – 4 – equazione tangente.

10. Trova l'angolo q tra le tangenti al grafico della funzione y = x 3 – 4x 2 + 3x + 1, disegnato nei punti con ascisse 0 e 1.

Risposta: q = 45°.

11. In quali punti la tangente al grafico della funzione forma un angolo di 135° con l'asse Ox?

Risposta: A(0; – 1), B(4; 3).

12. Nel punto A(1; 8) della curva viene disegnata una tangente. Trova la lunghezza del segmento tangente tra gli assi delle coordinate.

Risposta:

13. Scrivi l'equazione di tutte le tangenti comuni ai grafici delle funzioni y = x 2 – x + 1 e y = 2x 2 – x + 0,5.

Risposta: y = – 3x e y = x.

14. Trova la distanza tra le tangenti al grafico della funzione parallelo all'asse x.

Risposta:

15. Determina a quali angoli la parabola y = x 2 + 2x – 8 interseca l'asse x.

Risposta: q 1 = arctan 6, q 2 = arctan (– 6).

16. Grafico della funzione trova tutti i punti, la tangente in ciascuno dei quali a questo grafico interseca i semiassi positivi delle coordinate, tagliando da essi segmenti uguali.

Risposta: A(– 3; 11).

17. La retta y = 2x + 7 e la parabola y = x 2 – 1 si intersecano nei punti M e N. Trova il punto K di intersezione delle rette tangenti alla parabola nei punti M e N.

Risposta: K(1; – 9).

18. Per quali valori di b la retta y = 9x + b è tangente al grafico della funzione y = x 3 – 3x + 15?

Risposta 1; 31.

19. Per quali valori di k la retta y = kx – 10 ha un solo punto in comune con il grafico della funzione y = 2x 2 + 3x – 2? Per i valori trovati di k, determinare le coordinate del punto.

Risposta: k 1 = – 5, A(– 2; 0); k2 = 11, B(2; 12).

20. Per quali valori di b la tangente disegnata sul grafico della funzione y = bx 3 – 2x 2 – 4 nel punto con l'ascissa x 0 = 2 passa per il punto M(1; 8)?

Risposta: b = – 3.

21. Una parabola con vertice sull'asse del Bue tocca la retta che passa per i punti A(1; 2) e B(2; 4) nel punto B. Trova l'equazione della parabola.

Risposta:

22. A quale valore del coefficiente k la parabola y = x 2 + kx + 1 tocca l'asse del bue?

Risposta: k = d 2.

23. Trova gli angoli tra la linea retta y = x + 2 e la curva y = 2x 2 + 4x – 3.

29. Trova la distanza tra le tangenti al grafico della funzione e le generatrici con la direzione positiva dell'asse Ox con un angolo di 45°.

Risposta:

30. Trova il luogo dei vertici di tutte le parabole della forma y = x 2 + ax + b tangente alla retta y = 4x – 1.

Risposta: retta y = 4x + 3.

Letteratura

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra e inizi di analisi: 3600 problemi per gli scolari e gli iscritti all'università. – M., Otarda, 1999.
2. Mordkovich A. Seminario quattro per giovani insegnanti. Argomento: Applicazioni dei derivati. – M., “Matematica”, n. 21/94.
3. Formazione di conoscenze e abilità basate sulla teoria della graduale assimilazione delle azioni mentali. /Ed. P.Ya. Galperina, N.F. Talizina. – M., Università statale di Mosca, 1968.

Esempio 1. Data una funzione F(X) = 3X 2 + 4X– 5. Scriviamo l'equazione della tangente al grafico della funzione F(X) nel punto del grafico con l'ascissa X 0 = 1.

Soluzione. Derivata di una funzione F(X) esiste per qualsiasi x R . Troviamola:

= (3X 2 + 4X– 5)′ = 6 X + 4.

Poi F(X 0) = F(1) = 2; (X 0) = = 10. L'equazione della tangente ha la forma:

sì = (X 0) (X – X 0) + F(X 0),

sì = 10(X – 1) + 2,

sì = 10X – 8.

Risposta. sì = 10X – 8.

Esempio 2. Data una funzione F(X) = X 3 – 3X 2 + 2X+ 5. Scriviamo l'equazione della tangente al grafico della funzione F(X), parallelo alla retta sì = 2X – 11.

Soluzione. Derivata di una funzione F(X) esiste per qualsiasi x R . Troviamola:

= (X 3 – 3X 2 + 2X+ 5)′ = 3 X 2 – 6X + 2.

Poiché la tangente al grafico della funzione F(X) nel punto dell'ascissa X 0 è parallelo alla linea sì = 2X– 11, allora la sua pendenza è pari a 2, cioè ( X 0) = 2. Troviamo questa ascissa dalla condizione che 3 X– 6X 0 + 2 = 2. Questa uguaglianza è valida solo quando X 0 = 0 e a X 0 = 2. Poiché in entrambi i casi F(X 0) = 5, quindi dritto sì = 2X + B tocca il grafico della funzione nel punto (0; 5) o nel punto (2; 5).

Nel primo caso è vera l’uguaglianza numerica 5 = 2×0 + B, Dove B= 5, e nel secondo caso è vera l'uguaglianza numerica 5 = 2×2 + B, Dove B = 1.

Quindi ci sono due tangenti sì = 2X+5 e sì = 2X+ 1 al grafico della funzione F(X), parallelo alla retta sì = 2X – 11.

Risposta. sì = 2X + 5, sì = 2X + 1.

Esempio 3. Data una funzione F(X) = X 2 – 6X+ 7. Scriviamo l'equazione della tangente al grafico della funzione F(X), passando per il punto UN (2; –5).

Soluzione. Perché F(2) –5, poi punto UN non appartiene al grafico della funzione F(X). Permettere X 0 - ascissa del punto tangente.

Derivata di una funzione F(X) esiste per qualsiasi x R . Troviamola:

= (X 2 – 6X+ 1)′ = 2 X – 6.

Poi F(X 0) = X– 6X 0 + 7; (X 0) = 2X 0 – 6. L'equazione della tangente ha la forma:

sì = (2X 0 – 6)(X – X 0) + X– 6X+ 7,

sì = (2X 0 – 6)X– X+ 7.

Dal punto UN appartiene alla tangente, allora l'uguaglianza numerica è vera

–5 = (2X 0 – 6)×2– X+ 7,

Dove X 0 = 0 o X 0 = 4. Ciò significa che attraverso il punto UN puoi disegnare due tangenti al grafico della funzione F(X).

Se X 0 = 0, allora l'equazione della tangente ha la forma sì = –6X+ 7. Se X 0 = 4, allora l'equazione della tangente ha la forma sì = 2X – 9.

Risposta. sì = –6X + 7, sì = 2X – 9.

Esempio 4. Funzioni date F(X) = X 2 – 2X+2 e G(X) = –X 2 – 3. Scriviamo l'equazione della tangente comune ai grafici di queste funzioni.

Soluzione. Permettere X 1 - ascissa del punto di tangenza della retta desiderata con il grafico della funzione F(X), UN X 2 - ascissa del punto di tangenza della stessa retta con il grafico della funzione G(X).

Derivata di una funzione F(X) esiste per qualsiasi x R . Troviamola:

= (X 2 – 2X+ 2)′ = 2 X – 2.

Poi F(X 1) = X– 2X 1 + 2; (X 1) = 2X 1 – 2. L'equazione della tangente ha la forma:

sì = (2X 1 – 2)(X – X 1) + X– 2X 1 + 2,

sì = (2X 1 – 2)X – X+ 2. (1)

Troviamo la derivata della funzione G(X):

= (–X 2 – 3)′ = –2 X.

Sia data una funzione f, che in un punto x 0 ha una derivata finita f (x 0). Allora la retta passante per il punto (x 0 ; f (x 0)), avente coefficiente angolare f '(x 0), si chiama tangente.

Cosa succede se la derivata non esiste nel punto x 0? Ci sono due opzioni:

1. Non c'è nemmeno una tangente al grafico. Un classico esempio è la funzione y = |x | nel punto (0; 0).
2. La tangente diventa verticale. Questo vale ad esempio per la funzione y = arcoseno x nel punto (1; π /2).

Equazione tangente

Qualsiasi retta non verticale è data da un'equazione della forma y = kx + b, dove k è la pendenza. La tangente non fa eccezione e per comporre la sua equazione in un punto x 0 è sufficiente conoscere il valore della funzione e la derivata in questo punto.

Sia data quindi una funzione y = f (x) che ha derivata y = f ’(x) sul segmento. Allora in ogni punto x 0 ∈ (a ; b) si può tracciare una tangente al grafico di questa funzione, che è data dall'equazione:

y = f ’(x 0) (x − x 0) + f (x 0)

Qui f ’(x 0) è il valore della derivata nel punto x 0, e f (x 0) è il valore della funzione stessa.

Compito. Data la funzione y = x 3 . Scrivi un'equazione per la tangente al grafico di questa funzione nel punto x 0 = 2.

Equazione tangente: y = f ’(x 0) · (x − x 0) + f (x 0). Il punto x 0 = 2 ci è dato, ma bisognerà calcolare i valori f (x 0) e f ’(x 0).

Per prima cosa troviamo il valore della funzione. Qui è tutto facile: f (x 0) = f (2) = 2 3 = 8;
Ora troviamo la derivata: f ’(x) = (x 3)’ = 3x 2;
Sostituiamo x 0 = 2 nella derivata: f ’(x 0) = f ’(2) = 3 2 2 = 12;
In totale otteniamo: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Questa è l'equazione della tangente.

Compito. Scrivi un'equazione per la tangente al grafico della funzione f (x) = 2sen x + 5 nel punto x 0 = π /2.

Questa volta non descriveremo ogni azione nel dettaglio: indicheremo solo i passaggi chiave. Abbiamo:

f(x0) = f(π /2) = 2sin(π /2) + 5 = 2 + 5 = 7;
f '(x) = (2sen x + 5)' = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Equazione tangente:

y = 0 · (x − π /2) + 7 ⇒ y = 7

In quest'ultimo caso, la linea retta si è rivelata orizzontale, perché il suo coefficiente angolare k = 0. Non c'è niente di sbagliato in questo: ci siamo appena imbattuti in un punto estremo.

Una tangente è una linea retta , che tocca il grafico della funzione in un punto e i cui punti sono tutti alla distanza più breve dal grafico della funzione. Pertanto, la tangente passa tangente al grafico della funzione ad un certo angolo e più tangenti ad angoli diversi non possono passare attraverso il punto di tangenza. Le equazioni tangenti e le equazioni normali al grafico di una funzione vengono costruite utilizzando la derivata.

L'equazione della tangente è derivata dall'equazione della linea .

Deriviamo l'equazione della tangente e poi l'equazione della normale al grafico della funzione.

sì = kx + B .

In lui K- coefficiente angolare.

Da qui otteniamo la seguente voce:

sì - sì 0 = K(X - X 0 ) .

Valore derivato F "(X 0 ) funzioni sì = F(X) al punto X0 equivale pendenza K= tg φ tangente al grafico di una funzione passante per un punto M0 (X 0 , sì 0 ) , Dove sì0 = F(X 0 ) . Questo è significato geometrico derivato .

Quindi possiamo sostituire K SU F "(X 0 ) e ottieni quanto segue Equazione della tangente al grafico di una funzione :

sì - sì 0 = F "(X 0 )(X - X 0 ) .

Nei problemi che riguardano la composizione dell'equazione di una tangente al grafico di una funzione (e su di essi ci occuperemo tra poco), è necessario ridurre l'equazione ottenuta dalla formula precedente a Equazione di una retta in forma generale. Per fare ciò, devi spostare tutte le lettere e i numeri sul lato sinistro dell'equazione e lasciare zero sul lato destro.

Ora riguardo all'equazione normale. Normale - questa è una retta passante per il punto di tangenza al grafico della funzione perpendicolare alla tangente. Equazione normale :

(X - X 0 ) + F "(X 0 )(sì - sì 0 ) = 0

Per riscaldarti, ti viene chiesto di risolvere tu stesso il primo esempio e poi di guardare la soluzione. Ci sono tutte le ragioni per sperare che questo compito non costituisca una “doccia fredda” per i nostri lettori.

Esempio 0. Crea un'equazione tangente e un'equazione normale per il grafico di una funzione in un punto M (1, 1) .

Esempio 1. Scrivi un'equazione tangente e un'equazione normale al grafico di una funzione , se l'ascissa è tangente .

Troviamo la derivata della funzione:

Ora abbiamo tutto ciò che deve essere sostituito nella voce fornita nell'aiuto teorico per ottenere l'equazione della tangente. Noi abbiamo

In questo esempio, siamo stati fortunati: la pendenza si è rivelata pari a zero, quindi riduciamo separatamente l'equazione a aspetto generale non era necessario. Ora possiamo creare l'equazione normale:

Nella figura sotto: grafico di una funzione in colore bordeaux, tangente Colore verde, arancione normale.

Anche il prossimo esempio non è complicato: la funzione, come quella precedente, è anche un polinomio, ma la pendenza non sarà uguale a zero, quindi verrà aggiunto un ulteriore passaggio, portando l'equazione in una forma generale.

Esempio 2.

Soluzione. Troviamo l'ordinata del punto tangente:

Troviamo la derivata della funzione:

.

Troviamo il valore della derivata nel punto di tangenza, cioè la pendenza della tangente:

Sostituiamo tutti i dati ottenuti nella "formula vuota" e otteniamo l'equazione della tangente:

Portiamo l'equazione alla sua forma generale (raccogliamo tutte le lettere e i numeri diversi dallo zero sul lato sinistro e lasciamo lo zero sul lato destro):

Componiamo l'equazione normale:

Esempio 3. Scrivi un'equazione tangente e un'equazione normale al grafico della funzione se l'ascissa è il punto tangente.

Soluzione. Troviamo l'ordinata del punto tangente:

Troviamo la derivata della funzione:

.

Troviamo il valore della derivata nel punto di tangenza, cioè la pendenza della tangente:

.

Troviamo l'equazione della tangente:

Prima di portare l'equazione alla sua forma generale, è necessario “pettinarla” un po': moltiplicare termine per termine per 4. Facciamo questo e riportiamo l'equazione alla sua forma generale:

Componiamo l'equazione normale:

Esempio 4. Scrivi un'equazione tangente e un'equazione normale al grafico della funzione se l'ascissa è il punto tangente.

Soluzione. Troviamo l'ordinata del punto tangente:

.

Troviamo la derivata della funzione:

Troviamo il valore della derivata nel punto di tangenza, cioè la pendenza della tangente:

.

Otteniamo l'equazione della tangente:

Portiamo l’equazione alla sua forma generale:

Componiamo l'equazione normale:

Un errore comune quando si scrivono equazioni tangenti e normali è non notare che la funzione fornita nell'esempio è complessa e calcolarne la derivata come derivata di una funzione semplice. I seguenti esempi provengono già da funzioni complesse(la lezione corrispondente si aprirà in una nuova finestra).

Esempio 5. Scrivi un'equazione tangente e un'equazione normale al grafico della funzione se l'ascissa è il punto tangente.

Soluzione. Troviamo l'ordinata del punto tangente:

Attenzione! Questa funzione è complessa, poiché l'argomento tangente (2 X) è esso stesso una funzione. Pertanto, troviamo la derivata di una funzione come derivata di una funzione complessa.

Y = f(x) e se a questo punto al grafico della funzione si può tracciare una tangente non perpendicolare all'asse delle ascisse, allora il coefficiente angolare della tangente è pari a f"(a). Abbiamo già lo ha utilizzato più volte Ad esempio, nel § 33 è stato stabilito che il grafico della funzione y = sin x (sinusoide) forma nell'origine un angolo di 45° con l'asse x (più precisamente, la tangente all'asse x). grafico che all'origine forma un angolo di 45° con la direzione positiva dell'asse x), e nell'esempio 5 § sono stati trovati 33 punti nella tabella data funzioni, in cui la tangente è parallela all'asse x. Nell'esempio 2 del § 33 è stata redatta un'equazione per la tangente al grafico della funzione y = x 2 nel punto x = 1 (più precisamente nel punto (1; 1), ma più spesso è solo il valore dell'ascissa indicato, ritenendo che, noto il valore dell'ascissa, allora si possa ricavare il valore dell'ordinata dall'equazione y = f(x)). In questa sezione svilupperemo un algoritmo per comporre un'equazione tangente al grafico di qualsiasi funzione.

Sia data la funzione y = f(x) e il punto M (a; f(a)), e sia noto anche che esiste f"(a). Creiamo un'equazione per la tangente al grafico data funzione in un dato punto. Questa equazione, come l'equazione di qualsiasi retta che non sia parallela all'asse delle ordinate, ha la forma y = kx+m, quindi il compito è trovare i valori dei coefficienti k e m.

Non ci sono problemi con il coefficiente angolare k: sappiamo che k = f"(a). Per calcolare il valore di m utilizziamo il fatto che la retta desiderata passa per il punto M(a; f(a)) Ciò significa che se sostituiamo il punto di coordinate M nell'equazione della retta, otteniamo l'uguaglianza corretta: f(a) = ka+m, da cui risulta che m = f(a) - ka.
Resta da sostituire i valori trovati dei coefficienti del kit in l'equazione Dritto:

Abbiamo ottenuto l'equazione per la tangente al grafico della funzione y = f(x) nel punto x=a.
Se, diciamo,
Sostituendo i valori trovati a = 1, f(a) = 1 f"(a) = 2 nell'equazione (1), otteniamo: y = 1+2(x-f), cioè y = 2x-1.
Confrontate questo risultato con quello ottenuto nell'esempio 2 del § 33. Naturalmente è accaduta la stessa cosa.
Creiamo un'equazione per la tangente al grafico della funzione y = tan x nell'origine. Abbiamo: questo significa cos x f"(0) = 1. Sostituendo i valori trovati a = 0, f(a) = 0, f"(a) = 1 nell'equazione (1), otteniamo: y = x.
Per questo motivo nel § 15 (vedi Fig. 62) abbiamo tracciato la tangente attraverso l'origine delle coordinate con un angolo di 45° rispetto all'asse delle ascisse.
Risolverli abbastanza semplici esempi, in realtà abbiamo utilizzato un certo algoritmo, contenuto nella formula (1). Rendiamo esplicito questo algoritmo.

ALGORITMO PER LO SVILUPPO DI UN'EQUAZIONE TANGENTE AL GRAFICO DELLA FUNZIONE y = f(x)

1) Designare l'ascissa del punto di tangenza con la lettera a.
2) Calcolare 1 (a).
3) Trova f"(x) e calcola f"(a).
4) Sostituisci i numeri trovati a, f(a), (a) nella formula (1).

Esempio 1. Scrivi un'equazione per la tangente al grafico della funzione nel punto x = 1.
Usiamo l'algoritmo, tenendo conto di quello in in questo esempio

Nella fig. 126 viene rappresentata un'iperbole, viene costruita una retta y = 2.
Il disegno conferma i calcoli precedenti: infatti la retta y = 2 tocca l'iperbole nel punto (1; 1).

Risposta: y = 2-x.
Esempio 2. Disegna una tangente al grafico della funzione in modo che sia parallela alla retta y = 4x - 5.
Chiariamo la formulazione del problema. Il requisito di "disegnare una tangente" di solito significa "formare un'equazione per la tangente". Questo è logico, perché se una persona fosse in grado di creare un'equazione per una tangente, difficilmente avrà difficoltà a costruire una linea retta sul piano delle coordinate utilizzando la sua equazione.
Usiamo l'algoritmo per comporre l'equazione della tangente, tenendo conto che in questo esempio però, a differenza dell'esempio precedente, c'è ambiguità: l'ascissa del punto tangente non è esplicitamente indicata.
Cominciamo a pensare in questo modo. La tangente desiderata deve essere parallela alla retta y = 4x-5. Due rette sono parallele se e solo se le loro pendenze sono uguali. Ciò significa che il coefficiente angolare della tangente deve essere uguale al coefficiente angolare della retta data: Pertanto, possiamo trovare il valore di a dall'equazione f"(a) = 4.
Abbiamo:
Dall'equazione Ciò significa che ci sono due tangenti che soddisfano le condizioni del problema: una nel punto con ascissa 2, l'altra nel punto con ascissa -2.
Ora puoi seguire l'algoritmo.

Esempio 3. Dal punto (0; 1) traccia una tangente al grafico della funzione
Usiamo l'algoritmo per comporre l'equazione della tangente, tenendo conto che in questo esempio, si noti che qui, come nell'esempio 2, l'ascissa del punto tangente non è esplicitamente indicata. Tuttavia, seguiamo l'algoritmo.

Per condizione, la tangente passa per il punto (0; 1). Sostituendo i valori x = 0, y = 1 nell'equazione (2), otteniamo:
Come puoi vedere, in questo esempio, solo al quarto passo dell'algoritmo siamo riusciti a trovare l'ascissa del punto tangente. Sostituendo il valore a =4 nell'equazione (2), otteniamo:

Nella fig. 127 presenta un'illustrazione geometrica dell'esempio considerato: viene tracciato un grafico della funzione

Nel § 32 abbiamo notato che per una funzione y = f(x) avente derivata nel punto fisso x vale l'uguaglianza approssimata:

Per comodità di ulteriore ragionamento, cambiamo la notazione: invece di x scriveremo a, invece di scriveremo x e, di conseguenza, invece di scriveremo x-a. Allora l’uguaglianza approssimativa scritta sopra assumerà la forma:

Ora guarda la fig. 128. Si traccia una tangente al grafico della funzione y = f(x) nel punto M (a; f (a)). Il punto x è segnato sull'asse x vicino ad a. È chiaro che f(x) è l'ordinata del grafico della funzione in punto specificato X. Cos'è f(a) + f"(a) (x-a)? Questa è l'ordinata della tangente corrispondente allo stesso punto x - vedere la formula (1). Qual è il significato dell'uguaglianza approssimativa (3)? Il fatto che Per calcolare il valore approssimativo della funzione, prendi il valore dell'ordinata della tangente.

Esempio 4. Trova il valore approssimativo espressione numerica 1,02 7 .
Riguarda su come trovare il valore della funzione y = x 7 nel punto x = 1,02. Usiamo la formula (3), tenendo conto di ciò in questo esempio
Di conseguenza otteniamo:

Se usiamo una calcolatrice, otteniamo: 1,02 7 = 1,148685667...
Come puoi vedere, la precisione di approssimazione è abbastanza accettabile.
Risposta: 1,02 7 =1,14.

A.G. Mordkovich Algebra 10a elementare

Pianificazione tematica del calendario in matematica, video in matematica online, download di Matematica a scuola

Contenuto della lezione appunti di lezione metodi di accelerazione della presentazione delle lezioni con frame di supporto tecnologie interattive Pratica compiti ed esercizi autotest workshop, corsi di formazione, casi, ricerche compiti a casa domande di discussione domande retoriche degli studenti Illustrazioni audio, video clip e contenuti multimediali fotografie, immagini, grafica, tabelle, diagrammi, umorismo, aneddoti, barzellette, fumetti, parabole, detti, cruciverba, citazioni Componenti aggiuntivi abstract articoli trucchi per i curiosi presepi libri di testo dizionario base e aggiuntivo dei termini altro Miglioramento di libri di testo e lezionicorreggere gli errori nel libro di testo aggiornamento di un frammento in un libro di testo, elementi di innovazione nella lezione, sostituzione di conoscenze obsolete con nuove Solo per insegnanti lezioni perfette piano di calendario per l'anno linee guida programmi di discussione Lezioni integrate