Multiplikasjon. Multiplisere og dele rasjonelle tall

) og nevner for nevner (vi får nevneren til produktet).

Formel for å multiplisere brøker:

For eksempel:

Før du begynner å multiplisere tellere og nevnere, må du sjekke om brøken kan reduseres. Hvis du kan redusere brøken, vil det være lettere for deg å gjøre ytterligere beregninger.

Å dele en vanlig brøk med en brøk.

Å dele brøker som involverer naturlige tall.

Det er ikke så skummelt som det virker. Som ved addisjon konverterer vi heltallet til en brøk med én i nevneren. For eksempel:

Multiplisere blandede fraksjoner.

Regler for å multiplisere brøker (blandet):

konvertere blandede fraksjoner til uekte fraksjoner;
multiplisere tellerne og nevnerne av brøker;
reduser fraksjonen;
Hvis du får en uekte brøk, så konverterer vi uekte brøk til en blandet brøk.

Merk!Å multiplisere blandet fraksjon til en annen blandet brøk, må du først konvertere dem til form av uekte brøker, og deretter multiplisere i henhold til multiplikasjonsregelen vanlige brøker.

Den andre måten å multiplisere en brøk med et naturlig tall.

Det kan være mer praktisk å bruke den andre metoden for å multiplisere en vanlig brøk med et tall.

Merk! For å multiplisere en brøk med et naturlig tall, må du dele nevneren til brøken på dette tallet og la telleren være uendret.

Fra eksemplet gitt ovenfor er det klart at dette alternativet er mer praktisk å bruke når nevneren til en brøk deles uten en rest med et naturlig tall.

Fleretasjes brøker.

På videregående støter man ofte på tre-etasjers (eller flere) brøker. Eksempel:

For å bringe en slik brøk til sin vanlige form, bruk divisjon gjennom 2 poeng:

Merk! Ved deling av brøker er rekkefølgen på delingen svært viktig. Vær forsiktig, det er lett å bli forvirret her.

Merk, For eksempel:

Når du deler en på en hvilken som helst brøk, vil resultatet være den samme brøken, bare invertert:

Praktiske tips for å multiplisere og dele brøker:

1. Det viktigste når du arbeider med brøkuttrykk er nøyaktighet og oppmerksomhet. Gjør alle beregninger nøye og nøyaktig, konsentrert og tydelig. Det er bedre å skrive noen ekstra linjer i utkastet enn å gå seg vill i hodeberegninger.

2. I oppgaver med forskjellige typer brøker - gå til formen for vanlige brøker.

3. Vi reduserer alle brøker til det ikke lenger er mulig å redusere.

4. Fleretasjes brøkuttrykk vi bringer dem inn i vanlig form ved å bruke divisjon gjennom 2 poeng.

5. Del en enhet med en brøk i hodet, bare snu brøken.

I denne artikkelen skal vi ta for oss multiplisere tall med forskjellige fortegn. Her skal vi først formulere regelen for å multiplisere positive og negative tall, begrunne den og deretter vurdere bruken av denne regelen når vi løser eksempler.

Sidenavigering.

Regel for å multiplisere tall med forskjellige fortegn

Å multiplisere et positivt tall med et negativt tall, så vel som et negativt tall med et positivt tall, utføres som følger: regelen for å multiplisere tall med forskjellige tegn : for å multiplisere tall med forskjellige tegn, må du multiplisere og sette et minustegn foran det resulterende produktet.

La oss skrive det ned denne regelen i brevform. For ethvert positivt reelt tall a og ethvert negativt reelt tall −b, er likheten a·(−b)=−(|a|·|b|) , og også for et negativt tall −a og et positivt tall b er likheten (−a)·b=−(|a|·|b|) .

Regelen for å multiplisere tall med forskjellige fortegn er helt i tråd med egenskaper ved operasjoner med reelle tall. På grunnlag av dem er det faktisk lett å vise at for reelle og positive tall a og b en kjede av likheter i formen a·(−b)+a·b=a·((−b)+b)=a·0=0, som beviser at a·(−b) og a·b er motsatte tall, noe som innebærer likheten a·(−b)=−(a·b) . Og av den følger gyldigheten av den aktuelle multiplikasjonsregelen.

Det skal bemerkes at den oppgitte regelen for multiplikasjon av tall med forskjellige fortegn er gyldig for både reelle tall og rasjonelle tall og for heltall. Dette følger av at operasjoner med rasjonelle tall og heltall har de samme egenskapene som ble brukt i beviset ovenfor.

Det er klart at å multiplisere tall med forskjellige fortegn i henhold til den resulterende regelen kommer ned til å multiplisere positive tall.

Det gjenstår bare å vurdere eksempler på bruken av den demonterte multiplikasjonsregelen når du multipliserer tall med forskjellige fortegn.

Eksempler på å multiplisere tall med forskjellige fortegn

La oss se på flere løsninger eksempler på å multiplisere tall med forskjellige fortegn. La oss starte med en enkel sak for å fokusere på trinnene i regelen i stedet for beregningskompleksiteten.

Multipliser det negative tallet −4 med det positive tallet 5.

I henhold til regelen for å multiplisere tall med forskjellige tegn, må vi først multiplisere de absolutte verdiene til de opprinnelige faktorene. Modul −4 er lik 4, og modul 5 er lik 5, og multiplikasjon naturlige tall 4 og 5 gir 20. Til slutt gjenstår det å sette et minustegn foran det resulterende tallet, vi har −20. Dette fullfører multiplikasjonen.

Kort fortalt kan løsningen skrives som følger: (−4)·5=−(4·5)=−20.

(−4)·5=−20.

Når du multipliserer brøker med forskjellige fortegn, må du kunne multiplisere vanlige brøker, multiplisere desimaler og deres kombinasjoner med naturlige og blandede tall.

Multipliser tall med forskjellige fortegn 0, (2) og.

Etter å ha utført konverteringen av en periodisk desimalbrøk til en vanlig brøk, og også etter å ha utført overgangen fra et blandet tall til en uekte brøk, fra det opprinnelige produktet kommer vi til produktet av vanlige brøker med forskjellige tegn på formen . Dette produktet er lik regelen for å multiplisere tall med forskjellige fortegn. Det gjenstår bare å multiplisere de vanlige brøkene i parentes, vi har .

Separat er det verdt å nevne multiplikasjonen av tall med forskjellige fortegn, når en eller begge faktorer er

La oss nå forholde oss til multiplikasjon og divisjon.

La oss si at vi må multiplisere +3 med -4. Hvordan gjøre det?

La oss vurdere en slik sak. Tre personer er i gjeld og har $4 i gjeld hver. Hva er den totale gjelden? For å finne den må du legge sammen alle tre gjeldene: 4 dollar + 4 dollar + 4 dollar = 12 dollar. Vi bestemte at tillegg av tre tall 4 er betegnet som 3x4. Siden vi i dette tilfellet snakker om gjeld, er det et "-"-tegn før 4. Vi vet at den totale gjelden er $12, så problemet vårt blir nå 3x(-4)=-12.

Vi vil få det samme resultatet hvis, i henhold til problemet, hver av de fire personene har en gjeld på $3. Med andre ord, (+4)x(-3)=-12. Og siden rekkefølgen på faktorene ikke spiller noen rolle, får vi (-4)x(+3)=-12 og (+4)x(-3)=-12.

La oss oppsummere resultatene. Når du multipliserer ett positivt tall og ett negativt tall, vil resultatet alltid være et negativt tall. Den numeriske verdien av svaret vil være den samme som ved positive tall. Produkt (+4)x(+3)=+12. Tilstedeværelsen av "-"-tegnet påvirker bare tegnet, men påvirker ikke den numeriske verdien.

Hvordan multiplisere to negative tall?

Dessverre er det veldig vanskelig å komme opp med et passende eksempel fra det virkelige liv om dette emnet. Det er lett å forestille seg en gjeld på 3 eller 4 dollar, men det er absolutt umulig å forestille seg -4 eller -3 personer som har satt seg i gjeld.

Kanskje vi går en annen vei. I multiplikasjon, når tegnet til en av faktorene endres, endres fortegnet til produktet. Hvis vi endrer tegnene til begge faktorene, må vi endre to ganger arbeidsmerke, først fra positivt til negativt, og deretter omvendt, fra negativt til positivt, det vil si at produktet vil ha et innledende tegn.

Derfor er det ganske logisk, selv om det er litt merkelig, at (-3) x (-4) = +12.

Skiltposisjon når multiplisert endres det slik:

positivt tall x positivt tall = positivt tall;
negativt tall x positivt tall = negativt tall;
positivt tall x negativt tall = negativt tall;
negativt tall x negativt tall = positivt tall.

Med andre ord, multipliserer to tall med samme fortegn, får vi et positivt tall. Multipliserer to tall med forskjellige fortegn, får vi et negativt tall.

Den samme regelen gjelder for handlingen motsatt av multiplikasjon - for.

Du kan enkelt verifisere dette ved å kjøre inverse multiplikasjonsoperasjoner. I hvert av eksemplene ovenfor, hvis du multipliserer kvotienten med divisor, vil du få utbyttet og sørge for at den har samme fortegn, for eksempel (-3)x(-4)=(+12).

Siden vinteren kommer, er det på tide å tenke på hva du skal bytte jernhestens sko til for ikke å skli på isen og føle deg trygg på vinterveiene. Du kan for eksempel kjøpe Yokohama-dekk på nettstedet: mvo.ru eller noen andre, det viktigste er at de er av høy kvalitet, mer informasjon og priser kan du finne ut på nettstedet Mvo.ru.

Denne artikkelen gir en detaljert oversikt dele tall med forskjellige fortegn. Først er regelen for å dele tall med forskjellige fortegn gitt. Nedenfor er eksempler på å dele positive tall med negative og negative tall med positive.

Sidenavigering.

Regel for å dele tall med forskjellige fortegn

I artikkelinndelingen av heltall fikk man en regel for å dele heltall med forskjellige fortegn. Det kan utvides til både rasjonelle tall og reelle tall ved å gjenta alle resonnementene fra artikkelen ovenfor.

Så, regel for å dele tall med forskjellige fortegn har følgende formulering: for å dele et positivt tall på et negativt eller et negativt tall med et positivt, må du dele utbyttet på divisormodulen, og sette et minustegn foran det resulterende tallet.

La oss skrive denne delingsregelen med bokstaver. Hvis tallene a og b har forskjellige fortegn, er formelen gyldig a:b=−|a|:|b| .

Fra den oppgitte regelen er det klart at resultatet av å dele tall med forskjellige fortegn er et negativt tall. Faktisk, siden modulen til utbyttet og modulen til divisoren er positive tall, er kvotienten deres et positivt tall, og minustegnet gjør dette tallet negativt.

Legg merke til at regelen som vurderes reduserer delingen av tall med forskjellige fortegn til delingen av positive tall.

Du kan gi en annen formulering av regelen for å dele tall med forskjellige fortegn: for å dele tallet a med tallet b, må du multiplisere tallet a med tallet b −1, det inverse av tallet b. Det er, a:b=a b −1 .

Denne regelen kan brukes når det er mulig å gå utover settet med heltall (siden ikke hvert heltall har en invers). Med andre ord gjelder det settet med rasjonelle tall så vel som settet med reelle tall.

Det er klart at denne regelen for å dele tall med forskjellige fortegn lar deg gå fra divisjon til multiplikasjon.

Den samme regelen brukes når du deler negative tall.

Det gjenstår å vurdere hvordan denne regelen for å dele tall med forskjellige tegn brukes når du løser eksempler.

Eksempler på å dele tall med forskjellige fortegn

La oss vurdere løsninger på flere egenskaper eksempler på å dele tall med forskjellige fortegnå forstå prinsippet om å anvende reglene fra forrige avsnitt.

Del det negative tallet −35 med det positive tallet 7.

Regelen for å dele tall med forskjellige fortegn foreskriver først å finne modulene til utbytte og divisor. Modulen til −35 er 35, og modulen til 7 er 7. Nå må vi dele utbyttemodulen med divisormodulen, det vil si at vi må dele 35 med 7. Når vi husker hvordan deling av naturlige tall utføres, får vi 35:7=5. Det siste trinnet som gjenstår i regelen for å dele tall med forskjellige fortegn er å sette et minus foran det resulterende tallet, vi har −5.

Her er hele løsningen: .

Det var mulig å gå ut fra en annen formulering av regelen for å dele tall med forskjellige fortegn. I dette tilfellet finner vi først inversen av divisor 7. Dette tallet er den vanlige brøken 1/7. Dermed, . Det gjenstår å multiplisere tall med forskjellige tegn: . Selvfølgelig kom vi til samme resultat.

(−35):7=−5 .

Regn ut kvotienten 8:(−60) .

I følge regelen for å dele tall med forskjellige fortegn har vi 8:(−60)=−(|8|:|−60|)=−(8:60) . Det resulterende uttrykket tilsvarer en negativ ordinær brøk (se divisjonstegnet som en brøklinje), du kan redusere brøken med 4, vi får .

La oss skrive ned hele løsningen kort: .

Når du deler rasjonelle brøktall med forskjellige fortegn, blir deres utbytte og divisor vanligvis representert som vanlige brøker. Dette skyldes det faktum at det ikke alltid er praktisk å utføre divisjon med tall i annen notasjon (for eksempel i desimal).

Modulen til utbyttet er lik, og modulen til divisoren er 0,(23) . For å dele modulen til utbyttet med modulen til divisoren, la oss gå videre til vanlige brøker.

I denne leksjonen Multiplikasjon og divisjon av rasjonelle tall vurderes.

Leksjonens innhold

Multiplisere rasjonelle tall

Reglene for å multiplisere heltall gjelder også for rasjonelle tall. Med andre ord, for å multiplisere rasjonelle tall, må du kunne

Du må også kjenne til de grunnleggende lovene for multiplikasjon, for eksempel: den kommutative loven for multiplikasjon, den assosiative loven for multiplikasjon, den distributive loven for multiplikasjon og multiplikasjon med null.

Eksempel 1. Finn verdien av et uttrykk

Dette er multiplikasjon av rasjonelle tall med forskjellige fortegn. For å multiplisere rasjonelle tall med forskjellige tegn, må du multiplisere modulene deres og sette et minus foran det resulterende svaret.

For å tydelig se at vi har å gjøre med tall som har forskjellige fortegn, legger vi hvert rasjonelt tall i parentes sammen med dets tegn

Modulen til tallet er lik , og modulen til tallet er lik . Etter å ha multiplisert de resulterende modulene som positive brøker, fikk vi svaret, men før svaret satte vi et minus, som regelen krevde av oss. For å sikre dette minus før svaret, ble multiplikasjonen av moduler utført i parentes, innledet med et minus.

Den korte løsningen ser slik ut:

Eksempel 2. Finn verdien av et uttrykk

Eksempel 3. Finn verdien av et uttrykk

Dette er multiplikasjonen av negative rasjonelle tall. For å multiplisere negative rasjonelle tall, må du multiplisere modulene deres og sette et pluss foran det resulterende svaret

Løsning for dette eksemplet kan skrives kort:

Eksempel 4. Finn verdien av et uttrykk

Løsningen for dette eksemplet kan skrives kort:

Eksempel 5. Finn verdien av et uttrykk

Dette er multiplikasjon av rasjonelle tall med forskjellige fortegn. La oss multiplisere modulene til disse tallene og sette et minus foran det resulterende svaret

Den korte løsningen vil se mye enklere ut:

Eksempel 6. Finn verdien av et uttrykk

La oss konvertere det blandede tallet til en uekte brøk. La oss omskrive resten som det er

Vi oppnådde multiplikasjon av rasjonelle tall med forskjellige fortegn. La oss multiplisere modulene til disse tallene og sette et minus foran det resulterende svaret. Oppføringen med moduler kan hoppes over for ikke å rote uttrykket

Løsningen for dette eksemplet kan skrives kort

Eksempel 7. Finn verdien av et uttrykk

Dette er multiplikasjon av rasjonelle tall med forskjellige fortegn. La oss multiplisere modulene til disse tallene og sette et minus foran det resulterende svaret

Først viste svaret seg å være en uekte brøk, men vi fremhevet hele delen i den. noter det hele delen ble separert fra fraksjonsmodulen. Det resulterende blandede tallet ble satt i parentes foran med et minustegn. Dette gjøres for å sikre at kravet i regelen oppfylles. Og regelen krevde at svaret mottatt ble innledet med et minus.

Løsningen for dette eksemplet kan skrives kort:

Eksempel 8. Finn verdien av et uttrykk

Først, la oss multiplisere og og multiplisere det resulterende tallet med det gjenværende tallet 5. Vi hopper over oppføringen med moduler for ikke å rote uttrykket.

Svar: uttrykksverdi er lik −2.

Eksempel 9. Finn betydningen av uttrykket:

La oss oversette blandede tall til uekte brøker:

Vi fikk multiplikasjonen av negative rasjonelle tall. La oss multiplisere modulene til disse tallene og sette et pluss foran det resulterende svaret. Oppføringen med moduler kan hoppes over for ikke å rote uttrykket

Eksempel 10. Finn verdien av et uttrykk

Uttrykket består av flere faktorer. I følge den assosiative loven om multiplikasjon, hvis et uttrykk består av flere faktorer, vil ikke produktet avhenge av rekkefølgen av handlinger. Dette lar oss vurdere et gitt uttrykk i hvilken som helst rekkefølge.

La oss ikke finne opp hjulet på nytt, men beregne dette uttrykket fra venstre til høyre i rekkefølgen av faktorene. La oss hoppe over oppføringen med moduler for ikke å rote uttrykket

Tredje handling:

Fjerde handling:

Svar: verdien av uttrykket er

Eksempel 11. Finn verdien av et uttrykk

La oss huske loven om multiplikasjon med null. Denne loven sier at et produkt er lik null hvis minst en av faktorene er lik null.

I vårt eksempel er en av faktorene lik null, så uten å kaste bort tid svarer vi at verdien av uttrykket er lik null:

Eksempel 12. Finn verdien av et uttrykk

Produktet er lik null hvis minst en av faktorene er lik null.

I vårt eksempel er en av faktorene lik null, så uten å kaste bort tid svarer vi at verdien av uttrykket er lik null:

Eksempel 13. Finn verdien av et uttrykk

Du kan bruke rekkefølgen på handlingene og først beregne uttrykket i parentes og multiplisere det resulterende svaret med en brøk.

Du kan også bruke den distributive loven om multiplikasjon - multipliser hvert ledd av summen med en brøk og legg til de resulterende resultatene. Vi vil bruke denne metoden.

I henhold til operasjonsrekkefølgen, hvis et uttrykk inneholder addisjon og multiplikasjon, må multiplikasjonen utføres først. Derfor, i det resulterende nye uttrykket, la oss sette i parentes de parametrene som må multipliseres. På denne måten kan vi tydelig se hvilke handlinger vi skal utføre tidligere og hvilke senere:

Tredje handling:

Svar: uttrykksverdi er lik

Løsningen for dette eksemplet kan skrives mye kortere. Det vil se slik ut:

Det er klart at dette eksemplet kan løses selv i ens sinn. Derfor bør du utvikle ferdighetene til å analysere et uttrykk før du løser det. Det er sannsynlig at det kan løses mentalt og spare mye tid og nerver. Og i prøver og eksamener er tid som du vet veldig verdifull.

Eksempel 14. Finn verdien av uttrykket −4,2 × 3,2

Dette er multiplikasjon av rasjonelle tall med forskjellige fortegn. La oss multiplisere modulene til disse tallene og sette et minus foran det resulterende svaret

Legg merke til hvordan modulene til rasjonelle tall ble multiplisert. I dette tilfellet, for å multiplisere modulene til rasjonelle tall, tok det .

Eksempel 15. Finn verdien av uttrykket −0,15 × 4

Dette er multiplikasjon av rasjonelle tall med forskjellige fortegn. La oss multiplisere modulene til disse tallene og sette et minus foran det resulterende svaret

Legg merke til hvordan modulene til rasjonelle tall ble multiplisert. I dette tilfellet, for å multiplisere modulene til rasjonelle tall, var det nødvendig å kunne.

Eksempel 16. Finn verdien av uttrykket −4,2 × (−7,5)

Dette er multiplikasjonen av negative rasjonelle tall. La oss multiplisere modulene til disse tallene og sette et pluss foran det resulterende svaret

Deling av rasjonelle tall

Reglene for å dele heltall gjelder også for rasjonelle tall. Med andre ord, for å kunne dele rasjonelle tall, må du kunne

Ellers brukes de samme metodene for å dele ordinære og desimalbrøker. For å dele en vanlig brøk med en annen brøk, må du multiplisere den første brøken med den resiproke av den andre brøken.

Og for å dele en desimalbrøk i en annen desimalbrøk, må du flytte desimaltegnet i utbyttet og i divisoren til høyre med så mange sifre som det er etter desimaltegnet i divisoren, og deretter utføre divisjonen som med en vanlig nummer.

Eksempel 1. Finn betydningen av uttrykket:

Dette er delingen av rasjonelle tall med forskjellige fortegn. For å beregne et slikt uttrykk, må du multiplisere den første brøken med den gjensidige av den andre.

Så la oss multiplisere den første brøken med den gjensidige av den andre.

Vi oppnådde multiplikasjon av rasjonelle tall med forskjellige fortegn. Og vi vet allerede hvordan vi beregner slike uttrykk. For å gjøre dette må du multiplisere modulene til disse rasjonelle tallene og sette et minus foran det resulterende svaret.

La oss fullføre dette eksemplet til slutten. Oppføringen med moduler kan hoppes over for ikke å rote uttrykket

Så verdien av uttrykket er

Den detaljerte løsningen er som følger:

En kort løsning vil se slik ut:

Eksempel 2. Finn verdien av et uttrykk

Dette er delingen av rasjonelle tall med forskjellige fortegn. For å beregne dette uttrykket, må du multiplisere den første brøken med den gjensidige av den andre.

Den resiproke av den andre brøken er brøken. La oss gange den første brøken med den:

En kort løsning vil se slik ut:

Eksempel 3. Finn verdien av et uttrykk

Dette er delingen av negative rasjonelle tall. For å beregne dette uttrykket må du igjen multiplisere den første brøken med den gjensidige av den andre.

Den resiproke av den andre brøken er brøken. La oss gange den første brøken med den:

Vi fikk multiplikasjonen av negative rasjonelle tall. Vi vet allerede hvordan et slikt uttrykk beregnes. Du må multiplisere modulene til rasjonelle tall og sette et pluss foran det resulterende svaret.

La oss fullføre dette eksemplet til slutten. Du kan hoppe over oppføringen med moduler for ikke å rote uttrykket:

Eksempel 4. Finn verdien av et uttrykk

For å beregne dette uttrykket må du multiplisere det første tallet −3 med den inverse brøken av .

Den gjensidige av en brøk er brøken. Multipliser det første tallet −3 med det

Eksempel 6. Finn verdien av et uttrykk

For å beregne dette uttrykket må du gange den første brøken med tallet gjensidig av antall 4.

Den gjensidige av tallet 4 er en brøk. Multipliser den første brøken med den

Eksempel 5. Finn verdien av et uttrykk

For å beregne dette uttrykket må du multiplisere den første brøken med inversen av −3

Inversen av −3 er en brøk. La oss gange den første brøken med den:

Eksempel 6. Finn verdien av uttrykket −14.4: 1.8

Dette er delingen av rasjonelle tall med forskjellige fortegn. For å beregne dette uttrykket må du dele utbyttemodulen med divisormodulen og sette et minus før det resulterende svaret.

Legg merke til hvordan modulen til utbytte ble delt med modulen til divisor. I dette tilfellet, for å gjøre det riktig, var det nødvendig å kunne.

Hvis du ikke vil rote med desimaler (og dette skjer ofte), så konverter disse blandede tallene til uekte brøker, og gjør så selve divisjonen.

La oss beregne det forrige uttrykket −14.4: 1.8 på denne måten. La oss konvertere desimaler til blandede tall:

La oss nå konvertere de resulterende blandede tallene til uekte brøker:

Nå kan du gjøre divisjon direkte, nemlig dele en brøk med en brøk. For å gjøre dette må du multiplisere den første brøken med den inverse brøkdelen av den andre:

Eksempel 7. Finn verdien av et uttrykk

La oss konvertere desimalbrøken −2,06 til en uekte brøk, og gange denne brøken med den resiproke av den andre brøken:

Fleretasjes brøker

Du kan ofte komme over et uttrykk der brøkdelingen er skrevet ved hjelp av en brøklinje. For eksempel kan uttrykket skrives som følger:

Hva er forskjellen mellom uttrykkene og ? Det er egentlig ingen forskjell. Disse to uttrykkene har samme betydning og et likhetstegn kan plasseres mellom dem:

I det første tilfellet er divisjonstegnet et kolon og uttrykket er skrevet på én linje. I det andre tilfellet skrives delingen av brøker ved hjelp av en brøklinje. Resultatet er en brøkdel som folk blir enige om å ringe flere etasjer.

Når du møter slike uttrykk med flere historier, må du bruke de samme reglene for å dele vanlige brøker. Den første brøken må multipliseres med den resiproke av den andre.

Det er ekstremt upraktisk å bruke slike brøker i en løsning, så du kan skrive dem på en forståelig form ved å bruke et kolon i stedet for en brøklinje som et delingstegn.

La oss for eksempel skrive en brøk med flere historier i en forståelig form. For å gjøre dette må du først finne ut hvor den første brøken er og hvor den andre er, fordi det ikke alltid er mulig å gjøre dette riktig. Flertasjes brøker har flere brøklinjer som kan være forvirrende. Hovedfraksjonslinjen, som skiller den første fraksjonen fra den andre, er vanligvis lengre enn resten.

Etter å ha bestemt hovedbrøklinjen, kan du enkelt forstå hvor den første brøken er og hvor den andre er:

Eksempel 2.

Vi finner hovedbrøklinjen (den er den lengste) og ser at heltallet −3 er delt med en fellesbrøk

Og hvis vi feilaktig tok den andre brøklinjen som hovedlinjen (den som er kortere), ville det vise seg at vi deler brøken med heltallet 5. I dette tilfellet, selv om dette uttrykket er riktig beregnet, problemet vil bli løst feil, siden utbyttet i dette I dette tilfellet er tallet −3, og divisor er brøken .

Eksempel 3. La oss skrive flernivåbrøken i en forståelig form

Vi finner hovedbrøklinjen (den er den lengste) og ser at brøken er delt på heltall 2

Og hvis vi feilaktig tok den første brøklinjen som den ledende (den som er kortere), så vil det vise seg at vi deler heltallet −5 med brøken, selv om dette uttrykket er riktig beregnet. problemet vil bli løst feil, siden utbyttet i dette tilfellet er brøken , og divisoren er heltall 2.

Til tross for at flernivåbrøker er upraktiske å jobbe med, vil vi møte dem veldig ofte, spesielt når vi studerer høyere matematikk.

Naturligvis tar det ekstra tid og plass å konvertere en brøk med flere etasjer til en forståelig form. Derfor kan du bruke mer rask metode. Denne metoden er praktisk, og utgangen lar deg få et ferdig uttrykk der den første brøken allerede er multiplisert med den gjensidige brøkdelen av den andre.

Denne metoden implementeres som følger:

Hvis brøken for eksempel er fire etasjer, heves tallet i første etasje til toppetasjen. Og figuren som ligger i andre etasje er hevet til tredje etasje. De resulterende tallene må forbindes med multiplikasjonstegn (×)

Som et resultat, utenom den mellomliggende notasjonen, får vi et nytt uttrykk der den første brøken allerede er multiplisert med den resiproke brøken av den andre. Bekvemmelighet og det er det!

For å unngå feil når du bruker denne metoden, kan du følge følgende regel:

Fra første til fjerde. Fra andre til tredje.

I regelen vi snakker om om gulvene. Figuren fra første etasje skal heves til fjerde etasje. Og figuren fra andre etasje må heves til tredje etasje.

La oss prøve å beregne en brøk med flere etasjer ved å bruke regelen ovenfor.

Så vi hever tallet som ligger i første etasje til fjerde etasje, og øker tallet som ligger i andre etasje til tredje etasje

Som et resultat, utenom den mellomliggende notasjonen, får vi et nytt uttrykk der den første brøken allerede er multiplisert med den resiproke brøken av den andre. Deretter kan du bruke din eksisterende kunnskap:

La oss prøve å beregne en brøk på flere nivåer ved å bruke et nytt skjema.

Det er kun første, andre og fjerde etasje. Det er ingen tredje etasje. Men vi avviker ikke fra grunnordningen: vi hever figuren fra første etasje til fjerde etasje. Og siden det ikke er noen tredje etasje, lar vi nummeret ligge i andre etasje som det er

Som et resultat, utenom den mellomliggende notasjonen, fikk vi et nytt uttrykk der det første tallet −3 allerede er multiplisert med den gjensidige brøken av det andre. Deretter kan du bruke din eksisterende kunnskap:

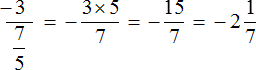
La oss prøve å beregne brøken med flere etasjer ved å bruke den nye ordningen.

Det er bare andre, tredje og fjerde etasje. Det er ingen første etasje. Siden det ikke er første etasje, er det ingenting å gå opp til fjerde etasje, men vi kan heve figuren fra andre etasje til tredje:

Som et resultat, utenom den mellomliggende notasjonen, fikk vi et nytt uttrykk der den første brøken allerede er multiplisert med inversen av divisor. Deretter kan du bruke din eksisterende kunnskap:

Bruke variabler

Hvis uttrykket er komplekst og det ser ut til at det vil forvirre deg i prosessen med å løse problemet, kan en del av uttrykket settes inn i en variabel og deretter jobbe med denne variabelen.

Matematikere gjør ofte dette. Et komplekst problem brytes ned i enklere deloppgaver og løses. Deretter samles de løste deloppgavene til én helhet. Dette kreativ prosess og dette er noe man lærer gjennom årene gjennom hard trening.

Bruk av variabler er berettiget når man arbeider med flernivåbrøker. For eksempel:

Finn verdien av et uttrykk

Så det er et brøkuttrykk i telleren og i nevneren som det er brøkuttrykk. Med andre ord står vi igjen overfor en fleretasjes brøk, som vi ikke liker så godt.

Uttrykket i telleren kan legges inn i en variabel med et hvilket som helst navn, for eksempel:

Men i matematikk, i et slikt tilfelle, er det vanlig å navngi variabler med store latinske bokstaver. La oss ikke bryte denne tradisjonen, og betegne det første uttrykket med en stor latinsk bokstav EN

Og uttrykket i nevneren kan betegnes med stor bokstav B

Nå tar vårt opprinnelige uttrykk formen. Det vil si at vi gjorde en erstatning numerisk uttrykk til en bokstav, etter å ha skrevet inn telleren og nevneren i variablene A og B.

Nå kan vi separat beregne verdiene til variabel A og verdien av variabel B. Vi vil sette inn de ferdige verdiene i uttrykket.

La oss finne verdien av variabelen EN

La oss finne verdien av variabelen B

La oss nå erstatte verdiene deres i hoveduttrykket i stedet for variablene A og B:

Vi har fått en brøk med flere etasjer der vi kan bruke skjemaet "fra første til fjerde, fra andre til tredje", det vil si heve tallet som ligger i første etasje til fjerde etasje, og heve nummer som ligger i andre etasje til tredje etasje. Ytterligere beregninger vil ikke være vanskelig:

Dermed er verdien av uttrykket −1.

Selvfølgelig har vi vurdert enkleste eksempelet, men målet vårt var å lære hvordan vi kan bruke variabler for å gjøre ting enklere for oss selv, for å minimere feil.

Merk også at løsningen for dette eksemplet kan skrives uten å bruke variabler. Det vil se ut som

Denne løsningen er raskere og kortere, og i dette tilfellet er det mer fornuftig å skrive det på denne måten, men hvis uttrykket viser seg å være komplekst, bestående av flere parametere, parenteser, røtter og potenser, så er det tilrådelig å beregne det i flere stadier, og legger inn deler av uttrykkene i variabler.

Likte du leksjonen?
Bli med i vår ny gruppe VKontakte og begynn å motta varsler om nye leksjoner

Leksjonens mål:

Pedagogisk:

formulere regler for å multiplisere tall med samme og forskjellige tegn;
mestre og forbedre ferdighetene til å multiplisere tall med forskjellige tegn.

Pedagogisk:

utvikling av mentale operasjoner: sammenligning, generalisering, analyse, analogi;
ferdighetsutvikling selvstendig arbeid;
utvide horisonten til studentene.

Pedagogisk:

fremme en journalføringskultur;
utdanning av ansvar, oppmerksomhet;
vekke interesse for faget.

Leksjonstype: lære nytt materiale.

Utstyr: datamaskin, multimediaprojektor, kort til spillet "Mathematical Combat", tester, kunnskapskort.

Plakater på veggene:

Kunnskap er den mest utmerkede av eiendeler. Alle streber etter det, men det kommer ikke av seg selv.
Al-Biruni
I alt vil jeg komme til selve essensen...
B. Pasternak

Timeplan

Organisatorisk øyeblikk (1 min).
Innledningsforedrag ved lærer (3 min).
Muntlig arbeid (10 min).
Presentasjon av stoffet (15 min).
Matematisk kjede (5 min).
Hjemmelekser(2 minutter).
Test (6 min).
Leksjonssammendrag (3 min).

I løpet av timene

I. Organisatorisk øyeblikk

elevenes beredskap for timen.

II. Lærerens åpningstale

Gutter, vi møtte dere i dag ikke forgjeves, men for fruktbart arbeid: å få kunnskap.

Siden universet har eksistert,
Det er ingen som ikke trenger kunnskap.
Uansett hvilket språk og alder vi velger,
Mennesket har alltid strebet etter kunnskap...
Rudaki

I klassen skal vi studere nytt materiale, konsolider det, jobb selvstendig, evaluer deg selv og kameratene dine. Alle har et kunnskapskort på skrivebordet, der timen vår er delt inn i etapper. Poengene du har tjent på ulike stadier du vil selv legge inn leksjonen på dette kortet. Og på slutten av leksjonen vil vi oppsummere. Plasser disse kortene på et synlig sted.

III. Muntlig arbeid (i form av spillet "Mathematical Combat")

Gutter, før vi begynner nytt emne, la oss gjenta det vi lærte tidligere. Alle har et ark med spillet "Mathematical Combat" på skrivebordet. De vertikale og horisontale kolonnene inneholder tallene som må legges til. Disse tallene er merket med prikker. Vi vil skrive svarene i de cellene på feltet der prikkene er.

Tre minutter å fullføre. Vi startet arbeidet.

Nå utvekslet vi arbeider med skrivebordsnaboen vår og sjekker dem med hverandre. Hvis du mener at svaret er feil, så kryss det forsiktig ut og skriv det riktige ved siden av. La oss sjekke.

La oss nå sjekke svarene med skjermen ( De riktige svarene projiseres på skjermen).

For riktig løst

5 oppgaver gis 5 poeng;
4 oppgaver – 4 poeng;
3 oppgaver – 3 poeng;
2 oppgaver – 2 poeng;
1 oppgave – 1 poeng.

Bra gjort. De legger alt til side. Gutter, la oss legge inn antall poeng scoret for "Matematisk kamp" i kunnskapskortene våre ( Vedlegg 1).

IV. Presentasjon av materialet

Åpne arbeidsbøkene. Skriv ned nummeret, flott jobbet.

Hvilke operasjoner på positive og negative tall kjenner du til?
Hvordan legge til to negative tall?
Hvordan legge til to tall med forskjellige fortegn?
Hvordan trekke fra tall med forskjellige fortegn?
Du bruker alltid ordet "modul". Hva er modulen til et tall? EN?

Dagens leksjonstema er også knyttet til driften av antall forskjellige tegn. Men det var skjult i et anagram, der du må bytte bokstaver og få et kjent ord. La oss prøve å finne ut av det.

ENOZHEUMNI

Vi skriver ned emnet for leksjonen: "Multiplikasjon."

Hensikten med leksjonen vår: å bli kjent med multiplikasjonen av positive og negative tall og formulere regler for å multiplisere tall med både samme og forskjellige fortegn.

All oppmerksomhet til styret. Før du er en tabell med problemer, løse som vi vil formulere reglene for å multiplisere positive og negative tall.

2*3 = 6°C;
–2*3 = –6°С;
–2*(–3) = 6°С;
2*(–3) = –6°С;

1. Lufttemperaturen stiger med 2°C hver time. Nå viser termometeret 0°C ( Vedlegg 2– Termometer) (lysbilde 1 på datamaskinen).

Hvor mye fikk du?(6 ° MED).
Noen vil skrive løsningen på tavlen, og vi er alle i notatbøker.
La oss se på termometeret, fikk vi riktig svar? (lysbilde 2 på datamaskinen).

2. Lufttemperaturen synker med 2°C hver time. Termometeret viser nå 0°C (lysbilde 3 på datamaskinen). Hvilken lufttemperatur vil termometeret vise etter 3 timer?

Hvor mye fikk du?(–6 ° MED).
Vi skriver ned den tilsvarende løsningen på tavlen og i notatbøker. Analogi med oppgave 1.
.(lysbilde 4 på datamaskinen).

3. Lufttemperaturen synker med 2°C hver time. Termometeret viser nå 0°C (lysbilde 5 på datamaskinen).

Hvor mye fikk du?(6 ° MED).
Vi skriver ned den tilsvarende løsningen på tavlen og i notatbøker. Analogi med oppgave 1 og 2.
La oss sammenligne resultatet med termometeravlesningen.(lysbilde 6 på datamaskinen).

4. Lufttemperaturen stiger med 2°C hver time. Termometeret viser nå 0°C (lysbilde 7 på datamaskinen). Hvilken lufttemperatur viste termometeret for 3 timer siden?

Hvor mye fikk du?(–6 ° MED).
Vi skriver ned den tilsvarende løsningen på tavlen og i notatbøker. Analogi med oppgave 1-3.
La oss sammenligne resultatet med termometeravlesningen.(lysbilde 8 på datamaskinen).

Se på resultatene dine. Når du multipliserte tall med samme fortegn (eksempel 1 og 3), hvilket tegn fikk du svaret? (positiv).

Fint. Men i eksempel 3 er begge faktorene negative, og svaret er positivt. Hvilket matematisk konsept lar deg gå fra negative tall til positive? (modul).

Oppmerksomhetsregel: For å multiplisere to tall med samme fortegn, må du multiplisere deres absolutte verdier og sette et plusstegn foran resultatet. (2 personer gjentar).

La oss gå tilbake til eksempel 3. Hva er modulene (–2) og (–3) lik? La oss multiplisere disse modulene. Hvor mye fikk du? Med hvilket skilt?

Når du multipliserte tall med forskjellige fortegn (eksempel 2 og 4), hvilket tegn fikk du svaret? (negativ).

Formuler din egen regel for å multiplisere tall med forskjellige fortegn.

Regel: Når du multipliserer tall med forskjellige fortegn, må du multiplisere modulene deres og sette et minustegn foran resultatet. (2 personer gjentar).

La oss gå tilbake til eksempel nr. 2 og nr. 4. Hva er størrelsen på faktorene deres? La oss multiplisere disse modulene. Hvor mye fikk du? Hvilket tegn bør gis som et resultat?

Ved å bruke disse to reglene kan du også multiplisere brøker: desimal, blandet, ordinær.

Det er flere eksempler på tavlen foran deg. Vi bestemmer tre sammen med meg, og resten på egenhånd. Vær oppmerksom på opptaket og designet.

Bra gjort. La oss åpne lærebøkene og markere reglene som må læres til neste leksjon (side 190, §7 (punkt 35)). Å kjenne disse reglene vil hjelpe deg raskt å mestre delingen av positive og negative tall i fremtiden.

V. Matematisk kjede

Og nå vil Dunno sjekke hvordan du har lært det nye materialet og vil stille deg noen spørsmål. Vi må skrive ned løsningen og svarene i notatbøker ( Vedlegg 3– Matematisk kjede).

Datamaskin presentasjon
Hei folkens. Jeg ser at du er veldig smart og nysgjerrig, så jeg vil stille deg noen spørsmål. Vær forsiktig, spesielt med skilt.
Mitt første spørsmål er: multipliser (–3) med (–13).
Andre spørsmål: gang det du fikk i den første oppgaven med (–0,1).
Tredje spørsmål: multipliser resultatet av den andre oppgaven med (–2).
Fjerde spørsmål: gang (-1/3) med resultatet av den tredje oppgaven.
Og det siste, femte spørsmålet: beregn frysepunktet til kvikksølv ved å multiplisere resultatet av den fjerde oppgaven med 15.
Takk for arbeidet. Jeg ønsker deg suksess.

Gutter, la oss sjekke hvordan vi fullførte oppgavene. Alle reiste seg.

Hvor mye fikk du på den første oppgaven?

De som har et annet svar, setter seg ned, og de som setter seg ned gir vi oss selv 0 poeng for den matematiske kjeden på kunnskapsrekordkortet. Resten legger ikke noe.

Hvor mye fikk du i den andre oppgaven?

Hvis du har et annet svar, sett deg ned og legg til 1 poeng på kunnskapskortet ditt for den matematiske kjeden.

Hvor mye fikk du i den tredje oppgaven?

Hvis du har et annet svar, sett deg ned og legg til 2 poeng på kunnskapskortet ditt for den matematiske kjeden.

Hvor mye fikk du i den fjerde oppgaven?

For de som har et annet svar, sett deg ned og legg til 3 poeng på kunnskapskortet ditt for den matematiske kjeden.

Hvor mye fikk du i den femte oppgaven?

Hvis du har et annet svar, sett deg ned og legg til 4 poeng på kunnskapskortet ditt for den matematiske kjeden. De resterende gutta løste alle 5 oppgavene riktig. Sett deg ned, du gir deg selv 5 poeng for den matematiske kjeden på kunnskapskortet ditt.

Hva er frysepunktet for kvikksølv?(–39 °C).

VI. Hjemmelekser

§7 (punkt 35, side 190), nr. 1121 – lærebok: Matematikk. 6. klasse: [N.Ya.Vilenkin og andre]

Kreativ oppgave: Skriv en oppgave om å multiplisere positive og negative tall.

VII. Test

La oss gå videre til neste trinn i leksjonen: å utføre testen ( Vedlegg 4).

Du må løse oppgavene og sette ring rundt tallet på det riktige svaret. For de to første riktig utførte oppgavene får du 1 poeng, for 3. oppgave - 2 poeng, for 4. oppgave - 3 poeng. Vi startet arbeidet.

Δ –1 poeng;
o –2 poeng;
–3 poeng.

La oss nå skrive ned tallene på de riktige svarene i tabellen under testen. La oss sjekke resultatene. Du bør få tallet 1418 i de tomme cellene (jeg skriver på tavlen). Den som mottok det setter 7 poeng på kunnskapskortet. De som gjorde feil setter antall poeng kun for riktig utførte oppgaver på kunnskapskortet.

Den store krigen varte i nøyaktig 1418 dager. Patriotisk krig, en seier der det russiske folket kom til en høy pris. Og 9. mai 2010 feirer vi 65-årsjubileet for seieren over Nazi-Tyskland.