Ligning for tangenten til grafen for en funktion

P. Romanov, T. Romanova,
Magnitogorsk,
Chelyabinsk-regionen

Ligning for tangenten til grafen for en funktion

Artiklen blev publiceret med støtte fra ITAKA+ Hotel Complex. Når du bor i skibsbyggernes by Severodvinsk, vil du ikke støde på problemet med at finde midlertidig bolig. , Online hotelkompleks“ITHAKA+” http://itakaplus.ru, du kan nemt og hurtigt leje en lejlighed i byen, for enhver periode, med en daglig betaling.

På moderne scene udvikling af uddannelse, en af ​​dens hovedopgaver er dannelsen af ​​en kreativt tænkende personlighed. Evnen til kreativitet hos eleverne kan kun udvikles, hvis de systematisk er involveret i det grundlæggende i forskningsaktiviteter. Grundlaget for, at eleverne kan bruge deres kreative kræfter, evner og talenter, er dannet fuldgyldig viden og færdigheder. I denne henseende er problemet med at danne et system med grundlæggende viden og færdigheder for hvert emne i skolens matematikkursus af ikke ringe betydning. Samtidig bør fuldgyldige færdigheder ikke være det didaktiske mål for individuelle opgaver, men for et nøje gennemtænkt system af dem. I bredeste forstand forstås et system som et sæt af indbyrdes forbundne interagerende elementer med integritet og en stabil struktur.

Lad os overveje en teknik til at lære eleverne at skrive en ligning for en tangent til grafen for en funktion. I det væsentlige kommer alle problemer med at finde tangentligningen ned på behovet for at vælge fra et sæt (bundt, familie) af linjer dem, der opfylder et bestemt krav - de tangerer grafen for en bestemt funktion. I dette tilfælde kan det sæt af linjer, hvorfra valget udføres, specificeres på to måder:

a) et punkt, der ligger på xOy-planet (central blyant af linjer);
b) vinkelkoefficient (parallel stråle af rette linjer).

I denne henseende, når vi studerede emnet "Tangent til grafen for en funktion" for at isolere elementerne i systemet, identificerede vi to typer problemer:

1) problemer på en tangent givet af det punkt, den passerer igennem;
2) problemer på en tangent givet ved dens hældning.

Træning i at løse tangentproblemer blev udført ved hjælp af algoritmen foreslået af A.G. Mordkovich. Hans grundlæggende forskel fra de allerede kendte er, at tangenspunktets abscisse er angivet med bogstavet a (i stedet for x0), og derfor har tangentens ligning formen

y = f(a) + f "(a)(x – a)

(sammenlign med y = f(x 0) + f "(x 0)(x – x 0)). Dette metodisk teknik, efter vores mening, giver eleverne mulighed for hurtigt og nemt at forstå, hvor i den generelle tangentligning koordinaterne for det aktuelle punkt er skrevet, og hvor tangentpunkterne er.

Algoritme til at sammensætte tangentligningen til grafen for funktionen y = f(x)

1. Angiv abscissen af ​​tangentpunktet med bogstavet a.
2. Find f(a).
3. Find f "(x) og f "(a).
4. Erstat de fundne tal a, f(a), f "(a) i generel ligning tangent y = f(a) = f "(a)(x – a).

Denne algoritme kan kompileres på grundlag af elevernes uafhængige identifikation af operationer og rækkefølgen af ​​deres implementering.

Praksis har vist, at den sekventielle løsning af hvert af nøgleproblemerne ved hjælp af en algoritme giver dig mulighed for at udvikle færdighederne til at skrive ligningen for en tangent til grafen for en funktion i etaper, og trinene i algoritmen tjener som referencepunkter for handlinger . Denne tilgang svarer til teorien om den gradvise dannelse af mentale handlinger udviklet af P.Ya. Galperin og N.F. Talyzina.

I den første type opgaver blev to nøgleopgaver identificeret:

• tangenten passerer gennem et punkt, der ligger på kurven (opgave 1);
• tangenten går gennem et punkt, der ikke ligger på kurven (opgave 2).

Opgave 1. Skriv en ligning for tangenten til funktionens graf ved punkt M(3; – 2).

Løsning. Punkt M(3; – 2) er et tangentpunkt, da

1. a = 3 – abscisse af tangentpunktet.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – tangentligning.

Opgave 2. Skriv ligningerne for alle tangenter til grafen for funktionen y = – x 2 – 4x + 2, der går gennem punktet M(– 3; 6).

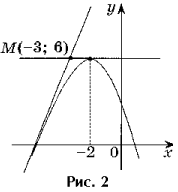Løsning. Punkt M(– 3; 6) er ikke et tangentpunkt, da f(– 3) 6 (fig. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – tangentligning.

Tangenten passerer gennem punktet M(– 3; 6), derfor opfylder dens koordinater tangentligningen.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.

Hvis a = – 4, så er tangentligningen y = 4x + 18.

Hvis a = – 2, så har tangentligningen formen y = 6.

I den anden type vil nøgleopgaverne være følgende:

• tangenten er parallel med en linje (opgave 3);
• tangenten passerer i en bestemt vinkel til den givne linje (opgave 4).

Opgave 3. Skriv ligningerne for alle tangenter til grafen for funktionen y = x 3 – 3x 2 + 3, parallelt med linjen y = 9x + 1.

Løsning.

1. a – abscisse af tangentpunktet.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Men på den anden side er f "(a) = 9 (parallelismebetingelse). Det betyder, at vi skal løse ligningen 3a 2 – 6a = 9. Dens rødder er a = – 1, a = 3 (fig. 3) ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9 (x + 1);

y = 9x + 8 – tangentligning;

1) a = 3;
2) f(3) = 3;
3) f"(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – tangentligning.

Opgave 4. Skriv tangentens ligning til grafen for funktionen y = 0,5x 2 – 3x + 1, idet den passerer i en vinkel på 45° til den rette linje y = 0 (fig. 4).

Løsning. Fra betingelsen f "(a) = tan 45° finder vi a: a – 3 = 1^a = 4.

1. a = 4 – abscisse af tangentpunktet.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – tangentligning.

Det er let at vise, at løsningen på ethvert andet problem kommer ned til at løse et eller flere nøgleproblemer. Betragt følgende to problemer som et eksempel.

1. Skriv ligningerne for tangenterne til parablen y = 2x 2 – 5x – 2, hvis tangenterne skærer hinanden vinkelret og en af ​​dem rører parablen i punktet med abscisse 3 (fig. 5).

Løsning. Da tangentpunktets abscisse er givet, reduceres den første del af løsningen til nøgleopgave 1.

1. a = 3 – abscisse af tangenspunktet for en af ​​siderne af den rette vinkel.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – ligning for den første tangent.

Lad a – hældningsvinkel for den første tangent. Da tangenterne er vinkelrette, så er hældningsvinklen for den anden tangent. Fra ligningen y = 7x – 20 af den første tangent har vi tg a = 7. Lad os finde

Det betyder, at hældningen af ​​den anden tangent er lig med .

Den videre løsning kommer ned til nøgleopgave 3.

Lad B(c; f(c)) være tangenspunktet for den anden linje, så

1. – abscisse af det andet tangenspunkt.
2.
3.
4.
– ligning for den anden tangent.

Bemærk. Tangensens vinkelkoefficient kan lettere findes, hvis eleverne kender forholdet mellem koefficienterne for vinkelrette linjer k 1 k 2 = – 1.

2. Skriv ligningerne for alle fælles tangenter til graferne for funktioner

Løsning. Opgaven går ud på at finde abscissen af ​​tangentpunkterne for almindelige tangenter, det vil sige at løse nøgleproblem 1 i generel form, tegne et ligningssystem og derefter løse det (fig. 6).

1. Lad a være abscissen af ​​det tangentpunkt, der ligger på grafen for funktionen y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a2.

1. Lad c være abscissen af ​​tangentpunktet, der ligger på grafen for funktionen
2.
3. f "(c) = c.
4.

Da tangenter er generelle, altså

Så y = x + 1 og y = – 3x – 3 er almindelige tangenter.

Hovedmålet med de overvejede opgaver er at forberede eleverne til selvstændigt at genkende typen af ​​nøgleproblem, når de løser mere komplekse problemer, der kræver visse forskningsfærdigheder (evnen til at analysere, sammenligne, generalisere, fremsætte en hypotese osv.). Sådanne opgaver omfatter enhver opgave, hvori nøgleopgaven indgår som en komponent. Lad os som eksempel betragte problemet (omvendt til opgave 1) med at finde en funktion fra familien af ​​dens tangenter.

3. For hvilke b og c tangerer linjerne y = x og y = – 2x grafen for funktionen y = x 2 + bx + c?

Løsning.

Lad t være abscissen af ​​tangenspunktet for den rette linje y = x med parablen y = x 2 + bx + c; p er abscissen af ​​tangenspunktet for den rette linje y = – 2x med parablen y = x 2 + bx + c. Så vil tangentligningen y = x have formen y = (2t + b)x + c – t 2 , og tangentligningen y = – 2x vil have formen y = (2p + b)x + c – p 2 .

Lad os sammensætte og løse et ligningssystem

Svar:

Problemer, der skal løses selvstændigt

1. Skriv ligningerne for tangenterne tegnet til grafen for funktionen y = 2x 2 – 4x + 3 i grafens skæringspunkter med linjen y = x + 3.

Svar: y = – 4x + 3, y = 6x – 9,5.

2. For hvilke værdier af a går tangenten tegnet til grafen for funktionen y = x 2 – ax i punktet af grafen med abscissen x 0 = 1 gennem punktet M(2; 3)?

Svar: a = 0,5.

3. For hvilke værdier af p rører den rette linje y = px – 5 kurven y = 3x 2 – 4x – 2?

Svar: p 1 = – 10, p 2 = 2.

4. Find alle fælles punkter i grafen for funktionen y = 3x – x 3 og tangenten tegnet til denne graf gennem punktet P(0; 16).

Svar: A(2; – 2), B(– 4; 52).

5. Find den korteste afstand mellem parablen y = x 2 + 6x + 10 og den rette linje

Svar:

6. På kurven y = x 2 – x + 1 skal du finde det punkt, hvor tangenten til grafen er parallel med den rette linje y – 3x + 1 = 0.

Svar: M(2; 3).

7. Skriv tangentens ligning til grafen for funktionen y = x 2 + 2x – | 4x |, som rører den ved to punkter. Lav en tegning.

Svar: y = 2x – 4.

8. Bevis, at linjen y = 2x – 1 ikke skærer kurven y = x 4 + 3x 2 + 2x. Find afstanden mellem deres nærmeste punkter.

Svar:

9. På parablen y = x 2 tages to punkter med abscisse x 1 = 1, x 2 = 3. Gennem disse punkter trækkes en sekant. På hvilket punkt af parablen vil tangenten til den være parallel med sekanten? Skriv sekant- og tangentligningerne.

Svar: y = 4x – 3 – sekantsligning; y = 4x – 4 – tangentligning.

10. Find vinklen q mellem tangenterne til grafen for funktionen y = x 3 – 4x 2 + 3x + 1, tegnet i punkterne med abscisse 0 og 1.

Svar: q = 45°.

11. I hvilke punkter danner tangenten til funktionens graf en vinkel på 135° med Ox-aksen?

Svar: A(0; – 1), B(4; 3).

12. Ved punkt A(1; 8) til kurven der tegnes en tangent. Find længden af ​​tangentsegmentet mellem koordinatakserne.

Svar:

13. Skriv ligningen for alle fælles tangenter til graferne for funktionerne y = x 2 – x + 1 og y = 2x 2 – x + 0,5.

Svar: y = – 3x og y = x.

14. Find afstanden mellem tangenterne til funktionens graf parallelt med x-aksen.

Svar:

15. Bestem, i hvilke vinkler parablen y = x 2 + 2x – 8 skærer x-aksen.

Svar: q 1 = arctan 6, q 2 = arctan (– 6).

16. Funktionsgraf find alle punkter, hvor tangenten ved hver af disse til denne graf skærer de positive halvakser af koordinater og afskærer lige store segmenter fra dem.

Svar: A(– 3; 11).

17. Linjen y = 2x + 7 og parablen y = x 2 – 1 skærer hinanden i punkterne M og N. Find skæringspunktet K for linjerne, der tangerer parablen i punkterne M og N.

Svar: K(1; – 9).

18. For hvilke værdier af b tangerer linjen y = 9x + b grafen for funktionen y = x 3 – 3x + 15?

Svar: – 1; 31.

19. For hvilke værdier af k har den rette linje y = kx – 10 kun ét fælles punkt med grafen for funktionen y = 2x 2 + 3x – 2? For de fundne værdier af k skal du bestemme koordinaterne for punktet.

Svar: k 1 = – 5, A(– 2; 0); k2 = 11, B(2; 12).

20. For hvilke værdier af b går tangenten tegnet til grafen for funktionen y = bx 3 – 2x 2 – 4 i punktet med abscissen x 0 = 2 gennem punktet M(1; 8)?

Svar: b = – 3.

21. En parabel med et toppunkt på Ox-aksen berører linjen, der går gennem punkterne A(1; 2) og B(2; 4) ved punkt B. Find parablens ligning.

Svar:

22. Ved hvilken værdi af koefficienten k rører parablen y = x 2 + kx + 1 Ox-aksen?

Svar: k = d 2.

23. Find vinklerne mellem den rette linje y = x + 2 og kurven y = 2x 2 + 4x – 3.

29. Find afstanden mellem tangenterne til funktionens graf og generatorerne med Ox-aksens positive retning i en vinkel på 45°.

Svar:

30. Find stedet for toppunkterne for alle parabler på formen y = x 2 + ax + b, der tangerer linjen y = 4x – 1.

Svar: lige linje y = 4x + 3.

Litteratur

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra og begyndelsen af ​​analyse: 3600 problemer for skolebørn og dem, der går ind på universiteter. – M., Bustard, 1999.
2. Mordkovich A. Seminar fire for unge lærere. Emne: Afledte applikationer. – M., "Matematik", nr. 21/94.
3. Dannelse af viden og færdigheder baseret på teorien om gradvis assimilering af mentale handlinger. / Ed. P.Ya. Galperina, N.F. Talyzina. – M., Moscow State University, 1968.

Eksempel 1. Givet en funktion f(x) = 3x 2 + 4x– 5. Lad os skrive tangentens ligning til grafen for funktionen f(x) ved grafpunktet med abscissen x 0 = 1.

Løsning. Afledt af en funktion f(x) findes for enhver x R . Lad os finde hende:

= (3x 2 + 4x– 5)′ = 6 x + 4.

Derefter f(x 0) = f(1) = 2; (x 0) = = 10. Tangentligningen har formen:

y = (x 0) (x – x 0) + f(x 0),

y = 10(x – 1) + 2,

y = 10x – 8.

Svar. y = 10x – 8.

Eksempel 2. Givet en funktion f(x) = x 3 – 3x 2 + 2x+ 5. Lad os skrive tangentens ligning til grafen for funktionen f(x), parallelt med linjen y = 2x – 11.

Løsning. Afledt af en funktion f(x) findes for enhver x R . Lad os finde hende:

= (x 3 – 3x 2 + 2x+ 5)′ = 3 x 2 – 6x + 2.

Siden tangenten til grafen for funktionen f(x) ved abscissepunktet x 0 er parallel med linjen y = 2x– 11, så er dens hældning lig med 2, dvs. x 0) = 2. Lad os finde denne abscisse ud fra betingelsen, at 3 x– 6x 0 + 2 = 2. Denne lighed er kun gyldig når x 0 = 0 og kl x 0 = 2. Da i begge tilfælde f(x 0) = 5, derefter lige y = 2x + b rører grafen for funktionen enten ved punktet (0; 5) eller ved punktet (2; 5).

I det første tilfælde er den numeriske lighed 5 = 2×0 + sand b, hvor b= 5, og i det andet tilfælde er den numeriske lighed 5 = 2×2 + sand b, hvor b = 1.

Så der er to tangenter y = 2x+ 5 og y = 2x+ 1 til grafen for funktionen f(x), parallelt med linjen y = 2x – 11.

Svar. y = 2x + 5, y = 2x + 1.

Eksempel 3. Givet en funktion f(x) = x 2 – 6x+ 7. Lad os skrive tangentens ligning til grafen for funktionen f(x), der passerer gennem punktet EN (2; –5).

Løsning. Fordi f(2) -5, peg derefter EN hører ikke til grafen for funktionen f(x). Lade x 0 - abscisse af tangentpunktet.

Afledt af en funktion f(x) findes for enhver x R . Lad os finde hende:

= (x 2 – 6x+ 1)′ = 2 x – 6.

Derefter f(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 – 6. Tangentligningen har formen:

y = (2x 0 – 6)(x – x 0) + x– 6x+ 7,

y = (2x 0 – 6)x– x+ 7.

Siden pointen EN hører til tangenten, så er den numeriske lighed sand

–5 = (2x 0 – 6)×2– x+ 7,

hvor x 0 = 0 eller x 0 = 4. Det betyder, at gennem punktet EN du kan tegne to tangenter til grafen for funktionen f(x).

Hvis x 0 = 0, så har tangentligningen formen y = –6x+ 7. Hvis x 0 = 4, så har tangentligningen formen y = 2x – 9.

Svar. y = –6x + 7, y = 2x – 9.

Eksempel 4. Funktioner givet f(x) = x 2 – 2x+ 2 og g(x) = –x 2 – 3. Lad os skrive ligningen for den fælles tangent til graferne for disse funktioner.

Løsning. Lade x 1 - abscisse af tangenspunktet for den ønskede linje med grafen for funktionen f(x), A x 2 - abscisse af tangenspunktet for den samme linje med grafen for funktionen g(x).

Afledt af en funktion f(x) findes for enhver x R . Lad os finde hende:

= (x 2 – 2x+ 2)′ = 2 x – 2.

Derefter f(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 – 2. Tangentligningen har formen:

y = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,

y = (2x 1 – 2)x – x+ 2. (1)

Lad os finde den afledede af funktionen g(x):

= (–x 2 – 3)′ = –2 x.

Lad en funktion f være givet, som på et tidspunkt x 0 har en endelig afledt f (x 0). Så kaldes den rette linje, der går gennem punktet (x 0 ; f (x 0)), med en vinkelkoefficient f ’(x 0), en tangent.

Hvad sker der, hvis den afledede ikke eksisterer i punktet x 0? Der er to muligheder:

1. Der er heller ingen tangent til grafen. Et klassisk eksempel er funktionen y = |x | ved punkt (0; 0).
2. Tangenten bliver lodret. Dette gælder for eksempel for funktionen y = arcsin x i punktet (1; π /2).

Tangentligning

Enhver ikke-lodret ret linje er givet ved en ligning på formen y = kx + b, hvor k er hældningen. Tangenten er ingen undtagelse, og for at sammensætte dens ligning på et tidspunkt x 0, er det nok at kende værdien af ​​funktionen og den afledede på dette tidspunkt.

Så lad en funktion y = f (x) være givet, som har en afledt y = f ’(x) på segmentet. Derefter kan der ved ethvert punkt x 0 ∈ (a ; b) trækkes en tangent til grafen for denne funktion, som er givet af ligningen:

y = f ’(x 0) (x − x 0) + f (x 0)

Her er f ’(x 0) værdien af ​​den afledede i punktet x 0, og f (x 0) er værdien af ​​selve funktionen.

Opgave. Givet funktionen y = x 3 . Skriv en ligning for tangenten til grafen for denne funktion i punktet x 0 = 2.

Tangentligning: y = f ’(x 0) · (x − x 0) + f (x 0). Punktet x 0 = 2 er givet til os, men værdierne f (x 0) og f '(x 0) skal beregnes.

Lad os først finde værdien af ​​funktionen. Alt er nemt her: f (x 0) = f (2) = 2 3 = 8;
Lad os nu finde den afledede: f '(x) = (x 3)' = 3x 2;
Vi erstatter x 0 = 2 i den afledede: f ’(x 0) = f ’(2) = 3 2 2 = 12;
I alt får vi: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Dette er tangentligningen.

Opgave. Skriv en ligning for tangenten til grafen for funktionen f (x) = 2sin x + 5 i punktet x 0 = π /2.

Denne gang vil vi ikke beskrive hver handling i detaljer - vi vil kun angive de vigtigste trin. Vi har:

f (x 0) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;
f '(x) = (2sin x + 5)' = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Tangentligning:

y = 0 · (x − π /2) + 7 ⇒ y = 7

I sidstnævnte tilfælde viste den lige linje sig at være vandret, fordi dens vinkelkoefficient k = 0. Der er ikke noget galt med dette - vi faldt lige over et ekstremum.

En tangent er en ret linje , som berører grafen for funktionen på et punkt, og alle punkter er i den korteste afstand fra funktionens graf. Derfor passerer tangenten tangent til funktionens graf i en bestemt vinkel, og flere tangenter i forskellige vinkler kan ikke passere gennem tangenspunktet. Tangentligninger og normale ligninger til grafen for en funktion konstrueres ved hjælp af den afledede.

Tangentligningen er afledt af linjeligningen .

Lad os udlede tangentens ligning og derefter normalens ligning til funktionens graf.

y = kx + b .

I ham k- vinkelkoefficient.

Herfra får vi følgende indgang:

y - y 0 = k(x - x 0 ) .

Afledt værdi f "(x 0 ) funktioner y = f(x) på punktet x0 lige med hældning k= tg φ tangent til grafen for en funktion tegnet gennem et punkt M0 (x 0 , y 0 ) , Hvor y0 = f(x 0 ) . Dette er geometrisk betydning afledte .

Dermed kan vi erstatte k på f "(x 0 ) og få følgende ligning af tangenten til grafen for en funktion :

y - y 0 = f "(x 0 )(x - x 0 ) .

I problemer, der involverer at sammensætte ligningen for en tangent til grafen for en funktion (og vi vil snart gå videre til dem), er det nødvendigt at reducere ligningen opnået fra ovenstående formel til ligning af en ret linje i generel form. For at gøre dette skal du flytte alle bogstaver og tal til venstre side af ligningen og lade nul på højre side.

Nu om den normale ligning. Normal - dette er en ret linje, der går gennem tangenspunktet til grafen for funktionen vinkelret på tangenten. Normal ligning :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

For at varme op bliver du bedt om selv at løse det første eksempel, og derefter se på løsningen. Der er al mulig grund til at håbe, at denne opgave ikke bliver et "koldt brusebad" for vores læsere.

Eksempel 0. Opret en tangentligning og en normalligning for grafen for en funktion i et punkt M (1, 1) .

Eksempel 1. Skriv en tangentligning og en normalligning til grafen for en funktion , hvis abscissen er tangent.

Lad os finde den afledede af funktionen:

Nu har vi alt, der skal erstattes i indtastningen i den teoretiske hjælp for at få tangentligningen. Vi får

I dette eksempel var vi heldige: hældningen viste sig at være nul, så vi reducerer ligningen separat til generelle udseende var ikke nødvendigt. Nu kan vi lave den normale ligning:

I figuren nedenfor: graf over en funktion i bordeaux farve, tangent Grøn farve, orange normal.

Det næste eksempel er heller ikke kompliceret: Funktionen, som i det foregående, er også et polynomium, men hældningen vil ikke være lig med nul, så et trin mere vil blive tilføjet - hvilket bringer ligningen til en generel form.

Eksempel 2.

Løsning. Lad os finde ordinaten til tangentpunktet:

Lad os finde den afledede af funktionen:

.

Lad os finde værdien af ​​den afledede ved tangenspunktet, det vil sige hældningen af ​​tangenten:

Vi erstatter alle de opnåede data i den "blanke formel" og får tangentligningen:

Vi bringer ligningen til dens generelle form (vi samler alle bogstaver og tal bortset fra nul på venstre side og lader nul til højre):

Vi sammensætter normalligningen:

Eksempel 3. Skriv en tangentligning og en normalligning til funktionens graf, hvis abscissen er tangentpunktet.

Løsning. Lad os finde ordinaten til tangentpunktet:

Lad os finde den afledede af funktionen:

.

Lad os finde værdien af ​​den afledede ved tangenspunktet, det vil sige hældningen af ​​tangenten:

.

Vi finder tangentligningen:

Før du bringer ligningen til dens generelle form, skal du "kæmme den" lidt: gange led for led med 4. Vi gør dette og bringer ligningen til dens generelle form:

Vi sammensætter normalligningen:

Eksempel 4. Skriv en tangentligning og en normalligning til funktionens graf, hvis abscissen er tangentpunktet.

Løsning. Lad os finde ordinaten til tangentpunktet:

.

Lad os finde den afledede af funktionen:

Lad os finde værdien af ​​den afledede ved tangenspunktet, det vil sige hældningen af ​​tangenten:

.

Vi får tangentligningen:

Vi bringer ligningen til sin generelle form:

Vi sammensætter normalligningen:

En almindelig fejl, når man skriver tangent- og normalligninger, er ikke at bemærke, at funktionen givet i eksemplet er kompleks, og at beregne dens afledte som den afledede af en simpel funktion. De følgende eksempler er allerede fra komplekse funktioner(den tilsvarende lektion åbner i et nyt vindue).

Eksempel 5. Skriv en tangentligning og en normalligning til funktionens graf, hvis abscissen er tangentpunktet.

Løsning. Lad os finde ordinaten til tangentpunktet:

Opmærksomhed! Denne funktion er kompleks, da tangentargumentet (2 x) er i sig selv en funktion. Derfor finder vi den afledede af en funktion som den afledede af en kompleks funktion.

Y = f(x) og hvis der på dette punkt kan trækkes en tangent til grafen for funktionen, som ikke er vinkelret på abscisseaksen, så er tangentens vinkelkoefficient lig f"(a). Vi har allerede brugt dette flere gange For eksempel blev det i § 33 fastslået, at grafen for funktionen y = sin x (sinusformet) ved origo danner en vinkel på 45° med x-aksen (mere præcist, tangenten til den. graf ved origo danner en vinkel på 45° med x-aksens positive retning), og i eksempel 5 blev § 33 punkter fundet på skema givet funktioner, hvor tangenten er parallel med x-aksen. I eksempel 2 i § 33 blev der udarbejdet en ligning for tangenten til grafen for funktionen y = x 2 i punktet x = 1 (mere præcist i punktet (1; 1), men oftere er det kun abscisseværdien, der er angivet, idet man mener, at hvis abscisseværdien er kendt, så kan ordinatværdien findes ud fra ligningen y = f(x)). I dette afsnit vil vi udvikle en algoritme til at sammensætte en tangentligning til grafen for enhver funktion.

Lad funktionen y = f(x) og punktet M (a; f(a)) være givet, og lad det også være kendt, at f"(a) eksisterer. Lad os lave en ligning for tangenten til grafen givet funktion på et givet tidspunkt. Denne ligning har ligesom ligningen for enhver ret linje, der ikke er parallel med ordinataksen, formen y = kx+m, så opgaven er at finde værdierne af koefficienterne k og m.

Der er ingen problemer med vinkelkoefficienten k: vi ved, at k = f "(a). For at beregne værdien af ​​m bruger vi det faktum, at den ønskede rette linje går gennem punktet M(a; f (a)) Det betyder, at hvis vi erstatter koordinatpunktet M i ligningen for den rette linje, får vi den rigtige lighed: f(a) = ka+m, hvorfra vi finder, at m = f(a) - ka.
Det er tilbage at erstatte de fundne værdier af kitkoefficienterne i ligningen lige:

Vi har fået ligningen for tangenten til grafen for funktionen y = f(x) i punktet x=a.
Hvis f.eks.
Ved at erstatte de fundne værdier a = 1, f(a) = 1 f"(a) = 2 i ligning (1), får vi: y = 1+2(x-f), dvs. y = 2x-1.
Sammenlign dette resultat med det opnåede i eksempel 2 fra § 33. Naturligvis skete det samme.
Lad os lave en ligning for tangenten til grafen for funktionen y = tan x ved origo. Vi har: dette betyder cos x f"(0) = 1. Ved at erstatte de fundne værdier a = 0, f(a) = 0, f"(a) = 1 i ligning (1), får vi: y = x.
Derfor tegnede vi tangentoiden i § 15 (se fig. 62) gennem koordinaternes begyndelse i en vinkel på 45° i forhold til abscisseaksen.
Løser disse nok simple eksempler, brugte vi faktisk en bestemt algoritme, som er indeholdt i formel (1). Lad os gøre denne algoritme eksplicit.

ALGORIME TIL UDVIKLING AF EN LIGNING FOR EN TANGENT TIL GRAFEN FOR FUNKTIONEN y = f(x)

1) Udpeg abscissen af ​​tangenspunktet med bogstavet a.
2) Beregn 1 (a).
3) Find f"(x) og beregn f"(a).
4) Erstat de fundne tal a, f(a), (a) med formel (1).

Eksempel 1. Skriv en ligning for tangenten til grafen for funktionen i punktet x = 1.
Lad os bruge algoritmen under hensyntagen til det i i dette eksempel

I fig. 126 er en hyperbel afbildet, en ret linje y = 2 er konstrueret.
Tegningen bekræfter ovenstående beregninger: faktisk rører linjen y = 2 hyperbelen ved punktet (1; 1).

Svar: y = 2-x.
Eksempel 2. Tegn en tangent til grafen for funktionen, så den er parallel med linjen y = 4x - 5.
Lad os afklare problemformuleringen. Kravet om at "tegne en tangent" betyder normalt "at danne en ligning for tangenten." Dette er logisk, for hvis en person var i stand til at skabe en ligning for en tangent, så er det usandsynligt, at han har svært ved at konstruere en ret linje på koordinatplanet ved hjælp af dens ligning.
Lad os bruge algoritmen til at sammensætte tangentligningen, idet vi tager højde for, at i dette eksempel. Men i modsætning til det foregående eksempel er der tvetydighed: tangentpunktets abscisse er ikke eksplicit angivet.
Lad os begynde at tænke sådan her. Den ønskede tangent skal være parallel med den rette linje y = 4x-5. To linjer er parallelle, hvis og kun hvis deres hældninger er lige store. Det betyder, at tangens vinkelkoefficient skal være lig med vinkelkoefficienten for den givne rette linje: Således kan vi finde værdien af ​​a ud fra ligningen f"(a) = 4.
Vi har:
Ud fra ligningen Det betyder, at der er to tangenter, der opfylder problemets betingelser: den ene i punktet med abscisse 2, den anden i punktet med abscisse -2.
Nu kan du følge algoritmen.

Eksempel 3. Fra punkt (0; 1) tegnes en tangent til grafen for funktionen
Lad os bruge algoritmen til at sammensætte tangentligningen, idet vi tager højde for, at i dette eksempel, Bemærk, at her, som i eksempel 2, er abscissen af ​​tangentpunktet ikke eksplicit angivet. Ikke desto mindre følger vi algoritmen.

Ved betingelse passerer tangenten gennem punktet (0; 1). Ved at erstatte værdierne x = 0, y = 1 i ligning (2), får vi:
Som du kan se, i dette eksempel, lykkedes det kun på det fjerde trin af algoritmen at finde abscissen af ​​tangentpunktet. Ved at erstatte værdien a =4 i ligning (2), får vi:

I fig. 127 præsenterer en geometrisk illustration af det betragtede eksempel: en graf over funktionen er plottet

I § ​​32 bemærkede vi, at for en funktion y = f(x) med en afledt i et fast punkt x, er den omtrentlige lighed gyldig:

For at gøre det nemmere for yderligere ræsonnementer, lad os ændre notationen: i stedet for x skriver vi a, i stedet for vil vi skrive x og følgelig i stedet for vil vi skrive x-a. Så vil den omtrentlige lighed skrevet ovenfor have formen:

Se nu på fig. 128. Der tegnes en tangent til grafen for funktionen y = f(x) i punktet M (a; f (a)). Punkt x er markeret på x-aksen tæt på a. Det er tydeligt, at f(x) er ordinaten til grafen for funktionen i specificeret punkt X. Hvad er f(a) + f"(a) (x-a)? Dette er ordinaten af ​​tangenten svarende til det samme punkt x - se formel (1). Hvad er meningen med den omtrentlige lighed (3)? Faktum at For at beregne den omtrentlige værdi af funktionen, tag ordinatværdien af ​​tangenten.

Eksempel 4. Find den omtrentlige værdi numerisk udtryk 1,02 7 .
Det handler om om at finde værdien af ​​funktionen y = x 7 i punktet x = 1,02. Lad os bruge formel (3), idet vi tager højde for det i dette eksempel
Som et resultat får vi:

Hvis vi bruger en lommeregner, får vi: 1,02 7 = 1,148685667...
Som du kan se, er tilnærmelsesnøjagtigheden ganske acceptabel.
Svar: 1,02 7 =1,14.

A.G. Mordkovich Algebra 10 klasse

Kalendertematisk planlægning i matematik, video i matematik online, Matematik i skolen download

Lektionens indhold lektionsnotater understøttende frame lektion præsentation acceleration metoder interaktive teknologier Øve sig opgaver og øvelser selvtest workshops, træninger, cases, quests lektier diskussion spørgsmål retoriske spørgsmål fra elever Illustrationer lyd, videoklip og multimedier fotografier, billeder, grafik, tabeller, diagrammer, humor, anekdoter, vittigheder, tegneserier, lignelser, ordsprog, krydsord, citater Tilføjelser abstracts artikler tricks for de nysgerrige krybber lærebøger grundlæggende og yderligere ordbog over begreber andet Forbedring af lærebøger og lektionerrette fejl i lærebogen opdatering af et fragment i en lærebog, elementer af innovation i lektionen, udskiftning af forældet viden med ny Kun for lærere perfekte lektioner kalenderplan for året retningslinier diskussionsprogrammer Integrerede lektioner