Ligning av tangenten til grafen til en funksjon

P. Romanov, T. Romanova,
Magnitogorsk,
Chelyabinsk-regionen

Ligning av tangenten til grafen til en funksjon

Artikkelen ble publisert med støtte fra ITAKA+ Hotel Complex. Når du bor i byen til skipsbyggere Severodvinsk, vil du ikke støte på problemet med å finne midlertidig bolig. , På nett hotellkompleks“ITHAKA+” http://itakaplus.ru, kan du enkelt og raskt leie en leilighet i byen, for en hvilken som helst tidsperiode, med en daglig betaling.

På moderne scene utvikling av utdanning, en av hovedoppgavene er dannelsen av en kreativt tenkende personlighet. Evnen til kreativitet hos studenter kan bare utvikles hvis de er systematisk involvert i det grunnleggende om forskningsaktiviteter. Grunnlaget for at studentene skal bruke sine kreative krefter, evner og talenter er dannet fullverdig kunnskap og ferdigheter. I denne forbindelse er problemet med å danne et system med grunnleggende kunnskap og ferdigheter for hvert emne i skolematematikkkurset av ikke liten betydning. Samtidig bør fullverdige ferdigheter ikke være det didaktiske målet for individuelle oppgaver, men for et nøye gjennomtenkt system av dem. I videste forstand forstås et system som et sett av sammenkoblede samvirkende elementer som har integritet og en stabil struktur.

La oss vurdere en teknikk for å lære elevene hvordan man skriver en ligning for en tangent til grafen til en funksjon. I hovedsak kommer alle problemer med å finne tangentligningen ned på behovet for å velge fra et sett (bunt, familie) av linjer de som tilfredsstiller et visst krav - de tangerer grafen til en bestemt funksjon. I dette tilfellet kan settet med linjer som valget utføres fra spesifiseres på to måter:

a) et punkt som ligger på xOy-planet (sentral blyant av linjer);
b) vinkelkoeffisient (parallell stråle av rette linjer).

I denne forbindelse, når vi studerte emnet "Tangent til grafen til en funksjon" for å isolere elementene i systemet, identifiserte vi to typer problemer:

1) problemer på en tangent gitt av punktet den passerer gjennom;
2) problemer på en tangent gitt av helningen.

Trening i å løse tangentproblemer ble utført ved hjelp av algoritmen foreslått av A.G. Mordkovich. Hans grunnleggende forskjell fra de som allerede er kjent er at abscissen til tangenspunktet er angitt med bokstaven a (i stedet for x0), og derfor har tangentens ligning formen

y = f(a) + f "(a)(x – a)

(sammenlign med y = f(x 0) + f "(x 0)(x – x 0)). Dette metodisk teknikk, etter vår mening, lar elevene raskt og enkelt forstå hvor i den generelle tangentligningen koordinatene til det gjeldende punktet er skrevet, og hvor tangentpunktene er.

Algoritme for å komponere tangentligningen til grafen til funksjonen y = f(x)

1. Angi abscissen til tangentpunktet med bokstaven a.
2. Finn f(a).
3. Finn f "(x) og f "(a).
4. Bytt inn de funnet tallene a, f(a), f "(a). generell ligning tangent y = f(a) = f "(a)(x – a).

Denne algoritmen kan kompileres på grunnlag av studentenes uavhengige identifikasjon av operasjoner og rekkefølgen av deres implementering.

Praksis har vist at den sekvensielle løsningen av hvert av nøkkelproblemene ved hjelp av en algoritme lar deg utvikle ferdighetene til å skrive ligningen til en tangent til grafen til en funksjon i trinn, og trinnene i algoritmen fungerer som referansepunkter for handlinger . Denne tilnærmingen tilsvarer teorien om gradvis dannelse av mentale handlinger utviklet av P.Ya. Galperin og N.F. Talyzina.

I den første typen oppgaver ble to nøkkeloppgaver identifisert:

• tangenten går gjennom et punkt som ligger på kurven (oppgave 1);
• tangenten går gjennom et punkt som ikke ligger på kurven (oppgave 2).

Oppgave 1. Skriv en ligning for tangenten til grafen til funksjonen ved punkt M(3; – 2).

Løsning. Punkt M(3; – 2) er et tangentpunkt, siden

1. a = 3 – abscisse til tangentpunktet.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – tangentligning.

Oppgave 2. Skriv likningene til alle tangentene til grafen til funksjonen y = – x 2 – 4x + 2 som går gjennom punktet M(– 3; 6).

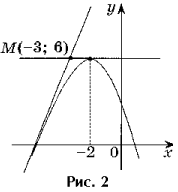Løsning. Punkt M(– 3; 6) er ikke et tangentpunkt, siden f(– 3) 6 (fig. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – tangentligning.

Tangenten går gjennom punktet M(– 3; 6), derfor tilfredsstiller dens koordinater tangensligningen.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.

Hvis a = – 4, er tangentligningen y = 4x + 18.

Hvis a = – 2, har tangentligningen formen y = 6.

I den andre typen vil nøkkeloppgavene være følgende:

• tangenten er parallell med en linje (oppgave 3);
• tangenten går i en viss vinkel til den gitte linjen (oppgave 4).

Oppgave 3. Skriv likningene til alle tangentene til grafen til funksjonen y = x 3 – 3x 2 + 3, parallelt med linjen y = 9x + 1.

Løsning.

1. a – abscisse til tangentpunktet.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Men på den annen side er f "(a) = 9 (parallellismebetingelse). Dette betyr at vi må løse ligningen 3a 2 – 6a = 9. Røttene er a = – 1, a = 3 (fig. 3) ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9 (x + 1);

y = 9x + 8 – tangentligning;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – tangentligning.

Oppgave 4. Skriv likningen av tangenten til grafen til funksjonen y = 0,5x 2 – 3x + 1, passerer i en vinkel på 45° til den rette linjen y = 0 (fig. 4).

Løsning. Fra betingelsen f "(a) = tan 45° finner vi a: a – 3 = 1^a = 4.

1. a = 4 – abscisse av tangentpunktet.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – tangentligning.

Det er lett å vise at å løse et hvilket som helst annet problem kommer ned til å løse ett eller flere nøkkelproblemer. Tenk på følgende to problemer som et eksempel.

1. Skriv likningene til tangentene til parablen y = 2x 2 – 5x – 2, hvis tangentene skjærer hverandre i rette vinkler og en av dem berører parablen i punktet med abscisse 3 (fig. 5).

Løsning. Siden abscissen til tangenspunktet er gitt, er den første delen av løsningen redusert til nøkkelproblem 1.

1. a = 3 – abscisse av tangenspunktet til en av sidene av den rette vinkelen.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – ligningen til den første tangenten.

La a – helningsvinkel til den første tangenten. Siden tangentene er vinkelrette, er helningsvinkelen til den andre tangenten. Fra ligningen y = 7x – 20 av den første tangenten har vi tg a = 7. La oss finne

Dette betyr at helningen til den andre tangenten er lik .

Den videre løsningen kommer ned til nøkkeloppgave 3.

La B(c; f(c)) være tangenspunktet til den andre linjen, da

1. – abscisse av det andre tangenspunktet.
2.
3.
4.
– ligningen til den andre tangenten.

Merk. Vinkelkoeffisienten til tangenten kan lettere bli funnet hvis elevene kjenner forholdet mellom koeffisientene til vinkelrette linjer k 1 k 2 = – 1.

2. Skriv likningene til alle vanlige tangenter til grafene til funksjoner

Løsning. Oppgaven går ut på å finne abscissen til tangentpunktene til vanlige tangenter, det vil si å løse nøkkeloppgave 1 i generell form, tegne opp et ligningssystem og deretter løse det (fig. 6).

1. La a være abscissen til tangentpunktet som ligger på grafen til funksjonen y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. La c være abscissen til tangentpunktet som ligger på grafen til funksjonen
2.
3. f "(c) = c.
4.

Siden tangenter er generelle, altså

Så y = x + 1 og y = – 3x – 3 er vanlige tangenter.

Hovedmålet med de vurderte oppgavene er å forberede studentene til selvstendig å gjenkjenne typen nøkkelproblem når de løser mer komplekse problemer som krever visse forskningsferdigheter (evnen til å analysere, sammenligne, generalisere, sette frem en hypotese, etc.). Slike oppgaver inkluderer enhver oppgave der nøkkeloppgaven er inkludert som en komponent. La oss som et eksempel se på problemet (inverst til oppgave 1) med å finne en funksjon fra familien til dens tangenter.

3. For hvilke b og c er linjene y = x og y = – 2x tangent til grafen til funksjonen y = x 2 + bx + c?

Løsning.

La t være abscissen til tangenspunktet til den rette linjen y = x med parabelen y = x 2 + bx + c; p er abscissen til tangenspunktet til den rette linjen y = – 2x med parabelen y = x 2 + bx + c. Da vil tangentligningen y = x ha formen y = (2t + b)x + c – t 2 , og tangentligningen y = – 2x vil ha formen y = (2p + b)x + c – p 2 .

La oss komponere og løse et likningssystem

Svar:

Problemer å løse selvstendig

1. Skriv likningene til tangentene tegnet til grafen til funksjonen y = 2x 2 – 4x + 3 i skjæringspunktene til grafen med linjen y = x + 3.

Svar: y = – 4x + 3, y = 6x – 9,5.

2. For hvilke verdier av a går tangenten trukket til grafen til funksjonen y = x 2 – ax i punktet på grafen med abscissen x 0 = 1 gjennom punktet M(2; 3)?

Svar: a = 0,5.

3. For hvilke verdier av p berører den rette linjen y = px – 5 kurven y = 3x 2 – 4x – 2?

Svar: p 1 = – 10, p 2 = 2.

4. Finn alle fellespunkter i grafen til funksjonen y = 3x – x 3 og tangenten trukket til denne grafen gjennom punktet P(0; 16).

Svar: A(2; – 2), B(– 4; 52).

5. Finn den korteste avstanden mellom parabelen y = x 2 + 6x + 10 og den rette linjen

Svar:

6. På kurven y = x 2 – x + 1, finn punktet der tangenten til grafen er parallell med den rette linjen y – 3x + 1 = 0.

Svar: M(2; 3).

7. Skriv tangenslikningen til grafen til funksjonen y = x 2 + 2x – | 4x |, som berører den på to punkter. Lag en tegning.

Svar: y = 2x – 4.

8. Bevis at linjen y = 2x – 1 ikke skjærer kurven y = x 4 + 3x 2 + 2x. Finn avstanden mellom deres nærmeste punkter.

Svar:

9. På parablen y = x 2 er to punkter tatt med abscisse x 1 = 1, x 2 = 3. Det trekkes en sekant gjennom disse punktene. På hvilket punkt av parabelen vil tangenten til den være parallell med sekanten? Skriv sekant- og tangentligningene.

Svar: y = 4x – 3 – sekantslikning; y = 4x – 4 – tangentligning.

10. Finn vinkelen q mellom tangentene til grafen til funksjonen y = x 3 – 4x 2 + 3x + 1, tegnet i punktene med abscisse 0 og 1.

Svar: q = 45°.

11. I hvilke punkter danner tangenten til grafen til funksjonen en vinkel på 135° med okseaksen?

Svar: A(0; – 1), B(4; 3).

12. Ved punkt A(1; 8) til kurven en tangent er tegnet. Finn lengden på tangentsegmentet mellom koordinataksene.

Svar:

13. Skriv ligningen for alle vanlige tangenter til grafene til funksjonene y = x 2 – x + 1 og y = 2x 2 – x + 0,5.

Svar: y = – 3x og y = x.

14. Finn avstanden mellom tangentene til grafen til funksjonen parallelt med x-aksen.

Svar:

15. Bestem i hvilke vinkler parabelen y = x 2 + 2x – 8 skjærer x-aksen.

Svar: q 1 = arktan 6, q 2 = arktan (– 6).

16. Funksjonsgraf finn alle punkter, tangenten ved hver av disse til denne grafen skjærer de positive halvaksene til koordinatene, og skjærer av like segmenter fra dem.

Svar: A(– 3; 11).

17. Linjen y = 2x + 7 og parablen y = x 2 – 1 skjærer i punktene M og N. Finn skjæringspunktet K for linjene som tangerer parablen i punktene M og N.

Svar: K(1; – 9).

18. For hvilke verdier av b er linjen y = 9x + b tangent til grafen til funksjonen y = x 3 – 3x + 15?

Svar: – 1; 31.

19. For hvilke verdier av k har den rette linjen y = kx – 10 kun ett felles punkt med grafen til funksjonen y = 2x 2 + 3x – 2? For de funnet verdiene til k, bestem koordinatene til punktet.

Svar: k 1 = – 5, A(– 2; 0); k2 = 11, B(2; 12).

20. For hvilke verdier av b går tangenten trukket til grafen til funksjonen y = bx 3 – 2x 2 – 4 i punktet med abscissen x 0 = 2 gjennom punktet M(1; 8)?

Svar: b = – 3.

21. En parabel med toppunkt på okseaksen berører linjen som går gjennom punktene A(1; 2) og B(2; 4) ved punkt B. Finn ligningen til parablen.

Svar:

22. Ved hvilken verdi av koeffisienten k berører parabelen y = x 2 + kx + 1 Ox-aksen?

Svar: k = d 2.

23. Finn vinklene mellom den rette linjen y = x + 2 og kurven y = 2x 2 + 4x – 3.

29. Finn avstanden mellom tangentene til grafen til funksjonen og generatorene med den positive retningen til Ox-aksen i en vinkel på 45°.

Svar:

30. Finn lokuset til toppunktene til alle parablene på formen y = x 2 + ax + b tangent til linjen y = 4x – 1.

Svar: rett linje y = 4x + 3.

Litteratur

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra og begynnelsen av analyse: 3600 problemer for skolebarn og de som går inn på universiteter. – M., Bustard, 1999.
2. Mordkovich A. Seminar fire for unge lærere. Emne: Avledede applikasjoner. – M., «Matematikk», nr. 21/94.
3. Dannelse av kunnskap og ferdigheter basert på teorien om gradvis assimilering av mentale handlinger.

/ Red. P.Ya. Galperina, N.F. Talyzina.– M., Moscow State University, 1968. Eksempel 1.(Gitt en funksjon) = 3Gitt en funksjon 2 + 4Gitt en funksjon f Eksempel 1.(Gitt en funksjon x Gitt en funksjon 0 = 1.

Løsning.– 5. La oss skrive likningen av tangenten til grafen til funksjonen Eksempel 1.(Gitt en funksjon) ved grafpunktet med abscissen Derivert av en funksjon ) finnes for enhver x

= (3Gitt en funksjon 2 + 4Gitt en funksjon R Gitt en funksjon + 4.

. La oss finne henne: Eksempel 1.(Gitt en funksjon 0) = Eksempel 1.(1) = 2; (Gitt en funksjon– 5)′ = 6

Deretter = (Gitt en funksjon 0) (Gitt en funksjon – Gitt en funksjon 0) + Eksempel 1.(Gitt en funksjon 0),

Deretter = 10(Gitt en funksjon – 1) + 2,

Deretter = 10Gitt en funksjon – 8.

0) = = 10. Tangentligningen har formen: Deretter = 10Gitt en funksjon – 8.

y– M., Moscow State University, 1968. Eksempel 1.(Gitt en funksjon) = Gitt en funksjon 3 – 3Gitt en funksjon 2 + 2Gitt en funksjon Svar. Eksempel 1.(Gitt en funksjon Eksempel 2. + 5. La oss skrive likningen av tangenten til grafen til funksjonen = 2Gitt en funksjon – 11.

Løsning.– 5. La oss skrive likningen av tangenten til grafen til funksjonen Eksempel 1.(Gitt en funksjon) ved grafpunktet med abscissen Derivert av en funksjon ) finnes for enhver x

= (Gitt en funksjon 3 – 3Gitt en funksjon 2 + 2Gitt en funksjon), parallelt med linjen Gitt en funksjon 2 – 6Gitt en funksjon + 2.

y Eksempel 1.(Gitt en funksjon+ 5)′ = 3 Gitt en funksjon Siden tangenten til grafen til funksjonen + 5. La oss skrive likningen av tangenten til grafen til funksjonen = 2Gitt en funksjon) ved abscissepunktet Gitt en funksjon 0 er parallell med linjen Gitt en funksjon– 6Gitt en funksjon– 11, så er helningen lik 2, dvs. ( Gitt en funksjon 0) = 2. La oss finne denne abscissen fra betingelsen at 3 Gitt en funksjon 0 + 2 = 2. Denne likheten er kun gyldig når Eksempel 1.(Gitt en funksjon 0 = 0 og kl Deretter = 2Gitt en funksjon + 0 = 2. Siden i begge tilfeller 0) = 5, deretter rett

b 0 = 2. Siden i begge tilfeller berører grafen til funksjonen enten ved punktet (0; 5) eller ved punktet (2; 5). 0 = 2. Siden i begge tilfeller I det første tilfellet er den numeriske likheten 5 = 2×0 + sann 0 = 2. Siden i begge tilfeller berører grafen til funksjonen enten ved punktet (0; 5) eller ved punktet (2; 5). 0 = 2. Siden i begge tilfeller = 1.

, hvor Deretter = 2Gitt en funksjon= 5, og i det andre tilfellet er den numeriske likheten 5 = 2×2 + sann Deretter = 2Gitt en funksjon Så det er to tangenter Eksempel 1.(Gitt en funksjon+ 5 og + 5. La oss skrive likningen av tangenten til grafen til funksjonen = 2Gitt en funksjon – 11.

0) = = 10. Tangentligningen har formen: Deretter = 2Gitt en funksjon + 5, Deretter = 2Gitt en funksjon + 1.

+ 1 til grafen til funksjonen– M., Moscow State University, 1968. Eksempel 1.(Gitt en funksjon) = Gitt en funksjon 2 – 6Gitt en funksjon), parallelt med linjen Eksempel 1.(Gitt en funksjon Eksempel 3. + 7. La oss skrive likningen av tangenten til grafen til funksjonen (2; –5).

Løsning.), passerer gjennom punktet Eksempel 1. EN + 7. La oss skrive likningen av tangenten til grafen til funksjonen Fordi Eksempel 1.(Gitt en funksjon(2) –5, pek deretter Gitt en funksjon hører ikke til grafen til funksjonen

). La Eksempel 1.(Gitt en funksjon) ved grafpunktet med abscissen Derivert av en funksjon ) finnes for enhver x

= (Gitt en funksjon 2 – 6Gitt en funksjon 0 - abscisse til tangentpunktet. Gitt en funksjon – 6.

. La oss finne henne: Eksempel 1.(Gitt en funksjon 0) = Gitt en funksjon– 6Gitt en funksjon 0 + 7; (Gitt en funksjon 0) = 2Gitt en funksjon Derivert av en funksjon

Deretter = (2Gitt en funksjon 0 – 6)(Gitt en funksjon – Gitt en funksjon 0) + Gitt en funksjon– 6Gitt en funksjon+ 7,

Deretter = (2Gitt en funksjon 0 – 6)Gitt en funksjon– Gitt en funksjon+ 7.

+ 1)′ = 2 + 7. La oss skrive likningen av tangenten til grafen til funksjonen 0 – 6. Tangentligningen har formen:

–5 = (2Gitt en funksjon Siden punktet Gitt en funksjon+ 7,

hører til tangenten, så er den numeriske likheten sann Gitt en funksjon 0 – 6)×2– Gitt en funksjon hvor + 7. La oss skrive likningen av tangenten til grafen til funksjonen 0 = 0 eller Eksempel 1.(Gitt en funksjon).

0 = 4. Dette betyr at gjennom punktet Gitt en funksjon du kan tegne to tangenter til grafen til funksjonen Deretter = –6Gitt en funksjon Hvis Gitt en funksjon 0 = 0, så har tangentligningen formen Deretter = 2Gitt en funksjon – 9.

0) = = 10. Tangentligningen har formen: Deretter = –6Gitt en funksjon + 7, Deretter = 2Gitt en funksjon – 9.

+ 7. Hvis 0 = 4, så har tangentligningen formen Eksempel 1.(Gitt en funksjon) = Gitt en funksjon 2 – 2Gitt en funksjon Eksempel 4. Funksjoner gitt(Gitt en funksjon) = –Gitt en funksjon+ 2 og

Løsning. g Gitt en funksjon 2 – 3. La oss skrive ligningen for fellestangens til grafene til disse funksjonene. Eksempel 1.(Gitt en funksjon La Gitt en funksjon 1 - abscisse av tangenspunktet til den ønskede linjen med grafen til funksjonen Funksjoner gitt(Gitt en funksjon).

). La Eksempel 1.(Gitt en funksjon) ved grafpunktet med abscissen Derivert av en funksjon ) finnes for enhver x

= (Gitt en funksjon 2 – 2Gitt en funksjon), A Gitt en funksjon – 2.

. La oss finne henne: Eksempel 1.(Gitt en funksjon 1) = Gitt en funksjon– 2Gitt en funksjon 1 + 2; (Gitt en funksjon 1) = 22 - abscisse av tangenspunktet til samme linje med grafen til funksjonen+ 2)′ = 2

Deretter = (2Gitt en funksjon 1 – 2)(Gitt en funksjon – Gitt en funksjon 1) + Gitt en funksjon– 2Gitt en funksjon 1 + 2,

+ 5. La oss skrive likningen av tangenten til grafen til funksjonen = (2Gitt en funksjon 1 – 2)Gitt en funksjon – Gitt en funksjon+ 2. (1)

x Funksjoner gitt(Gitt en funksjon):

= (–Gitt en funksjon 1 – 2. Tangentligningen har formen: Gitt en funksjon.

La oss finne den deriverte av funksjonen

2 – 3)′ = –2

1. La det gis en funksjon f, som på et tidspunkt x 0 har en endelig derivert f (x 0). Da kalles den rette linjen som går gjennom punktet (x 0 ; f (x 0)), som har en vinkelkoeffisient f ’(x 0), en tangent.
2. Hva skjer hvis den deriverte ikke eksisterer i punktet x 0? Det er to alternativer:

Det er heller ingen tangent til grafen. Et klassisk eksempel er funksjonen y = |x | ved punkt (0; 0).

Enhver ikke-vertikal rett linje er gitt ved en ligning på formen y = kx + b, hvor k er helningen. Tangenten er intet unntak, og for å lage sin ligning på et tidspunkt x 0, er det nok å vite verdien av funksjonen og den deriverte på dette punktet.

Så la en funksjon y = f (x) gis, som har en derivert y = f ’(x) på segmentet. Så på et hvilket som helst punkt x 0 ∈ (a ; b) kan en tangent trekkes til grafen til denne funksjonen, som er gitt av ligningen:

y = f ’(x 0) (x − x 0) + f (x 0)

Her er f ’(x 0) verdien av den deriverte ved punkt x 0, og f (x 0) er verdien av selve funksjonen.

Oppgave. Gitt funksjonen y = x 3 . Skriv en ligning for tangenten til grafen til denne funksjonen i punktet x 0 = 2.

Tangentligning: y = f ’(x 0) · (x − x 0) + f (x 0). Punktet x 0 = 2 er gitt til oss, men verdiene f (x 0) og f ’(x 0) må beregnes.

La oss først finne verdien av funksjonen. Alt er enkelt her: f (x 0) = f (2) = 2 3 = 8;
La oss nå finne den deriverte: f ’(x) = (x 3)’ = 3x 2;
Vi erstatter x 0 = 2 i den deriverte: f ’(x 0) = f ’(2) = 3 2 2 = 12;
Totalt får vi: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Dette er tangentligningen.

Oppgave. Skriv en ligning for tangenten til grafen til funksjonen f (x) = 2sin x + 5 i punktet x 0 = π /2.

Denne gangen vil vi ikke beskrive hver handling i detalj - vi vil bare angi de viktigste trinnene. Vi har:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f '(x) = (2sin x + 5)' = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Tangentligning:

y = 0 · (x − π /2) + 7 ⇒ y = 7

I sistnevnte tilfelle viste den rette linjen seg å være horisontal, fordi dens vinkelkoeffisient k = 0. Det er ingenting galt med dette - vi snublet bare over et ekstremumpunkt.

En tangent er en rett linje , som berører grafen til funksjonen på ett punkt og alle punktene er i korteste avstand fra grafen til funksjonen. Derfor passerer tangenten tangens til grafen til funksjonen i en viss vinkel, og flere tangenter i forskjellige vinkler kan ikke passere gjennom tangenspunktet. Tangentligninger og normale ligninger til grafen til en funksjon er konstruert ved hjelp av den deriverte.

Tangentligningen er utledet fra linjeligningen .

La oss utlede likningen av tangenten, og deretter likningen av normalen til grafen til funksjonen.

Deretter = kx + 0 = 2. Siden i begge tilfeller .

I han k- vinkelkoeffisient.

Herfra får vi følgende oppføring:

Deretter - Deretter 0 = k(Gitt en funksjon - Gitt en funksjon 0 ) .

Avledet verdi Eksempel 1. "(Gitt en funksjon 0 ) funksjoner Deretter = Eksempel 1.(Gitt en funksjon) på punktet Gitt en funksjon0 er lik skråningen k= tg φ tangent til grafen til en funksjon tegnet gjennom et punkt M0 (Gitt en funksjon 0 , Deretter 0 ) , Hvor Deretter0 = Eksempel 1.(Gitt en funksjon 0 ) . Dette er geometrisk betydning derivat .

Dermed kan vi erstatte k på Eksempel 1. "(Gitt en funksjon 0 ) og få følgende likning av tangenten til grafen til en funksjon :

Deretter - Deretter 0 = Eksempel 1. "(Gitt en funksjon 0 )(Gitt en funksjon - Gitt en funksjon 0 ) .

I problemer som involverer å komponere likningen av en tangent til grafen til en funksjon (og vi vil gå videre til dem snart), er det nødvendig å redusere likningen oppnådd fra formelen ovenfor til ligning av en rett linje i generell form. For å gjøre dette må du flytte alle bokstavene og tallene til venstre side av ligningen, og la null stå på høyre side.

Nå om normalligningen. Normal - dette er en rett linje som går gjennom tangenspunktet til grafen til funksjonen vinkelrett på tangenten. Normal ligning :

(Gitt en funksjon - Gitt en funksjon 0 ) + Eksempel 1. "(Gitt en funksjon 0 )(Deretter - Deretter 0 ) = 0

For å varme opp blir du bedt om å løse det første eksemplet selv, og så se på løsningen. Det er all grunn til å håpe at denne oppgaven ikke blir en «kalddusj» for våre lesere.

Eksempel 0. Lag en tangentligning og en normalligning for grafen til en funksjon i et punkt M (1, 1) .

/ Red. P.Ya. Galperina, N.F. Talyzina. Skriv en tangentligning og en normalligning for grafen til en funksjon , hvis abscissen er tangent .

La oss finne den deriverte av funksjonen:

Nå har vi alt som må erstattes i oppføringen gitt i den teoretiske hjelpen for å få tangentligningen. Vi får

I dette eksemplet var vi heldige: helningen viste seg å være null, så vi reduserer ligningen separat til generelt utseende var ikke nødvendig. Nå kan vi lage normalligningen:

I figuren nedenfor: graf av en funksjon i burgunderfarge, tangent Grønn farge, oransje normal.

Det neste eksemplet er heller ikke komplisert: funksjonen, som i det forrige, er også et polynom, men helningen vil ikke være lik null, så ett trinn til vil bli lagt til - og bringe ligningen til en generell form.

y

Løsning. La oss finne ordinaten til tangentpunktet:

La oss finne den deriverte av funksjonen:

.

La oss finne verdien av den deriverte ved tangenspunktet, det vil si hellingen til tangenten:

Vi erstatter alle de oppnådde dataene i den "blanke formelen" og får tangentligningen:

Vi bringer ligningen til sin generelle form (vi samler alle bokstaver og tall bortsett fra null på venstre side, og lar null på høyre side):

Vi komponerer normalligningen:

+ 1 til grafen til funksjonen Skriv tangenslikningen og normalen til grafen til funksjonen hvis abscissen er tangenspunktet.

Løsning. La oss finne ordinaten til tangentpunktet:

La oss finne den deriverte av funksjonen:

.

La oss finne verdien av den deriverte ved tangenspunktet, det vil si hellingen til tangenten:

.

Vi finner tangentligningen:

Før du bringer ligningen til sin generelle form, må du "gre den" litt: multipliser ledd for ledd med 4. Vi gjør dette og bringer ligningen til sin generelle form:

Vi komponerer normalligningen:

+ 7. Hvis Skriv tangenslikningen og normalen til grafen til funksjonen hvis abscissen er tangenspunktet.

Løsning. La oss finne ordinaten til tangentpunktet:

.

La oss finne den deriverte av funksjonen:

La oss finne verdien av den deriverte ved tangenspunktet, det vil si hellingen til tangenten:

.

Vi får tangentligningen:

Vi bringer ligningen til sin generelle form:

Vi komponerer normalligningen:

En vanlig feil når man skriver tangent- og normalligninger er å ikke legge merke til at funksjonen gitt i eksemplet er kompleks og å beregne dens deriverte som den deriverte av en enkel funksjon. Følgende eksempler er allerede fra komplekse funksjoner(den tilsvarende leksjonen åpnes i et nytt vindu).

Eksempel 5. Skriv tangenslikningen og normalen til grafen til funksjonen hvis abscissen er tangenspunktet.

Løsning. La oss finne ordinaten til tangentpunktet:

Merk følgende! Denne funksjonen er kompleks, siden tangent-argumentet (2 Gitt en funksjon) er i seg selv en funksjon. Derfor finner vi den deriverte av en funksjon som den deriverte av en kompleks funksjon.

Y = f(x) og hvis det på dette punktet kan trekkes en tangent til grafen til funksjonen som ikke er vinkelrett på abscisseaksen, så er vinkelkoeffisienten til tangenten lik f"(a). Vi har allerede brukt dette flere ganger For eksempel, i § 33 ble det slått fast at grafen til funksjonen y = sin x (sinusformet) ved origo danner en vinkel på 45° med x-aksen (mer presist, tangenten til. grafen ved origo gir en vinkel på 45° med den positive retningen til x-aksen), og i eksempel 5 § 33 ble funnet på skjema gitt funksjoner, der tangenten er parallell med x-aksen. I eksempel 2 i § 33 ble det laget en ligning for tangenten til grafen til funksjonen y = x 2 i punktet x = 1 (nærmere bestemt i punktet (1; 1), men oftere er bare abscisseverdien. angitt, og tror at hvis abscisseverdien er kjent, kan ordinatverdien finnes fra ligningen y = f(x)). I denne delen vil vi utvikle en algoritme for å komponere en tangentligning til grafen til enhver funksjon.

La funksjonen y = f(x) og punktet M (a; f(a)) gis, og la det også være kjent at f"(a) eksisterer. La oss lage en likning for tangenten til grafen gitt funksjon på et gitt punkt. Denne ligningen, som ligningen til enhver rett linje som ikke er parallell med ordinataksen, har formen y = kx+m, så oppgaven er å finne verdiene til koeffisientene k og m.

Det er ingen problemer med vinkelkoeffisienten k: vi vet at k = f "(a). For å beregne verdien av m bruker vi det faktum at den ønskede rette linjen går gjennom punktet M(a; f (a)) Dette betyr at hvis vi erstatter koordinatene punktet M i ligningen til den rette linjen, får vi den riktige likheten: f(a) = ka+m, hvorfra vi finner at m = f(a) - ka.
Det gjenstår å erstatte de funnet verdiene av settkoeffisientene inn i ligningen rett:

Vi har fått ligningen for tangenten til grafen til funksjonen y = f(x) i punktet x=a.
Hvis, si,
Ved å erstatte de funnet verdiene a = 1, f(a) = 1 f"(a) = 2 i ligning (1), får vi: y = 1+2(x-f), dvs. y = 2x-1.
Sammenlign dette resultatet med det oppnådd i eksempel 2 fra § 33. Naturligvis skjedde det samme.
La oss lage en ligning for tangenten til grafen til funksjonen y = tan x ved origo. Vi har: dette betyr cos x f"(0) = 1. Ved å erstatte de funnet verdiene a = 0, f(a) = 0, f"(a) = 1 i ligning (1), får vi: y = x.
Derfor tegnet vi tangentoiden i § 15 (se fig. 62) gjennom origo til koordinater i en vinkel på 45° mot abscisseaksen.
Løser disse nok enkle eksempler, vi brukte faktisk en viss algoritme, som finnes i formel (1). La oss gjøre denne algoritmen eksplisitt.

ALGORITMME FOR UTVIKLING AV EN LIGNING FOR EN TANGENT TIL GRAFEN FOR FUNKSJONEN y = f(x)

1) Angi abscissen til tangentpunktet med bokstaven a.
2) Regn ut 1 (a).
3) Finn f"(x) og beregn f"(a).
4) Erstatt de funnet tallene a, f(a), (a) med formel (1).

/ Red. P.Ya. Galperina, N.F. Talyzina. Skriv en ligning for tangenten til grafen til funksjonen i punktet x = 1.
La oss bruke algoritmen, ta i betraktning det i i dette eksemplet

I fig. 126 er en hyperbel avbildet, en rett linje y = 2 er konstruert.
Tegningen bekrefter beregningene ovenfor: den rette linjen y = 2 berører hyperbelen ved punktet (1; 1).

Svar: y = 2- x.
y Tegn en tangent til grafen til funksjonen slik at den er parallell med linjen y = 4x - 5.
La oss avklare problemformuleringen. Kravet om å "tegne en tangent" betyr vanligvis "å danne en ligning for tangenten." Dette er logisk, fordi hvis en person var i stand til å lage en ligning for en tangent, vil han neppe ha problemer med å konstruere en rett linje på koordinatplanet ved å bruke ligningen.
La oss bruke algoritmen for å komponere tangentligningen, og ta i betraktning at i dette eksemplet. Men i motsetning til forrige eksempel er det tvetydighet: abscissen til tangentpunktet er ikke eksplisitt angitt.
La oss begynne å tenke slik. Ønsket tangent må være parallell med den rette linjen y = 4x-5. To linjer er parallelle hvis og bare hvis skråningene deres er like. Dette betyr at vinkelkoeffisienten til tangenten må være lik vinkelkoeffisienten til den gitte rette linjen: Dermed kan vi finne verdien av a fra ligningen f"(a) = 4.
Vi har:
Fra ligningen Dette betyr at det er to tangenter som tilfredsstiller betingelsene for problemet: en i punktet med abscisse 2, den andre i punktet med abscisse -2.
Nå kan du følge algoritmen.

+ 1 til grafen til funksjonen Fra punkt (0; 1) tegner du en tangent til grafen til funksjonen
La oss bruke algoritmen for å komponere tangentligningen, og ta i betraktning at i dette eksemplet, Merk at her, som i eksempel 2, er ikke abscissen til tangentpunktet eksplisitt angitt. Likevel følger vi algoritmen.

Ved betingelse går tangenten gjennom punktet (0; 1). Ved å erstatte verdiene x = 0, y = 1 i ligning (2), får vi:
Som du kan se, i dette eksemplet, klarte vi bare i det fjerde trinnet av algoritmen å finne abscissen til tangentpunktet. Ved å erstatte verdien a =4 i ligning (2), får vi:

I fig. 127 presenterer en geometrisk illustrasjon av det betraktede eksemplet: en graf av funksjonen er plottet

I § ​​32 bemerket vi at for en funksjon y = f(x) som har en derivert i et fast punkt x, er den omtrentlige likheten gyldig:

For å gjøre det lettere for videre resonnement, la oss endre notasjonen: i stedet for x vil vi skrive a, i stedet for vil vi skrive x og følgelig i stedet for vil vi skrive x-a. Da vil den omtrentlige likheten skrevet ovenfor ha formen:

Se nå på fig. 128. En tangent trekkes til grafen til funksjonen y = f(x) i punktet M (a; f (a)). Punktet x er markert på x-aksen nær a. Det er tydelig at f(x) er ordinaten til grafen til funksjonen i spesifisert punkt X. Hva er f(a) + f"(a) (x-a)? Dette er ordinaten til tangenten som tilsvarer det samme punktet x - se formel (1). Hva er meningen med den omtrentlige likheten (3)? Det faktum at For å beregne den omtrentlige verdien av funksjonen, ta ordinatverdien til tangenten.

+ 7. Hvis Finn omtrentlig verdi numerisk uttrykk 1,02 7 .
Det handler om om å finne verdien av funksjonen y = x 7 i punktet x = 1,02. La oss bruke formel (3), og ta hensyn til det i dette eksemplet
Som et resultat får vi:

Hvis vi bruker en kalkulator, får vi: 1,02 7 = 1,148685667...
Som du kan se, er tilnærmingsnøyaktigheten ganske akseptabel.
Svar: 1,02 7 =1,14.

A.G. Mordkovich Algebra 10. klasse

Kalendertematisk planlegging i matematikk, video i matematikk på nett, Matematikk på skolen last ned

Leksjonens innhold leksjonsnotater støttende frame leksjon presentasjon akselerasjon metoder interaktive teknologier Øve på oppgaver og øvelser selvtestverksteder, treninger, case, oppdrag lekser diskusjonsspørsmål retoriske spørsmål fra studenter Illustrasjoner lyd, videoklipp og multimedia fotografier, bilder, grafikk, tabeller, diagrammer, humor, anekdoter, vitser, tegneserier, lignelser, ordtak, kryssord, sitater Tillegg sammendrag artikler triks for nysgjerrige cribs lærebøker grunnleggende og tilleggsordbok med begreper andre Forbedre lærebøker og leksjonerrette feil i læreboka oppdatere et fragment i en lærebok, elementer av innovasjon i leksjonen, erstatte utdatert kunnskap med ny Kun for lærere perfekte leksjoner kalenderplan for året retningslinjer diskusjonsprogrammer Integrerte leksjoner