स्वर्णिम अनुपात किसने बनाया? साहित्य में स्वर्णिम अनुपात

तकनीकी विज्ञान के उम्मीदवार वी. बेल्यानिन, रूसी अनुसंधान केंद्र "कुरचटोव संस्थान" के प्रमुख शोधकर्ता, ई. रोमानोवा, MADI (GTU) के छात्र

विज्ञान और जीवन // चित्रण

स्कूल में स्वर्णिम अनुपात नहीं पढ़ाया जाता। और जब नीचे प्रस्तावित लेख के लेखकों में से एक (तकनीकी विज्ञान के उम्मीदवार वी. बेल्यानिन) ने संस्थान में परीक्षा की तैयारी की प्रक्रिया में, MADI में प्रवेश की योजना बना रहे एक आवेदक के लिए सुनहरे अनुपात के बारे में बात की, तो समस्या अप्रत्याशित रूप से उत्पन्न हो गई गहरी रुचि और बहुत सारे प्रश्न, जिनका उत्तर "मौके पर" दिया गया, कोई उत्तर नहीं मिला। हमने उन्हें एक साथ खोजने का फैसला किया, और फिर सुनहरे अनुपात में सूक्ष्मताओं की खोज की गई जो पहले शोधकर्ताओं को समझ में नहीं आई थी। संयुक्त रचनात्मकता ने ऐसे काम को जन्म दिया जो एक बार फिर युवाओं की रचनात्मक क्षमताओं की पुष्टि करता है और आशा देता है कि विज्ञान की भाषा लुप्त नहीं होगी।

गणित के पैटर्न, जैसे किसी कलाकार के पैटर्न या किसी कवि के पैटर्न, सुंदर होने चाहिए; रंगों या शब्दों जैसे विचारों को सामंजस्यपूर्ण ढंग से जोड़ा जाना चाहिए। सुंदरता पहली कसौटी है: बदसूरत गणित के लिए दुनिया में कोई जगह नहीं है।
जे. एच. हार्डी

सुंदरता गणितीय समस्यायह इसके अंतहीन विकास के लिए सबसे महत्वपूर्ण प्रोत्साहनों में से एक के रूप में कार्य करता है और कई अनुप्रयोगों के निर्माण का कारण बनता है। कभी-कभी दसियों, सैकड़ों और कभी-कभी हजारों वर्ष बीत जाते हैं, लेकिन लोगों को बार-बार एक प्रसिद्ध समाधान और उसकी व्याख्या में अप्रत्याशित मोड़ मिलते हैं। इन दीर्घकालिक और आकर्षक समस्याओं में से एक सुनहरे अनुपात (जीआर) की समस्या बन गई, जो हमारे चारों ओर की दुनिया की कृपा और सद्भाव के तत्वों को दर्शाती है। वैसे, यह याद रखने योग्य है कि यद्यपि अनुपात स्वयं यूक्लिड को ज्ञात था, "सुनहरा अनुपात" शब्द लियोनार्डो दा विंची द्वारा पेश किया गया था (देखें "विज्ञान और जीवन")।

ज्यामितीय रूप से, सुनहरे अनुपात का तात्पर्य एक खंड को दो असमान भागों में विभाजित करना है ताकि बड़ा भाग पूरे खंड और छोटे भाग के बीच औसत आनुपातिक हो (चित्र 1)।

बीजगणितीय रूप से इसे इस प्रकार व्यक्त किया जाता है:

इसके समाधान से पहले भी इस अनुपात के अध्ययन से पता चलता है कि खंडों के बीच एऔर बीकम से कम दो आश्चर्यजनक रिश्ते हैं। उदाहरण के लिए, अनुपात (1) से कोई भी अभिव्यक्ति आसानी से प्राप्त कर सकता है

जो खंडों के बीच अनुपात निर्धारित करता है ए, बी, उनका अंतर और योग। इसलिए, हम सुनहरे अनुपात के बारे में अलग-अलग तरीके से कह सकते हैं: दो खंड सामंजस्यपूर्ण संबंध में हैं यदि उनका अंतर छोटे खंड से संबंधित है क्योंकि बड़ा खंड उनके योग से संबंधित है।

यदि मूल खंड को एक के बराबर लिया जाए तो दूसरा संबंध प्राप्त होता है: ए + बी= 1, जिसका प्रयोग गणित में अक्सर किया जाता है। उस मामले में

ए 2 - बी 2 = ए - बी = अब.

इन परिणामों से खंडों के बीच दो आश्चर्यजनक संबंधों का पता चलता है एऔर बी:

ए 2 - बी 2 = ए - बी = अब,(2)

जिसका उपयोग भविष्य में किया जाएगा।

आइए अब हम अनुपात (1) को हल करने की ओर बढ़ते हैं। व्यवहार में, दो संभावनाओं का उपयोग किया जाता है।

1. आइए संबंध को निरूपित करें ए/बीके माध्यम से। तब हमें समीकरण मिलता है

एक्स 2 - एक्स - 1 = 0, (3)

आमतौर पर केवल सकारात्मक मूल पर ही विचार किया जाता है एक्स 1, एक दिए गए अनुपात में एक खंड का सरल और दृश्य विभाजन दे रहा है। वास्तव में, यदि हम इस मूल के मान का उपयोग करके पूरे खंड को एक मानते हैं एक्स 1, हमें मिलता है ए ≈ 0,618,बी≈ 0,382.

यह सकारात्मक जड़ है एक्ससमीकरण (3) में से 1 को अक्सर कहा जाता है सुनहरा अनुपातया स्वर्णिम अनुपात का अनुपात.किसी खंड का संगत ज्यामितीय विभाजन कहलाता है सुनहरा अनुपात(बिंदु साथचित्र में 1).

आगे की प्रस्तुति की सुविधा के लिए, आइए निरूपित करें एक्स 1 = डी. स्वर्णिम अनुपात के लिए अभी भी कोई आम तौर पर स्वीकृत पदनाम नहीं है। यह स्पष्ट रूप से इस तथ्य के कारण है कि इसे कभी-कभी एक अन्य संख्या के रूप में समझा जाता है, जिसकी चर्चा नीचे की जाएगी।

नकारात्मक जड़ को हमेशा की तरह एक तरफ छोड़ दिया गया एक्स 2 खंड के दो असमान भागों में कम स्पष्ट विभाजन की ओर ले जाता है। मुद्दा यह है कि यह एक विभाजन बिंदु देता है साथ, जो खंड (तथाकथित बाहरी विभाजन) के बाहर स्थित है। वास्तव में, यदि ए + बी= 1, फिर रूट का उपयोग करें एक्स 2, हमें मिलता है ए ≈ -1,618, बी≈ 2.618. इसलिए खंड एनकारात्मक दिशा में रखा जाना चाहिए (चित्र 2)।

2. अनुपात (1) को हल करने का दूसरा विकल्प पहले से मौलिक रूप से भिन्न नहीं है। आइये गिनते हैं अज्ञात संबंध बी/एऔर इसे निरूपित करें य. तब हमें समीकरण मिलता है

य 2 + य -1 = 0 , (4)

जिसकी जड़ें अतार्किक हैं

अगर ए + बी= 1, फिर रूट का उपयोग करें य 1, हमें मिलता है ए = य 1 ≈ 0,618, बी≈ 0.382. जड़ के लिए य 2 हमें मिलता है ए ≈ -1,618, बी≈ 2.618. जड़ों का उपयोग करके सुनहरे अनुपात के अनुपात में एक खंड का ज्यामितीय विभाजन य 1 और य 2 पूरी तरह से पिछले संस्करण के समान है और चित्र से मेल खाता है। 1 और 2.

सकारात्मक जड़ य 1 सीधे समस्या का वांछित समाधान देता है, और कहा भी जाता है सुनहरा अनुपात .

सुविधा के लिए, हम मूल का मान दर्शाते हैं य 1 = डी।

इस प्रकार, साहित्य में, स्वर्णिम अनुपात को गणितीय रूप से संख्या द्वारा व्यक्त किया जाता है डी 1.618 या संख्या डी 0.618, जिनके बीच दो अद्भुत संबंध हैं:

डीडी= 1 और डी - डी = 1. (5)

यह सिद्ध हो चुका है कि संख्याओं का कोई अन्य समान युग्म नहीं है जिसमें ये गुण हों।

सुनहरे अनुपात के लिए दोनों नोटेशन का उपयोग करते हुए, हम समीकरण (3) और (4) के समाधान सममित रूप में लिखते हैं: = डी, = -डी, = डी, = -डी.

सुनहरे अनुपात के असामान्य गुणों का साहित्य में पर्याप्त विस्तार से वर्णन किया गया है। वे इतने अद्भुत हैं कि उन्होंने कई उत्कृष्ट विचारकों के दिमाग को मोहित कर लिया है और उनके चारों ओर रहस्य की आभा पैदा कर दी है।

सुनहरा अनुपात पौधों और खनिजों के विन्यास, ब्रह्मांड के हिस्सों की संरचना और संगीत के पैमाने में पाया जाता है। यह प्रकृति के वैश्विक सिद्धांतों को दर्शाता है, जो जीवित और निर्जीव वस्तुओं के संगठन के सभी स्तरों में व्याप्त है। इसका उपयोग वास्तुकला, मूर्तिकला, चित्रकला, विज्ञान, कंप्यूटर प्रौद्योगिकी और घरेलू वस्तुओं के डिजाइन में किया जाता है। सुनहरे अनुपात का विन्यास लेकर चलने वाली रचनाएँ आनुपातिक और सुसंगत दिखाई देती हैं, हमेशा आँख को भाती हैं, और गणितीय भाषासुनहरा अनुपात भी कम सुंदर और सुरुचिपूर्ण नहीं है।

संबंध (2) से समानता (5) के अलावा, हम तीन दिलचस्प संबंधों को अलग कर सकते हैं जिनमें एक निश्चित पूर्णता है और जो काफी आकर्षक और सौंदर्यपूर्ण रूप से प्रसन्न दिखते हैं:

(6)

उदाहरण के लिए, प्रकृति की भव्यता और गहराई को न केवल सितारों या पर्वत चोटियों पर विचार करते समय महसूस किया जा सकता है, बल्कि कुछ अद्भुत सूत्रों को देखकर भी महसूस किया जा सकता है, जिनकी सुंदरता के लिए गणितज्ञों द्वारा बहुत सराहना की जाती है। इनमें सुनहरे अनुपात के खूबसूरत रिश्ते, शानदार यूलर फॉर्मूला शामिल हैं ई iπ = -1 (कहां मैं= √-1), प्रसिद्ध नेपियर संख्या (प्राकृतिक लघुगणक का आधार) को परिभाषित करने वाला सूत्र: e = lim(1 + 1/ एन) एन = 2.718 बजे एन→ ∞, और कई अन्य।

अनुपात (1) को हल करने के बाद, इसका विचार काफी सरल लगता है, लेकिन, जैसा कि अक्सर कई लोगों के साथ होता है, पहली नज़र में सरल कार्य, इसमें कई बारीकियां छुपी हुई हैं। इन उल्लेखनीय सूक्ष्मताओं में से एक, जिसे शोधकर्ताओं ने अब तक नजरअंदाज किया है, वह है समीकरण (3) और (4) की जड़ों के बीच तीन उल्लेखनीय त्रिभुजों के कोणों के बीच संबंध।

इसे देखने के लिए, विचार करें कि सुनहरे अनुपात के अनुपात में विभाजित एक-आयामी रेखा खंड को आसानी से त्रिकोण के रूप में दो-आयामी छवि में कैसे बदला जा सकता है। ऐसा करने के लिए, पहले चित्र का उपयोग करें। 1, खंड पर एक तरफ रख दें अबखंड की लंबाई एदो बार - बिंदु से एबिंदु की ओर मेंऔर, इसके विपरीत, बिंदु से मेंतरफ के लिए ए. हमें दो अंक मिलते हैं साथ 1 और साथ 2 खंड को विभाजित करना अबसुनहरे खंड के अनुपात में विभिन्न सिरों से (चित्र 3)। बराबर खंडों की गिनती ए.सी 1 और सूरज 2 त्रिज्या, और अंक एऔर मेंवृत्तों के केंद्र पर, दो चाप तब तक खींचिए जब तक वे शीर्ष बिंदु पर प्रतिच्छेद न कर दें साथ. बिंदुओं को जोड़ना एऔर साथ, और भी मेंऔर साथ,हमें एक समद्विबाहु त्रिभुज मिलता है एबीसीपार्टियों के साथ अब = ए + बी = 1, ए.सी = = सूरज = ए = डी≈ 0.618. शीर्षों पर कोणों का आकार एऔर मेंआइए हम शीर्ष पर α को निरूपित करें साथ- β. आइए इन कोणों की गणना करें।

कोसाइन प्रमेय द्वारा

(अब) 2 = 2(ए.सी) 2 (1 - कॉस β)।

खंडों के संख्यात्मक मानों को प्रतिस्थापित करना अबऔर ए.सीइस सूत्र में, हम पाते हैं

वैसे ही हम पाते हैं

(8)

द्वि-आयामी छवि में सुनहरे अनुपात के उद्भव ने समीकरणों (3) और (4) की जड़ों को त्रिभुज के कोणों से जोड़ना संभव बना दिया एबीसी, जिसे कहा जा सकता है स्वर्णिम अनुपात का पहला त्रिकोण.

आइए चित्र का उपयोग करके एक समान निर्माण करें। 2. यदि खंड की निरंतरता पर अबबिंदु से स्थगित मेंदाईं ओर खंड के आकार के बराबर एक खंड है ए, और केंद्रों के चारों ओर घूमें एऔर मेंदोनों खंडों को त्रिज्या के रूप में तब तक ऊपर उठाएं जब तक वे स्पर्श न कर लें, हमें मिलता है दूसरा त्रिकोण सुनहरा अनुपात(चित्र 4) . इस समद्विबाहु त्रिभुज में, भुजा अब = ए + बी= 1, पक्ष ए.सी = सूरज = डी≈1.618, और इसलिए, कोसाइन प्रमेय के सूत्र का उपयोग करके, हम प्राप्त करते हैं

(9)

शीर्ष पर कोण a साथ 36° के बराबर है और संबंध (8) द्वारा स्वर्णिम अनुपात से संबंधित है। पिछले मामले की तरह, इस त्रिभुज के कोण समीकरण (3) और (4) की जड़ों से संबंधित हैं।

सुनहरे अनुपात का दूसरा त्रिकोण एक नियमित उत्तल पेंटागन के मुख्य घटक तत्व के रूप में कार्य करता है और एक नियमित तारकीय पेंटागन (पेंटाग्राम) के अनुपात को निर्धारित करता है, जिसके गुणों पर पुस्तक में विस्तार से चर्चा की गई है।

एक तारे के आकार का पंचकोण एक सममित आकृति है, और साथ ही, इसके खंडों के संबंधों में असममित सुनहरा अनुपात दिखाई देता है। विरोधों का ऐसा संयोजन हमेशा अपनी गहरी एकता से आकर्षित करता है, जिसका ज्ञान व्यक्ति को प्रकृति के छिपे हुए नियमों में प्रवेश करने और उनकी असाधारण गहराई और सद्भाव को समझने की अनुमति देता है। तारे के आकार के पंचकोण में खंडों की संगति से मोहित होकर पाइथागोरस ने इसे अपने वैज्ञानिक समुदाय के प्रतीक के रूप में चुना।

खगोलशास्त्री आई. केपलर (XVII सदी) के समय से, कभी-कभी अधिक मौलिक क्या है - पाइथागोरस प्रमेय या स्वर्णिम अनुपात के बारे में अलग-अलग दृष्टिकोण व्यक्त किए गए हैं। पाइथागोरस प्रमेय गणित की नींव पर आधारित है, यह इसकी आधारशिलाओं में से एक है। सुनहरा अनुपातब्रह्मांड की सद्भावना और सुंदरता के आधार पर निहित है। पहली नज़र में, इसे समझना मुश्किल नहीं है और इसमें महत्वपूर्ण संपूर्णता नहीं है। हालाँकि, इसके कुछ अप्रत्याशित और गहन गुणों को हाल ही में महसूस किया गया है, जो इसकी छिपी सूक्ष्मता और संभावित बहुमुखी प्रतिभा का सम्मान करने की आवश्यकता का सुझाव देता है। पाइथागोरस प्रमेय और उनके विकास में स्वर्णिम अनुपात एक दूसरे के साथ और ज्यामितीय और बीजगणितीय गुणों के साथ घनिष्ठ रूप से जुड़े हुए हैं। उनके बीच कोई अंतर या बुनियादी अंतर नहीं है। वे प्रतिस्पर्धा नहीं करते, उनके अलग-अलग उद्देश्य हैं।

यह बहुत संभव है कि दोनों दृष्टिकोण समान हों, क्योंकि एक समकोण त्रिभुज है जिसमें सुनहरे अनुपात की विभिन्न विशेषताएं शामिल हैं। दूसरे शब्दों में, एक ज्यामितीय आकृति है जो पूरी तरह से दो अद्भुत गणितीय तथ्यों को जोड़ती है - पाइथागोरस प्रमेय और सुनहरा अनुपात।

ऐसे त्रिभुज के निर्माण के लिए भुजा को फैलाना ही पर्याप्त है सूरजत्रिकोण एबीसी(चित्र 4) बिंदु पर चौराहे तक ईबिंदु पर लंबवत् बहाल होने के साथ एतरफ के लिए अब(चित्र 5)।

एक आंतरिक समद्विबाहु त्रिभुज में ऐसकोण φ (कोण ऐस) 144° के बराबर है, और कोण ψ (कोण पूर्वी वायु कमानऔर एईएस) 18 o के बराबर है। ओर ए.सी = से = पूर्वोत्तर = डी. पाइथागोरस प्रमेय का उपयोग करके, यह पता लगाना आसान है कि पैर की लंबाई कितनी है

इस परिणाम का उपयोग करके हम आसानी से संबंध पर पहुंच जाते हैं

तो जड़ का सीधा कनेक्शन मिल गया है य 2 समीकरण (4) - समीकरण (3) और (4) के मूलों में से अंतिम - 144 o के कोण के साथ। इस संबंध में, त्रिकोण ऐसबुलाया जा सकता है स्वर्णिम अनुपात का तीसरा त्रिकोण.

यदि एक अद्भुत समकोण त्रिभुज में एवेन्यूकोण का समद्विभाजक खींचिए कैबजब तक यह किनारे से न कट जाए ई.वीबिंदु पर एफ, फिर हम उसे किनारे से देखेंगे अबचार कोण हैं: 36 o, 72 o, 108 o और 144 o, जिनके साथ स्वर्णिम अनुपात समीकरणों की जड़ें सीधे संबंधित हैं (संबंध (7) - (10))। इस प्रकार, प्रस्तुत समकोण त्रिभुज में समबाहु त्रिभुजों की पूरी आकाशगंगा शामिल है जिसमें सुनहरे अनुपात की विशेषताएं हैं। इसके अलावा, यह काफी उल्लेखनीय है कि कर्ण पर कोई भी दो खंड हैं यूरोपीय संघ= डीऔर सीएफ़= 1.0 के साथ स्वर्णिम अनुपात के संबंध में हैं एफ = डी. कोण ψ जड़ों से संबंधित है डीऔर डीसंबंधों द्वारा समीकरण (3) और (4)।

ऊपर प्रस्तुत समद्विबाहु त्रिभुजों की रचनाएँ, जिनके कोण सुनहरे अनुपात के समीकरणों की जड़ों से जुड़े हुए हैं, मूल खंड पर आधारित हैं अबऔर उसके हिस्से एऔर बी. हालाँकि, सुनहरा अनुपात आपको न केवल ऊपर वर्णित त्रिकोणों को मॉडल करने की अनुमति देता है, बल्कि विभिन्न अन्य ज्यामितीय आकृतियों को भी प्रदर्शित करता है जो सामंजस्यपूर्ण संबंधों के तत्वों को ले जाते हैं।

आइए हम ऐसे निर्माणों के दो उदाहरण दें। सबसे पहले, खंड पर विचार करें अब, चित्र में प्रस्तुत किया गया है। 1. बात बताइये साथ- वृत्त का केंद्र, खंड बी- त्रिज्या। आइए एक त्रिज्या बनाएं बीएक बिंदु से वृत्त और उस पर स्पर्श रेखाएँ ए(चित्र 6)। आइए स्पर्शरेखा बिंदुओं को जोड़ें ईऔर एफएक बिंदु के साथ साथ. परिणाम एक असममित समचतुर्भुज है एईसीएफ, जिसमें विकर्ण ए.सीइसे दो समान समकोण त्रिभुजों में विभाजित करता है ऐसऔर एसीएफ़.

आइए उनमें से एक पर करीब से ध्यान दें, उदाहरण के लिए, एक त्रिकोण ऐस. इस त्रिभुज में कोण एईएस- सीधी रेखा, कर्ण ए.सी = ए, टांग से = बीऔर पैर ऐ = √अब≈ 0.486, जो संबंध (2) से अनुसरण करता है। इसलिए, पैर ऐखंडों के बीच ज्यामितीय माध्य (आनुपातिक) है एऔर बी, अर्थात्, संख्याओं के बीच समरूपता के ज्यामितीय केंद्र को व्यक्त करता है ए≈ 0.618 और बी ≈ 0,382.

आइए इस त्रिभुज के कोण ज्ञात करें:

पिछले मामलों की तरह, कोण δ और ε कोसाइन के माध्यम से समीकरण (3) और (4) की जड़ों से संबंधित हैं।

ध्यान दें कि एक असममित समचतुर्भुज एक समचतुर्भुज के समान है एईसीएफ, बिंदु से स्पर्शरेखा खींचकर प्राप्त किया जाता है मेंत्रिज्या के एक वृत्त के लिए एऔर बिंदु पर केंद्रित है ए.

असममित समचतुर्भुज एईसीएफजीवित प्रकृति में गठन और विकास की घटनाओं का विश्लेषण करते समय पुस्तक में एक अलग तरीके से प्राप्त किया गया। सही त्रिकोण एईएसइस कार्य में इसे "जीवित" त्रिभुज कहा गया है, क्योंकि यह प्रकृति के विभिन्न संरचनात्मक तत्वों के अनुरूप दृश्य छवियां उत्पन्न करने में सक्षम है, और कुछ जीवित जीवों के विकास की शुरुआत के ज्यामितीय आरेखों के निर्माण में कुंजी के रूप में कार्य करता है।

दूसरा उदाहरण सुनहरे अनुपात के पहले और तीसरे त्रिकोण से संबंधित है। सुनहरे अनुपात के पहले दो समान त्रिभुजों से हम 72° और 108° के आंतरिक कोणों वाला एक समचतुर्भुज बनाते हैं। इसी प्रकार, हम सुनहरे अनुपात के दो समान तीसरे त्रिभुजों को 36° और 144° के आंतरिक कोणों के साथ एक समचतुर्भुज में जोड़ते हैं। यदि इन समचतुर्भुजों की भुजाएँ एक-दूसरे के बराबर हों, तो वे शून्य या अतिव्यापन के बिना एक अनंत तल को भर सकते हैं। विमान को भरने के लिए संबंधित एल्गोरिदम बीसवीं सदी के 70 के दशक के अंत में ऑक्सफोर्ड विश्वविद्यालय के सैद्धांतिक भौतिक विज्ञानी आर. पेनरोज़ द्वारा विकसित किया गया था। इसके अलावा, यह पता चला कि परिणामी मोज़ेक में प्रत्येक प्रकार के rhombuses की पूर्णांक संख्या के साथ एक प्राथमिक सेल का चयन करना असंभव है, जिसके अनुवाद से संपूर्ण मोज़ेक प्राप्त करना संभव हो जाएगा। लेकिन सबसे उल्लेखनीय बात यह थी कि अनंत पेनरोज़ मोज़ेक में "संकीर्ण" समचतुर्भुजों की संख्या और "चौड़े" समचतुर्भुजों की संख्या का अनुपात बिल्कुल सुनहरे अनुपात के मान के बराबर है। डी = 0,61803...!

इस उदाहरण में, कोणों के माध्यम से व्यक्त किए गए सुनहरे अनुपात की सभी जड़ें आश्चर्यजनक रूप से दो प्राथमिक आकृतियों - रोम्बस के साथ एक अनंत विमान के गैर-तुच्छ भरने के मामलों में से एक के साथ संयुक्त हैं।

निष्कर्ष में, हम ध्यान दें कि स्वर्णिम अनुपात समीकरणों की जड़ों और त्रिभुजों के कोणों के बीच संबंध के ऊपर दिए गए विभिन्न उदाहरण इस तथ्य को दर्शाते हैं कि स्वर्णिम अनुपात पहले की तुलना में अधिक व्यापक समस्या है। यदि पहले सुनहरे अनुपात के अनुप्रयोग का क्षेत्र अंततः खंडों के अनुपात और इसकी जड़ों (फाइबोनैचि संख्या) के संख्यात्मक मूल्यों से जुड़े विभिन्न अनुक्रमों को माना जाता था, तो अब यह पता चला है कि सुनहरा अनुपात विभिन्न प्रकार उत्पन्न कर सकता है ज्यामितीय वस्तुओं और समीकरणों की जड़ों में एक स्पष्ट त्रिकोणमितीय अभिव्यक्ति होती है।

लेखक इस बात से अवगत हैं कि सुनहरे अनुपात से जुड़े गणितीय संबंधों की सुंदरता के संबंध में ऊपर व्यक्त दृष्टिकोण व्यक्तिगत सौंदर्य अनुभवों को दर्शाता है। आधुनिक दार्शनिक साहित्य में, सौंदर्यशास्त्र और सुंदरता की अवधारणाओं की व्याख्या काफी व्यापक रूप से की जाती है और इसका उपयोग सहज स्तर पर किया जाता है। ये अवधारणाएँ मुख्यतः कला से संबंधित हैं। सौंदर्य की दृष्टि से वैज्ञानिक रचनात्मकता की सामग्री पर व्यावहारिक रूप से साहित्य में विचार नहीं किया जाता है। सौंदर्य मापदंडों के पहले सन्निकटन के रूप में वैज्ञानिक अनुसंधानहम उनकी तुलनात्मक सादगी, उनकी अंतर्निहित समरूपता और दृश्य छवियां उत्पन्न करने की क्षमता को श्रेय दे सकते हैं। इन सभी सौंदर्य मानकों को "सुनहरा अनुपात" नामक कार्य द्वारा पूरा किया जाता है। सामान्य तौर पर, विज्ञान में सौंदर्यशास्त्र की समस्याएं हल होने से बहुत दूर हैं, हालांकि वे बहुत रुचि रखते हैं।

यह सहज रूप से महसूस किया जाता है कि सुनहरा अनुपात अभी भी अपने रहस्य छुपाता है। उनमें से कुछ, संभवतः, सतह पर पड़े हैं, अपने नए शोधकर्ताओं की असामान्य नज़र की प्रतीक्षा कर रहे हैं। सुनहरे अनुपात के गुणों का ज्ञान रचनात्मक लोगों के लिए एक अच्छी नींव के रूप में काम कर सकता है, जिससे उन्हें आत्मविश्वास मिलता हैविज्ञान और में.

ज़िंदगी

साहित्य 1. शेवेलेव आई. श., मारुतेव आई. ए., श्मेलेव आई. पी.स्वर्णिम अनुपात: सद्भाव की प्रकृति पर तीन विचार।

- एम.: स्ट्रॉइज़दैट, 1990. - 343 पी। 2. स्टाखोव ए.पी.स्वर्णिम अनुपात कोड.

- एम.: रेडियो और संचार, 1984. - 152 पी। 3. वासुतिन्स्की एन.ए.सुनहरा अनुपात.

- एम.: यंग गार्ड, 1990. - 238 पी। 4. कोरोब्को वी.आई.स्वर्णिम अनुपात: सद्भाव के कुछ दार्शनिक पहलू।

- एम. - ओरेल: 2000. - 204 पी। 5. उर्मेंटसेव यू.सुनहरा अनुपात

// प्रकृति, 1968, संख्या 11। 6. पोपकोव वी.वी., शिपित्सिन ई.वी.कार्नोट चक्र में स्वर्णिम अनुपात

// यूएफएन, 2000, खंड 170, संख्या 11। 7. कॉन्स्टेंटिनोव आई.डोडेकाहेड्रोन के साथ कल्पनाएँ

// विज्ञान और जीवन, 2001, संख्या 2। 8. शेवलेव आई. श्री.ज्यामितीय सामंजस्य

// विज्ञान और जीवन, 1965, संख्या 8। 9. गार्डनर एम.पेनरोज़ टाइलिंग से लेकर मजबूत सिफर तक

एक व्यक्ति अपने आस-पास की वस्तुओं को उनके आकार के आधार पर अलग करता है। किसी वस्तु के आकार में रुचि महत्वपूर्ण आवश्यकता से निर्धारित हो सकती है, या यह आकार की सुंदरता के कारण हो सकती है। यह रूप, जो समरूपता और सुनहरे अनुपात के संयोजन पर आधारित है, सर्वोत्तम दृश्य धारणा और सौंदर्य और सद्भाव की भावना की उपस्थिति को बढ़ावा देता है। संपूर्ण हमेशा भागों से बना होता है, विभिन्न आकारों के हिस्से एक-दूसरे से और संपूर्ण से एक निश्चित संबंध में होते हैं। स्वर्णिम अनुपात का सिद्धांत कला, विज्ञान, प्रौद्योगिकी और प्रकृति में संपूर्ण और उसके भागों की संरचनात्मक और कार्यात्मक पूर्णता की उच्चतम अभिव्यक्ति है।

स्वर्णिम अनुपात - हार्मोनिक अनुपात

गणित में अनुपात(अव्य. अनुपात)दो संबंधों की समानता को बुलाओ:

ए : बी = सी : डी.

सीधा खंड अबनिम्नलिखित प्रकार से दो भागों में विभाजित किया जा सकता है:

दो बराबर भागों में - अब : ए.सी. = अब : ईसा पूर्व;
किसी भी दृष्टि से दो असमान भागों में (ऐसे भाग अनुपात नहीं बनाते);
इस प्रकार, जब अब : ए.सी. = ए.सी. : ईसा पूर्व.

उत्तरार्द्ध चरम और औसत अनुपात में एक खंड का स्वर्णिम विभाजन या विभाजन है।

स्वर्णिम अनुपात एक खंड का असमान भागों में ऐसा आनुपातिक विभाजन है, जिसमें संपूर्ण खंड बड़े भाग से संबंधित होता है जैसे कि बड़ा भाग स्वयं छोटे से संबंधित होता है; या दूसरे शब्दों में, छोटा खंड बड़े के लिए है, क्योंकि बड़ा संपूर्ण के लिए है:

ए : बी = बी : सी
या
सी : बी = बी : ए.

चावल। 1.स्वर्णिम अनुपात की ज्यामितीय छवि

सुनहरे अनुपात के साथ व्यावहारिक परिचय एक कंपास और रूलर का उपयोग करके एक सीधी रेखा खंड को सुनहरे अनुपात में विभाजित करने से शुरू होता है।

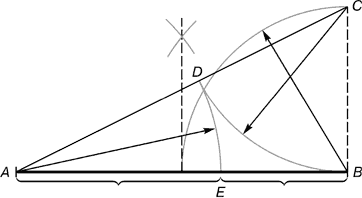
चावल। 2.ईसा पूर्व = 1/2 अब; सीडी = ईसा पूर्व

बिंदु से बीआधे के बराबर एक लंब बहाल किया जाता है अब. अंक प्राप्त हुआ सीएक रेखा द्वारा एक बिंदु से जुड़ा हुआ ए. परिणामी रेखा पर एक खंड अंकित किया गया है ईसा पूर्वएक बिंदु के साथ समाप्त होना डी. खंड विज्ञापनप्रत्यक्ष में स्थानांतरित कर दिया गया अब. परिणामी बिंदु ईएक खंड को विभाजित करता है अबस्वर्णिम अनुपात अनुपात में.

स्वर्णिम अनुपात के खंडों को अनंत अपरिमेय अंश के रूप में व्यक्त किया जाता है ए.ई.= 0.618..., यदि अबएक के रूप में ले लो होना= 0.382... व्यावहारिक उद्देश्यों के लिए, 0.62 और 0.38 के अनुमानित मान अक्सर उपयोग किए जाते हैं। यदि खंड अब 100 भागों के रूप में लिया जाए, तो खंड का बड़ा भाग 62 भागों के बराबर है, और छोटा भाग 38 भागों के बराबर है।

सुनहरे अनुपात के गुणों को समीकरण द्वारा वर्णित किया गया है:

एक्स 2 – एक्स – 1 = 0.

इस समीकरण का हल:

सुनहरे अनुपात के गुणों ने इस संख्या के चारों ओर रहस्य और लगभग रहस्यमय पूजा की एक रोमांटिक आभा पैदा कर दी है।

दूसरा स्वर्णिम अनुपात

बल्गेरियाई पत्रिका "फादरलैंड" (नंबर 10, 1983) ने स्वेतन त्सेकोव-करंदश का एक लेख "दूसरे सुनहरे खंड पर" प्रकाशित किया, जो मुख्य खंड से आता है और 44:56 का एक और अनुपात देता है।

यह अनुपात वास्तुकला में पाया जाता है, और लम्बी क्षैतिज प्रारूप की छवियों की रचनाओं का निर्माण करते समय भी होता है।

चावल। 3.

विभाजन निम्नानुसार किया जाता है। खंड अबस्वर्णिम अनुपात के अनुसार विभाजित। बिंदु से सीलम्बवत बहाल है सीडी. RADIUS अबएक बात है डी, जो एक रेखा द्वारा एक बिंदु से जुड़ा होता है ए. समकोण एसीडीआधे में विभाजित है. बिंदु से सीएक रेखा तब तक खींची जाती है जब तक वह रेखा के साथ प्रतिच्छेद न कर दे विज्ञापन. डॉट ईएक खंड को विभाजित करता है विज्ञापन 56:44 के संबंध में।

चावल। 4.

यह चित्र दूसरे स्वर्णिम अनुपात की रेखा की स्थिति दर्शाता है। यह स्वर्ण अनुपात रेखा और आयत की मध्य रेखा के बीच में स्थित है।

स्वर्ण त्रिभुज

आरोही और अवरोही श्रृंखला के सुनहरे अनुपात के खंड खोजने के लिए, आप इसका उपयोग कर सकते हैं पेंटाग्राम.

चावल। 5.एक नियमित पंचकोण और पंचग्राम का निर्माण

पेंटाग्राम बनाने के लिए, आपको एक नियमित पेंटागन बनाने की आवश्यकता है। इसके निर्माण की विधि जर्मन चित्रकार और ग्राफिक कलाकार अल्ब्रेक्ट ड्यूरर (1471...1528) द्वारा विकसित की गई थी। होने देना हे- वृत्त का केंद्र, ए– एक वृत्त पर एक बिंदु और ई– खंड के मध्य ओ.ए.. त्रिज्या के लंबवत ओ.ए., बिंदु पर बहाल किया गया हे, वृत्त को बिंदु पर प्रतिच्छेद करता है डी. कम्पास का उपयोग करके, व्यास पर एक खंड आलेखित करें सी.ई. = ईडी. एक वृत्त में अंकित एक नियमित पंचभुज की भुजा की लंबाई है डीसी. वृत्त पर खंड बिछाएँ डीसीऔर हमें एक नियमित पंचभुज बनाने के लिए पांच अंक मिलते हैं। हम पेंटागन के कोनों को विकर्णों के माध्यम से एक दूसरे से जोड़ते हैं और एक पेंटाग्राम प्राप्त करते हैं। पंचभुज के सभी विकर्ण एक दूसरे को सुनहरे अनुपात से जुड़े खंडों में विभाजित करते हैं।

पंचकोणीय तारे का प्रत्येक सिरा एक स्वर्ण त्रिभुज का प्रतिनिधित्व करता है। इसकी भुजाएं शीर्ष पर 36° का कोण बनाती हैं और किनारे पर रखा आधार इसे सुनहरे अनुपात के अनुपात में विभाजित करता है।

चावल। 6.स्वर्ण त्रिभुज का निर्माण

हम एक प्रत्यक्ष कार्य करते हैं अब. बिंदु से एउस पर एक खंड तीन बार रखें हेपरिणामी बिंदु के माध्यम से मनमाना मूल्य पीरेखा पर एक लंब खींचिए अब, बिंदु के दाएं और बाएं लंबवत पर पीखंडों को अलग रखें हे. अंक प्राप्त हुए डीऔर डी 1 एक बिंदु से सीधी रेखाओं से जुड़ें ए. खंड डीडीलाइन पर 1 लगाएं विज्ञापन 1, एक अंक प्राप्त करना सी. उसने लाइन बांट दी विज्ञापनस्वर्णिम अनुपात के अनुपात में 1. पंक्तियां विज्ञापन 1 और डीडी 1 का उपयोग "सुनहरा" आयत बनाने के लिए किया जाता है।

स्वर्णिम अनुपात का इतिहास

यह आम तौर पर स्वीकार किया जाता है कि स्वर्णिम विभाजन की अवधारणा को प्राचीन यूनानी दार्शनिक और गणितज्ञ (छठी शताब्दी ईसा पूर्व) पाइथागोरस द्वारा वैज्ञानिक उपयोग में लाया गया था। ऐसी धारणा है कि पाइथागोरस ने स्वर्णिम विभाजन का अपना ज्ञान मिस्रियों और बेबीलोनियों से उधार लिया था। दरअसल, चेप्स पिरामिड, मंदिर, बेस-रिलीफ, घरेलू सामान और कब्र से सजावट के अनुपात से संकेत मिलता है कि मिस्र के कारीगरों ने उन्हें बनाते समय सुनहरे विभाजन के अनुपात का उपयोग किया था। फ्रांसीसी वास्तुकार ले कोर्बुसीयर ने पाया कि एबिडोस में फिरौन सेती प्रथम के मंदिर की राहत और फिरौन रामसेस को चित्रित करने वाली राहत में, आंकड़ों का अनुपात स्वर्ण प्रभाग के मूल्यों के अनुरूप है। वास्तुकार खेसीरा को उनके नाम पर बने मकबरे के एक लकड़ी के बोर्ड की राहत पर चित्रित किया गया है, उनके हाथों में मापने के उपकरण हैं जिनमें सुनहरे विभाजन के अनुपात दर्ज किए गए हैं।

यूनानी कुशल ज्यामितिक थे। उन्होंने ज्यामितीय आकृतियों का उपयोग करके अपने बच्चों को अंकगणित भी सिखाया। पाइथागोरस वर्ग और इस वर्ग का विकर्ण गतिशील आयतों के निर्माण का आधार थे।

चावल। 7.गतिशील आयतें

प्लेटो (427...347 ईसा पूर्व) को भी स्वर्णिम विभाजन का ज्ञान था। उनका संवाद "टाइमियस" पायथागॉरियन स्कूल के गणितीय और सौंदर्य संबंधी विचारों और विशेष रूप से स्वर्णिम प्रभाग के मुद्दों के लिए समर्पित है।

पार्थेनन के प्राचीन यूनानी मंदिर के अग्रभाग में सुनहरे अनुपात हैं। इसकी खुदाई के दौरान, कम्पास की खोज की गई थी जिसका उपयोग प्राचीन दुनिया के वास्तुकारों और मूर्तिकारों द्वारा किया जाता था। पोम्पियन कम्पास (नेपल्स में संग्रहालय) में भी स्वर्ण मंडल का अनुपात शामिल है।

चावल। 8.

प्राचीन साहित्य में जो हमारे सामने आया है, स्वर्णिम विभाजन का उल्लेख सबसे पहले यूक्लिड के तत्वों में किया गया था। एलिमेंट्स की दूसरी पुस्तक में, स्वर्ण मंडल का एक ज्यामितीय निर्माण दिया गया है। यूक्लिड के बाद, स्वर्ण विभाजन का अध्ययन हाइप्सिकल्स (द्वितीय शताब्दी ईसा पूर्व), पप्पस (तृतीय शताब्दी ईस्वी) और अन्य द्वारा किया गया था। मध्ययुगीन यूरोपके माध्यम से हम स्वर्णिम प्रभाग से परिचित हुए अरबी अनुवादयूक्लिड की "शुरुआत"। नवरे (तृतीय शताब्दी) के अनुवादक जे. कैम्पानो ने अनुवाद पर टिप्पणियाँ कीं। स्वर्ण मंडल के रहस्यों को ईर्ष्यापूर्वक संरक्षित किया गया और सख्त गोपनीयता में रखा गया। वे केवल दीक्षार्थियों के लिए ही जाने जाते थे।

पुनर्जागरण के दौरान, ज्यामिति और कला दोनों में, विशेष रूप से वास्तुकला में इसके उपयोग के कारण वैज्ञानिकों और कलाकारों के बीच स्वर्ण प्रभाग में रुचि बढ़ गई, एक कलाकार और वैज्ञानिक लियोनार्डो दा विंची ने देखा कि इतालवी कलाकारों के पास बहुत अनुभवजन्य अनुभव था, लेकिन बहुत कम ज्ञान । उन्होंने कल्पना की और ज्यामिति पर एक किताब लिखना शुरू किया, लेकिन उसी समय भिक्षु लुका पैसिओली की एक किताब सामने आई और लियोनार्डो ने अपना विचार त्याग दिया। समकालीनों और विज्ञान के इतिहासकारों के अनुसार, लुका पैसिओली एक वास्तविक ज्योतिषी थे, जो फाइबोनैचि और गैलीलियो के बीच की अवधि में इटली के सबसे महान गणितज्ञ थे। लुका पैसिओली चित्रकार पिएरो डेला फ्रांसेची के छात्र थे, जिन्होंने दो किताबें लिखीं, जिनमें से एक का शीर्षक ऑन पर्सपेक्टिव इन पेंटिंग था। उन्हें वर्णनात्मक ज्यामिति का निर्माता माना जाता है।

लुका पैसिओली कला के लिए विज्ञान के महत्व को भली-भांति समझते थे। 1496 में, ड्यूक मोरो के निमंत्रण पर, वह मिलान आये, जहाँ उन्होंने गणित पर व्याख्यान दिया। लियोनार्डो दा विंची ने उस समय मिलान में मोरो कोर्ट में भी काम किया था। 1509 में, लुका पैसिओली की पुस्तक "द डिवाइन प्रोपोर्शन" शानदार ढंग से निष्पादित चित्रों के साथ वेनिस में प्रकाशित हुई थी, यही कारण है कि यह माना जाता है कि वे लियोनार्डो दा विंची द्वारा बनाए गए थे। यह पुस्तक सुनहरे अनुपात का एक उत्साही भजन थी। सुनहरे अनुपात के कई फायदों के बीच, भिक्षु लुका पैसिओली इसके "दिव्य सार" को दिव्य त्रिमूर्ति की अभिव्यक्ति के रूप में नामित करने से नहीं चूके - ईश्वर पिता, ईश्वर पुत्र और ईश्वर पवित्र आत्मा (यह निहित था कि छोटा) खंड ईश्वर पुत्र का अवतार है, बड़ा खंड ईश्वर पिता है, और संपूर्ण खंड - ईश्वर पवित्र आत्मा है)।

ई-पुस्तकें:

मारियो लिवियो.

04/18/2011 ए. एफ. अफानसयेव अद्यतन 06/16/12

प्लास्टिक कला के किसी भी कार्य की कलात्मक छवि की खोज में आयाम और अनुपात मुख्य कार्यों में से एक हैं। यह स्पष्ट है कि आकार का मुद्दा उस कमरे को ध्यान में रखते हुए तय किया जाता है जहां यह स्थित होगा और इसके आसपास की वस्तुएं।

अनुपात (आयामी मूल्यों के अनुपात) के बारे में बोलते हुए, हम उन्हें एक फ्लैट छवि (पेंटिंग, मार्क्वेट्री) के प्रारूप में, एक वॉल्यूमेट्रिक ऑब्जेक्ट के समग्र आयामों (लंबाई, ऊंचाई, चौड़ाई) के अनुपात में ध्यान में रखते हैं। एक समूह की दो वस्तुएँ ऊंचाई या लंबाई में भिन्न होती हैं, एक ही वस्तु के दो स्पष्ट रूप से दिखाई देने वाले भागों के आकार के अनुपात में, आदि।

कई शताब्दियों से ललित कला के क्लासिक्स में, अनुपात बनाने की एक तकनीक का पता लगाया गया है, जिसे गोल्डन सेक्शन या गोल्डन नंबर कहा जाता है (यह शब्द लियोनार्डो दा विंची द्वारा पेश किया गया था)। स्वर्णिम अनुपात, या गतिशील समरूपता का सिद्धांत यह है कि "एक पूर्ण के दो भागों के बीच का अनुपात उसके बड़े भाग और संपूर्ण के अनुपात के बराबर होता है" (या, तदनुसार, संपूर्ण और बड़े भाग के अनुपात के बराबर होता है)। गणितीय रूप से यह है

संख्या को - 1 ± 2?5 के रूप में व्यक्त किया जाता है - जो 1.6180339... या 0.6180339... देता है। कला में, 1.62 को स्वर्णिम संख्या के रूप में लिया जाता है, यानी कि इसके छोटे के अनुपात में बड़े मूल्य के अनुपात की अनुमानित अभिव्यक्ति कीमत ।
अनुमानित से अधिक सटीक तक, इस अनुपात को व्यक्त किया जा सकता है: आदि, जहां: 5+3=8, 8+5=13, आदि। या: 2,2:3,3:5,5:8,8, आदि ., जहां 2.2+3.3-5.5, आदि।

ग्राफ़िक रूप से, स्वर्णिम अनुपात को विभिन्न निर्माणों द्वारा प्राप्त खंडों के अनुपात द्वारा व्यक्त किया जा सकता है। हमारी राय में, चित्र में दिखाया गया निर्माण अधिक सुविधाजनक है। 169: यदि आप आधे वर्ग के विकर्ण में इसकी छोटी भुजा जोड़ते हैं, तो आपको इसकी लंबी भुजा के स्वर्णिम अंक के अनुपात में एक मान प्राप्त होता है।

चावल। 169. सुनहरे अनुपात 1.62:1 में एक आयत का ज्यामितीय निर्माण। खंडों (ए और बी) के संबंध में स्वर्ण संख्या 1.62

चावल। 170. स्वर्णिम अनुपात फ़ंक्शन 1.12:1 का ग्राफ़िक निर्माण

दो सुनहरे अनुपात का अनुपात

सद्भाव और संतुलन की एक दृश्य भावना पैदा करता है। दो आसन्न मात्राओं का एक और सामंजस्यपूर्ण अनुपात है, जिसे संख्या 1.12 द्वारा व्यक्त किया गया है। यह स्वर्णिम संख्या का एक कार्य है: यदि आप स्वर्णिम अनुपात के दो मानों के बीच का अंतर लेते हैं, इसे भी स्वर्णिम अनुपात में विभाजित करते हैं और प्रत्येक अंश को मूल स्वर्णिम अनुपात के छोटे मान में जोड़ते हैं, तो आपको एक अनुपात मिलता है 1.12 (चित्र 170)। इस संबंध में, उदाहरण के लिए, कुछ फ़ॉन्ट्स में एच, आर, जेड आदि अक्षरों में मध्य तत्व (शेल्फ) खींचा जाता है, विस्तृत अक्षरों के लिए ऊंचाई और चौड़ाई का अनुपात लिया जाता है, यह संबंध प्रकृति में भी पाया जाता है।

स्वर्णिम संख्या सामंजस्यपूर्ण रूप से विकसित व्यक्ति के अनुपात में देखी जाती है (चित्र 171): सिर की लंबाई कमर से सिर तक की दूरी को सुनहरे अनुपात में विभाजित करती है; नीकैप कमर से पैरों के तलवों तक की दूरी को भी विभाजित करता है; फैले हुए हाथ की मध्यमा उंगली की नोक किसी व्यक्ति की पूरी ऊंचाई को सुनहरे अनुपात में विभाजित करती है; उंगलियों के पर्वों का अनुपात भी एक स्वर्णिम संख्या है। यही घटना प्रकृति की अन्य संरचनाओं में भी देखी जाती है: मोलस्क के सर्पिलों में, फूलों के कोरोला में, आदि।

चावल। 172. नक्काशीदार जेरेनियम (पेलार्गोनियम) पत्ती का सुनहरा अनुपात। निर्माण: 1) स्केल ग्राफ़ का उपयोग करके (चित्र 171 देखें) क्या हम निर्माण करते हैं? एबीसी,	चावल। 173. पाँच पंखुड़ी और तीन पंखुड़ी वाली अंगूर की पत्तियाँ। लंबाई से चौड़ाई का अनुपात 1.12 है। स्वर्णिम अनुपात व्यक्त किया गया है

चित्र में. 172 और 173 सुनहरे नंबर 1.62 और 1.12 के अनुपात में एक जेरेनियम (पेलार्गोनियम) पत्ती और एक अंगूर की पत्ती के पैटर्न का निर्माण दिखाते हैं। जेरेनियम पत्ती में, निर्माण का आधार दो त्रिकोण हैं: एबीसी और सीईएफ, जहां उनमें से प्रत्येक की ऊंचाई और आधार का अनुपात संख्या 0.62 और 1.62 द्वारा व्यक्त किया जाता है, और सबसे दूर के बिंदुओं के तीन जोड़े के बीच की दूरी पत्ते बराबर हैं: AB=CE=SF. निर्माण को ड्राइंग में दर्शाया गया है। ऐसी पत्ती का डिज़ाइन जेरेनियम की तरह होता है, जिसमें समान नक्काशीदार पत्तियां होती हैं।

सामान्यीकृत गूलर के पत्ते (चित्र 173) का अनुपात अंगूर के पत्ते के समान है, 1.12 के अनुपात में, लेकिन अंगूर के पत्ते का बड़ा अनुपात उसकी लंबाई है, और समतल पेड़ के पत्ते का बड़ा अनुपात उसकी चौड़ाई है। गूलर के पत्ते में 1.62 के अनुपात में तीन आनुपातिक आकार होते हैं। वास्तुकला में इस तरह के पत्राचार को ट्रायड कहा जाता है (चार अनुपातों के लिए - टेट्राड और आगे: पेक्टैड, हेक्सोड)।

चित्र में. 174 सुनहरे अनुपात के अनुपात में मेपल का पत्ता बनाने की एक विधि दिखाता है। 1.12 की चौड़ाई और लंबाई के अनुपात के साथ, इसमें 1.62 संख्या के साथ कई अनुपात हैं। निर्माण दो ट्रेपेज़ॉइड पर आधारित है, जिसमें आधार की ऊंचाई और लंबाई का अनुपात एक सुनहरे अंक द्वारा व्यक्त किया जाता है। ड्राइंग में निर्माण दिखाया गया है, और मेपल के पत्ते के आकार के विकल्प भी दिए गए हैं।

ललित कला के कार्यों में, एक कलाकार या मूर्तिकार, सचेत रूप से या अवचेतन रूप से, अपनी प्रशिक्षित आंख पर भरोसा करते हुए, अक्सर आकार के अनुपात को सुनहरे अनुपात में लागू करता है। इस प्रकार, मसीह के सिर की एक प्रति पर काम करते समय (माइकल एंजेलो के अनुसार), इस पुस्तक के लेखक ने देखा कि उनके आकार में बालों के तारों में आसन्न कर्ल सुनहरे अनुपात के अनुपात को दर्शाते हैं, और उनके आकार में - आर्किमिडीयन सर्पिल , उलझा हुआ। पाठक स्वयं देख सकते हैं कि शास्त्रीय कलाकारों की कई पेंटिंगों में केंद्रीय आकृति प्रारूप के किनारों से सुनहरे अनुपात के अनुपात में दूरी पर स्थित है (उदाहरण के लिए, वी में लंबवत और क्षैतिज रूप से सिर की स्थिति) बोरोविकोवस्की का एम. आई. लोपुखिना का चित्र; ओ. किप्रेंस्की और अन्य द्वारा ए. एस. पुश्किन के चित्र में सिर के ऊर्ध्वाधर केंद्र के साथ स्थिति। यही चीज़ कभी-कभी क्षितिज रेखा (एफ. वासिलिव: "वेट मीडो", आई. लेविटन: "मार्च", "इवनिंग बेल्स") के स्थान के साथ देखी जा सकती है।

बेशक, यह नियम हमेशा रचना की समस्या का समाधान नहीं होता है, और इसे कलाकार के काम में लय और अनुपात की अंतर्ज्ञान को प्रतिस्थापित नहीं करना चाहिए। उदाहरण के लिए, यह ज्ञात है कि कुछ कलाकारों ने अपनी रचनाओं के लिए "संगीत संख्याओं" के अनुपात का उपयोग किया: तिहाई, चौथा, पांचवां (2: 3, 3: 4, आदि)। कला इतिहासकार, बिना कारण नहीं, ध्यान दें कि किसी भी शास्त्रीय वास्तुशिल्प स्मारक या मूर्तिकला का डिज़ाइन, यदि वांछित हो, तो किसी भी संख्या अनुपात में समायोजित किया जा सकता है। इस मामले में हमारा कार्य, और विशेष रूप से एक नौसिखिया कलाकार या वुडकार्वर का कार्य, यादृच्छिक संबंधों के अनुसार नहीं, बल्कि अभ्यास द्वारा सिद्ध सामंजस्यपूर्ण अनुपात के अनुसार अपने काम की एक जानबूझकर रचना बनाना सीखना है। इन सामंजस्यपूर्ण अनुपातों को उत्पाद के डिज़ाइन और आकार द्वारा पहचाना और जोर दिया जाना चाहिए।

सामंजस्यपूर्ण अनुपात खोजने के उदाहरण के रूप में, चित्र में दिखाए गए कार्य के लिए फ्रेम के आकार को निर्धारित करने पर विचार करें। 175. इसमें रखी गई छवि का प्रारूप सुनहरे अनुपात के अनुपात में सेट किया गया है। बाहरी आयामइसके किनारों की समान चौड़ाई वाले फ़्रेम सुनहरा अनुपात नहीं देंगे। इसलिए, इसकी लंबाई और चौड़ाई (ЗЗ0X220) का अनुपात स्वर्ण संख्या से थोड़ा कम माना जाता है, यानी 1.5 के बराबर, और पार्श्व पक्षों की तुलना में अनुप्रस्थ लिंक की चौड़ाई तदनुसार बढ़ जाती है। इससे प्रकाश में (पेंटिंग के लिए) फ्रेम के आयामों तक पहुंचना संभव हो गया, जिससे सुनहरे अनुपात का अनुपात मिला। फ़्रेम के निचले लिंक की चौड़ाई और उसके ऊपरी लिंक की चौड़ाई का अनुपात एक अन्य स्वर्ण संख्या, यानी 1.12 पर समायोजित किया जाता है। साथ ही, निचले लिंक की चौड़ाई और साइड लिंक की चौड़ाई का अनुपात (94:63) 1.5 के करीब है (चित्र में - बाईं ओर का विकल्प)।

आइए अब एक प्रयोग करें: हम निचले लिंक की चौड़ाई के कारण फ्रेम के लंबे हिस्से को 366 मिमी तक बढ़ा देंगे (यह 130 मिमी होगा) (चित्र में - दाईं ओर का विकल्प), जो न केवल लाएगा अनुपात करीब लेकिन सोने के भी
1.12 के बजाय 1.62 नंबर। परिणाम एक नई रचना है जिसका उपयोग किसी अन्य उत्पाद में किया जा सकता है, लेकिन फ्रेम के लिए इसे छोटा करने की इच्छा है। इसके निचले हिस्से को एक रूलर से इतना ढकें कि आंख परिणामी अनुपात को "स्वीकार" कर ले, और हमें इसकी लंबाई 330 मिमी मिल जाएगी, यानी हम मूल संस्करण के करीब पहुंच जाएंगे।

तो, विश्लेषण कर रहा हूँ विभिन्न विकल्प(चर्चित दोनों के अलावा अन्य भी हो सकते हैं), मास्टर अपने दृष्टिकोण से एकमात्र संभावित समाधान पर निर्णय लेता है।

एक साधारण उपकरण का उपयोग करके वांछित संरचना की खोज में सुनहरे अनुपात के सिद्धांत को लागू करना सबसे अच्छा है, जिसका मूल डिज़ाइन आरेख चित्र में दिखाया गया है। 176. इस उपकरण के दो रूलर, काज बी के चारों ओर घूमते हुए, एक मनमाना कोण बना सकते हैं। यदि, किसी भी कोण समाधान के लिए, हम दूरी AC को सुनहरे खंड में एक बिंदु K से विभाजित करते हैं और दो और शासकों को माउंट करते हैं: KM\\BC और KE\\AB बिंदु K, E और M पर टिका के साथ, तो किसी भी समाधान AC के लिए इस दूरी को सुनहरे अनुपात के संबंध में बिंदु K से विभाजित किया जाएगा।

विक्टर लाव्रस

स्वर्णिम अनुपात - हार्मोनिक अनुपात

गणित में अनुपात(अव्य. अनुपात)दो संबंधों की समानता को बुलाओ: ए : बी = सी : डी.

सीधा खंड अबनिम्नलिखित प्रकार से दो भागों में विभाजित किया जा सकता है:

दो बराबर भागों में - अब : ए.सी = अब : सूरज;

किसी भी दृष्टि से दो असमान भागों में (ऐसे भाग अनुपात नहीं बनाते);

इस प्रकार, जब अब : ए.सी = ए.सी : सूरज.

उत्तरार्द्ध चरम और औसत अनुपात में एक खंड का स्वर्णिम विभाजन या विभाजन है।

स्वर्णिम अनुपात एक खंड का असमान भागों में ऐसा आनुपातिक विभाजन है, जिसमें संपूर्ण खंड बड़े भाग से संबंधित होता है जैसे कि बड़ा भाग स्वयं छोटे से संबंधित होता है; या दूसरे शब्दों में, छोटा खंड बड़े के लिए है और बड़ा संपूर्ण के लिए है

ए : बी = बी : सीया साथ : बी = बी : ए.

चावल। 1.स्वर्णिम अनुपात की ज्यामितीय छवि

चावल। 2.सुनहरे अनुपात का उपयोग करके एक सीधी रेखा खंड को विभाजित करना। ईसा पूर्व = 1/2 अब; सीडी = ईसा पूर्व

बिंदु से मेंआधे के बराबर एक लंब बहाल किया जाता है अब. अंक प्राप्त हुआ साथएक रेखा द्वारा एक बिंदु से जुड़ा हुआ ए. परिणामी रेखा पर एक खंड अंकित किया गया है सूरजएक बिंदु के साथ समाप्त होना डी. खंड विज्ञापनप्रत्यक्ष में स्थानांतरित कर दिया गया अब. परिणामी बिंदु ईएक खंड को विभाजित करता है अबस्वर्णिम अनुपात अनुपात में.

सुनहरे अनुपात के गुणों को समीकरण द्वारा वर्णित किया गया है:

एक्स 2 - एक्स - 1 = 0.

इस समीकरण का हल:

दूसरा स्वर्णिम अनुपात

बल्गेरियाई पत्रिका "फादरलैंड" (नंबर 10, 1983) ने स्वेतन त्सेकोव-करंदश का एक लेख "ऑन द सेकेंड गोल्डन सेक्शन" प्रकाशित किया, जो मुख्य खंड से आता है और 44:56 का एक और अनुपात देता है।

चावल। 3.दूसरे स्वर्णिम अनुपात का निर्माण

विभाजन निम्नानुसार किया जाता है (चित्र 3 देखें)। खंड अबस्वर्णिम अनुपात के अनुसार विभाजित। बिंदु से साथलम्बवत बहाल है सीडी. RADIUS अबएक बात है डी, जो एक रेखा द्वारा एक बिंदु से जुड़ा होता है ए. समकोण एसीडीआधे में विभाजित है. बिंदु से साथएक रेखा तब तक खींची जाती है जब तक वह रेखा के साथ प्रतिच्छेद न कर दे विज्ञापन. डॉट ईएक खंड को विभाजित करता है विज्ञापन 56:44 के संबंध में।

चावल। 4.एक आयत को दूसरे सुनहरे अनुपात की रेखा से विभाजित करना

चित्र में. चित्र 4 दूसरे स्वर्णिम अनुपात की रेखा की स्थिति दर्शाता है। यह स्वर्ण अनुपात रेखा और आयत की मध्य रेखा के बीच में स्थित है।

स्वर्ण त्रिभुज

चावल। 5.एक नियमित पंचकोण और पंचग्राम का निर्माण

पेंटाग्राम बनाने के लिए, आपको एक नियमित पेंटागन बनाने की आवश्यकता है। इसके निर्माण की विधि जर्मन चित्रकार और ग्राफिक कलाकार अल्ब्रेक्ट ड्यूरर (1471...1528) द्वारा विकसित की गई थी। होने देना हे- वृत्त का केंद्र, ए- एक वृत्त पर एक बिंदु और ई- खंड के मध्य ओए. त्रिज्या के लंबवत ओए, बिंदु पर बहाल किया गया के बारे में, वृत्त को बिंदु पर प्रतिच्छेद करता है डी. कम्पास का उपयोग करके, व्यास पर एक खंड आलेखित करें सी.ई. = ईडी. एक वृत्त में अंकित एक नियमित पंचभुज की भुजा की लंबाई है डीसी. वृत्त पर खंड बिछाएँ डीसीऔर हमें एक नियमित पंचभुज बनाने के लिए पांच अंक मिलते हैं। हम पेंटागन के कोनों को विकर्णों के माध्यम से एक दूसरे से जोड़ते हैं और एक पेंटाग्राम प्राप्त करते हैं। पंचभुज के सभी विकर्ण एक दूसरे को सुनहरे अनुपात से जुड़े खंडों में विभाजित करते हैं।

चावल। 6.स्वर्ण त्रिभुज का निर्माण

हम एक प्रत्यक्ष कार्य करते हैं अब. बिंदु से एउस पर एक खंड तीन बार रखें के बारे मेंपरिणामी बिंदु के माध्यम से मनमाना मूल्य आररेखा पर एक लंब खींचिए अब, बिंदु के दाएं और बाएं लंबवत पर आरखंडों को अलग रखें के बारे में. अंक प्राप्त हुए डीऔर डी 1 एक बिंदु से सीधी रेखाओं से जुड़ें ए. खंड डीडीलाइन पर 1 लगाएं विज्ञापन 1, एक अंक प्राप्त करना साथ. उसने लाइन बांट दी विज्ञापनस्वर्णिम अनुपात के अनुपात में 1. पंक्तियां विज्ञापन 1 और डीडी 1 का उपयोग "सुनहरा" आयत बनाने के लिए किया जाता है।

स्वर्णिम अनुपात का इतिहास

यह आम तौर पर स्वीकार किया जाता है कि स्वर्णिम विभाजन की अवधारणा को प्राचीन यूनानी दार्शनिक और गणितज्ञ (छठी शताब्दी ईसा पूर्व) पाइथागोरस द्वारा वैज्ञानिक उपयोग में लाया गया था। ऐसी धारणा है कि पाइथागोरस ने स्वर्णिम विभाजन का अपना ज्ञान मिस्रियों और बेबीलोनियों से उधार लिया था। दरअसल, तूतनखामुन के मकबरे से चेप्स पिरामिड, मंदिर, आधार-राहतें, घरेलू सामान और आभूषणों के अनुपात से संकेत मिलता है कि मिस्र के कारीगरों ने उन्हें बनाते समय सुनहरे विभाजन के अनुपात का उपयोग किया था। फ्रांसीसी वास्तुकार ले कोर्बुसीयर ने पाया कि एबिडोस में फिरौन सेती प्रथम के मंदिर की राहत और फिरौन रामसेस को चित्रित करने वाली राहत में, आंकड़ों का अनुपात स्वर्ण प्रभाग के मूल्यों के अनुरूप है। वास्तुकार खेसीरा को उनके नाम पर बने मकबरे के एक लकड़ी के बोर्ड की राहत पर चित्रित किया गया है, उनके हाथों में मापने के उपकरण हैं जिनमें सुनहरे विभाजन के अनुपात दर्ज किए गए हैं।

चावल। 7.गतिशील आयतें

प्लेटो (427...347 ईसा पूर्व) को भी स्वर्णिम विभाजन का ज्ञान था। उनका संवाद "टाइमियस" पायथागॉरियन स्कूल के गणितीय और सौंदर्यवादी विचारों और विशेष रूप से स्वर्णिम प्रभाग के मुद्दों के लिए समर्पित है।

चावल। 8.प्राचीन स्वर्ण अनुपात कम्पास

प्राचीन साहित्य में जो हमारे सामने आया है, स्वर्णिम विभाजन का उल्लेख सबसे पहले यूक्लिड के तत्वों में किया गया था। "प्रिंसिपल्स" की दूसरी पुस्तक में स्वर्ण मंडल का ज्यामितीय निर्माण दिया गया है। यूक्लिड के बाद, स्वर्ण मंडल का अध्ययन हाइप्सिकल्स (द्वितीय शताब्दी ईसा पूर्व), पप्पस (तृतीय शताब्दी ईस्वी) और अन्य द्वारा किया गया था मध्ययुगीन यूरोप, सुनहरे विभाजन के साथ हम यूक्लिड के तत्वों के अरबी अनुवाद के माध्यम से मिले। नवरे (तृतीय शताब्दी) के अनुवादक जे. कैम्पानो ने अनुवाद पर टिप्पणियाँ कीं। स्वर्ण मंडल के रहस्यों को ईर्ष्यापूर्वक संरक्षित किया गया और सख्त गोपनीयता में रखा गया। वे केवल दीक्षार्थियों के लिए ही जाने जाते थे।

पुनर्जागरण के दौरान, ज्यामिति और कला दोनों में, विशेष रूप से वास्तुकला में इसके उपयोग के कारण वैज्ञानिकों और कलाकारों के बीच स्वर्ण प्रभाग में रुचि बढ़ गई, एक कलाकार और वैज्ञानिक लियोनार्डो दा विंची ने देखा कि इतालवी कलाकारों के पास बहुत अनुभवजन्य अनुभव था, लेकिन बहुत कम ज्ञान । उन्होंने कल्पना की और ज्यामिति पर एक किताब लिखना शुरू किया, लेकिन उसी समय भिक्षु लुका पैसिओली की एक किताब सामने आई और लियोनार्डो ने अपना विचार त्याग दिया। समकालीनों और विज्ञान के इतिहासकारों के अनुसार, लुका पैसिओली एक वास्तविक ज्योतिषी थे, जो फाइबोनैचि और गैलीलियो के बीच की अवधि में इटली के सबसे महान गणितज्ञ थे। लुका पैसिओली कलाकार पिएरो डेला फ्रांसेस्की के छात्र थे, जिन्होंने दो किताबें लिखीं, जिनमें से एक का नाम "ऑन पर्सपेक्टिव इन पेंटिंग" था। उन्हें वर्णनात्मक ज्यामिति का निर्माता माना जाता है।

लुका पैसिओली कला के लिए विज्ञान के महत्व को भली-भांति समझते थे। 1496 में, ड्यूक ऑफ़ मोरो के निमंत्रण पर, वह मिलान आये, जहाँ उन्होंने गणित पर व्याख्यान दिया। लियोनार्डो दा विंची ने उस समय मिलान में मोरो कोर्ट में भी काम किया था। 1509 में, लुका पैसिओली की पुस्तक "द डिवाइन प्रोपोर्शन" शानदार ढंग से निष्पादित चित्रों के साथ वेनिस में प्रकाशित हुई थी, यही कारण है कि यह माना जाता है कि वे लियोनार्डो दा विंची द्वारा बनाए गए थे। यह पुस्तक सुनहरे अनुपात का एक उत्साही भजन थी। सुनहरे अनुपात के कई फायदों के बीच, भिक्षु लुका पैसिओली इसके "दिव्य सार" को दिव्य त्रिमूर्ति की अभिव्यक्ति के रूप में नामित करने से नहीं चूके - भगवान पुत्र, भगवान पिता और भगवान पवित्र आत्मा (यह निहित था कि छोटा) खंड ईश्वर पुत्र का अवतार है, बड़ा खंड - ईश्वर पिता, और संपूर्ण खंड - पवित्र आत्मा का ईश्वर)।

लियोनार्डो दा विंची ने स्वर्ण मंडल के अध्ययन पर भी बहुत ध्यान दिया। उन्होंने नियमित पंचकोणों द्वारा गठित एक स्टीरियोमेट्रिक निकाय के खंड बनाए, और हर बार उन्होंने सुनहरे प्रभाग में पहलू अनुपात के साथ आयतें प्राप्त कीं। इसीलिए उन्होंने इस प्रभाग को यह नाम दिया सुनहरा अनुपात. इसलिए यह अभी भी सबसे लोकप्रिय बना हुआ है।

उसी समय, यूरोप के उत्तर में, जर्मनी में, अल्ब्रेक्ट ड्यूरर उन्हीं समस्याओं पर काम कर रहे थे। उन्होंने अनुपात पर ग्रंथ के पहले संस्करण का परिचय प्रस्तुत किया। ड्यूरर लिखते हैं. “यह आवश्यक है कि जो व्यक्ति कुछ करना जानता है, उसे इसे दूसरों को सिखाना चाहिए जिन्हें इसकी आवश्यकता है। मैंने यही करने का निश्चय किया है।”

ड्यूरर के एक पत्र को देखते हुए, इटली में रहते हुए उनकी मुलाकात लुका पैसिओली से हुई। अल्ब्रेक्ट ड्यूरर ने मानव शरीर के अनुपात के सिद्धांत को विस्तार से विकसित किया है। ड्यूरर ने अपने संबंधों की प्रणाली में सुनहरे वर्ग को एक महत्वपूर्ण स्थान दिया। किसी व्यक्ति की ऊंचाई को बेल्ट की रेखा के साथ-साथ निचले हाथों की मध्य उंगलियों की युक्तियों, मुंह के चेहरे के निचले हिस्से आदि के माध्यम से खींची गई रेखा द्वारा सुनहरे अनुपात में विभाजित किया जाता है। ड्यूरर का आनुपातिक दिशा सूचक यंत्र सर्वविदित है।

16वीं सदी के महान खगोलशास्त्री. जोहान्स केप्लर ने सुनहरे अनुपात को ज्यामिति के खजानों में से एक कहा। वह वनस्पति विज्ञान (पौधों की वृद्धि और उनकी संरचना) के लिए सुनहरे अनुपात के महत्व की ओर ध्यान आकर्षित करने वाले पहले व्यक्ति थे।

केप्लर ने सुनहरे अनुपात को स्व-निरंतरता कहा, "यह इस तरह से संरचित है," उन्होंने लिखा, "कि इस कभी न खत्म होने वाले अनुपात के दो सबसे निचले पद तीसरे पद में जुड़ते हैं, और कोई भी दो अंतिम पद, यदि एक साथ जोड़े जाते हैं। , अगला पद दें, और वही अनुपात अनंत तक बना रहता है।"

स्वर्णिम अनुपात के खंडों की श्रृंखला का निर्माण वृद्धि की दिशा (बढ़ती श्रृंखला) और कमी की दिशा (अवरोही श्रृंखला) दोनों में किया जा सकता है।

यदि मनमानी लंबाई की सीधी रेखा पर हों, तो खंड को अलग रख दें एम, खंड को इसके आगे रखें एम. इन दो खंडों के आधार पर, हम आरोही और अवरोही श्रृंखला के सुनहरे अनुपात के खंडों का एक पैमाना बनाते हैं

चावल। 9.स्वर्णिम अनुपात खंडों के पैमाने का निर्माण

बाद की शताब्दियों में, सुनहरे अनुपात का नियम एक अकादमिक सिद्धांत में बदल गया, और जब, समय के साथ, कला में अकादमिक दिनचर्या के खिलाफ संघर्ष शुरू हुआ, तो संघर्ष की गर्मी में "उन्होंने बच्चे को स्नान के पानी से बाहर फेंक दिया।" 19वीं सदी के मध्य में स्वर्णिम अनुपात की फिर से "खोज" की गई। 1855 में, सुनहरे अनुपात के जर्मन शोधकर्ता, प्रोफेसर ज़ीसिंग ने अपना काम "एस्थेटिक स्टडीज़" प्रकाशित किया। ज़ीसिंग के साथ जो हुआ वह बिल्कुल वैसा ही था जैसा एक शोधकर्ता के साथ अनिवार्य रूप से होना चाहिए जो अन्य घटनाओं के साथ संबंध के बिना किसी घटना को वैसा ही मानता है। उन्होंने प्रकृति और कला की सभी घटनाओं के लिए इसे सार्वभौमिक घोषित करते हुए, सुनहरे खंड के अनुपात को निरपेक्ष कर दिया। ज़ीसिंग के कई अनुयायी थे, लेकिन ऐसे विरोधी भी थे जिन्होंने अनुपात के उनके सिद्धांत को "गणितीय सौंदर्यशास्त्र" घोषित किया था।

चावल। 10.मानव शरीर के अंगों में स्वर्णिम अनुपात

ज़ीसिंग ने जबरदस्त काम किया। उसने लगभग दो हजार की माप की मानव शरीरऔर इस निष्कर्ष पर पहुंचे कि स्वर्णिम अनुपात औसत सांख्यिकीय नियम को व्यक्त करता है। नाभि बिंदु द्वारा शरीर का विभाजन स्वर्णिम अनुपात का सबसे महत्वपूर्ण संकेतक है। अनुपात पुरुष शरीर 13:8 = 1.625 के औसत अनुपात के भीतर उतार-चढ़ाव होता है और महिला शरीर के अनुपात की तुलना में कुछ हद तक सुनहरे अनुपात के करीब होता है, जिसके संबंध में अनुपात का औसत मूल्य 8:5 = 1.6 के अनुपात में व्यक्त किया जाता है। नवजात शिशु में यह अनुपात 1:1 होता है, 13 वर्ष की आयु तक यह 1.6 होता है, और 21 वर्ष की आयु तक यह एक पुरुष के बराबर होता है। सुनहरे अनुपात का अनुपात शरीर के अन्य हिस्सों के संबंध में भी दिखाई देता है - कंधे की लंबाई, अग्रबाहु और हाथ, हाथ और उंगलियां, आदि।

चावल। 11।मानव आकृति में स्वर्णिम अनुपात

ज़ीसिंग ने ग्रीक मूर्तियों पर अपने सिद्धांत की वैधता का परीक्षण किया। उन्होंने अपोलो बेल्वेडियर के अनुपात को सबसे अधिक विस्तार से विकसित किया। ग्रीक फूलदानों और स्थापत्य संरचनाओं की जांच की गई विभिन्न युग, पौधे, जानवर, पक्षियों के अंडे, संगीतमय स्वर, काव्य मीटर। ज़ीसिंग ने सुनहरे अनुपात की एक परिभाषा दी और दिखाया कि इसे सीधी रेखा खंडों और संख्याओं में कैसे व्यक्त किया जाता है। जब खंडों की लंबाई को व्यक्त करने वाली संख्याएं प्राप्त की गईं, तो ज़ीसिंग ने देखा कि उन्होंने एक फाइबोनैचि श्रृंखला का गठन किया, जिसे एक दिशा या दूसरे में अनिश्चित काल तक जारी रखा जा सकता है। उनकी अगली पुस्तक का शीर्षक था "द गोल्डन डिवीजन एज़ द बेसिक मॉर्फोलॉजिकल लॉ इन नेचर एंड आर्ट।" 1876 में, ज़ीसिंग के इस काम को रेखांकित करने वाली एक छोटी सी किताब, लगभग एक ब्रोशर, रूस में प्रकाशित हुई थी। लेखक ने प्रारंभिक यू.एफ.वी. के तहत शरण ली। इस संस्करण में चित्रकला के एक भी कार्य का उल्लेख नहीं है।

में देर से XIX- 20 वीं सदी के प्रारंभ में कला और वास्तुकला के कार्यों में सुनहरे अनुपात के उपयोग के बारे में कई विशुद्ध रूप से औपचारिक सिद्धांत सामने आए। डिज़ाइन और तकनीकी सौंदर्यशास्त्र के विकास के साथ, सुनहरे अनुपात का नियम कारों, फर्नीचर आदि के डिज़ाइन तक फैल गया।

फाइबोनैचि श्रृंखला

पीसा के इतालवी गणितज्ञ भिक्षु लियोनार्डो का नाम, जिसे फिबोनाची (बोनाची का पुत्र) के नाम से जाना जाता है, अप्रत्यक्ष रूप से सुनहरे अनुपात के इतिहास से जुड़ा हुआ है। उन्होंने पूर्व में बहुत यात्रा की, यूरोप को भारतीय (अरबी) अंकों से परिचित कराया। 1202 में, उनका गणितीय कार्य "द बुक ऑफ़ द अबेकस" (गिनती बोर्ड) प्रकाशित हुआ, जिसमें उस समय ज्ञात सभी समस्याओं को एकत्र किया गया था। समस्याओं में से एक में लिखा था, "एक वर्ष में एक जोड़े से कितने जोड़े खरगोश पैदा होंगे।" इस विषय पर विचार करते हुए, फाइबोनैचि ने संख्याओं की निम्नलिखित श्रृंखला बनाई:

संख्याओं की एक श्रृंखला 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, आदि। फाइबोनैचि श्रृंखला के रूप में जाना जाता है। संख्याओं के अनुक्रम की ख़ासियत यह है कि इसके प्रत्येक सदस्य, तीसरे से शुरू होकर, योग के बराबरपिछले दो 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34, आदि, और श्रृंखला में आसन्न संख्याओं का अनुपात स्वर्णिम विभाजन के अनुपात के करीब पहुंचता है। तो, 21: 34 = 0.617, और 34: 55 = 0.618। इस रिश्ते को प्रतीक द्वारा दर्शाया जाता है एफ. केवल यह अनुपात - 0.618: 0.382 - सुनहरे अनुपात में एक सीधी रेखा खंड का निरंतर विभाजन देता है, इसे अनंत तक बढ़ाता या घटाता है, जब छोटा खंड बड़े खंड से संबंधित होता है क्योंकि बड़ा खंड संपूर्ण से संबंधित होता है।

फाइबोनैचि व्यापार की व्यावहारिक आवश्यकताओं से भी निपटता है: किसी उत्पाद को तौलने के लिए उपयोग की जाने वाली वज़न की सबसे छोटी संख्या क्या है? फाइबोनैचि साबित करता है कि वजन की इष्टतम प्रणाली है: 1, 2, 4, 8, 16...

सामान्यीकृत स्वर्णिम अनुपात

फाइबोनैचि श्रृंखला केवल एक गणितीय घटना ही रह सकती थी, यदि यह तथ्य न होता कि पौधे और पशु जगत में स्वर्ण प्रभाग के सभी शोधकर्ता, कला का उल्लेख नहीं करते, हमेशा इस श्रृंखला में स्वर्ण के नियम की अंकगणितीय अभिव्यक्ति के रूप में आते थे विभाजन।

वैज्ञानिकों ने फाइबोनैचि संख्याओं और सुनहरे अनुपात के सिद्धांत को सक्रिय रूप से विकसित करना जारी रखा। यू. मटियासेविच फाइबोनैचि संख्याओं का उपयोग करके हिल्बर्ट की 10वीं समस्या को हल करता है। फाइबोनैचि संख्याओं और सुनहरे अनुपात का उपयोग करके कई साइबरनेटिक समस्याओं (खोज सिद्धांत, गेम, प्रोग्रामिंग) को हल करने के लिए सुरुचिपूर्ण तरीके उभर रहे हैं। संयुक्त राज्य अमेरिका में, गणितीय फाइबोनैचि एसोसिएशन भी बनाया जा रहा है, जो 1963 से एक विशेष पत्रिका प्रकाशित कर रहा है।

इस क्षेत्र में उपलब्धियों में से एक सामान्यीकृत फाइबोनैचि संख्या और सामान्यीकृत सुनहरे अनुपात की खोज है।

फाइबोनैचि श्रृंखला (1, 1, 2, 3, 5, 8) और उनके द्वारा खोजे गए वजन की "बाइनरी" श्रृंखला 1, 2, 4, 8, 16... पहली नज़र में पूरी तरह से अलग हैं। लेकिन उनके निर्माण के लिए एल्गोरिदम एक दूसरे के समान हैं: पहले मामले में, प्रत्येक संख्या पिछली संख्या का योग है जिसमें स्वयं 2 = 1 + 1 है; 4 = 2 + 2..., दूसरे में यह पिछली दो संख्याओं का योग है 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2.... क्या सामान्य गणितीय ज्ञात करना संभव है सूत्र जिससे हम प्राप्त करते हैं और "बाइनरी श्रृंखला और फाइबोनैचि श्रृंखला? या हो सकता है ये फार्मूला हमें नया दे दे संख्या सेट, कुछ नए अद्वितीय गुण रखने वाले?

दरअसल, आइए हम संख्यात्मक पैरामीटर सेट करें एस, जो कोई भी मान ले सकता है: 0, 1, 2, 3, 4, 5... एक संख्या श्रृंखला पर विचार करें, एस+ जिसके पहले पदों में से 1 इकाई है, और बाद के प्रत्येक पद पिछले एक के दो पदों के योग के बराबर है और पिछले एक से अलग किया गया है एसकदम. अगर एनहम इस श्रृंखला के वें पद को φ S से निरूपित करते हैं ( एन), तो हमें सामान्य सूत्र φ S ( एन) = φ एस ( एन- 1) + φ एस ( एन - एस - 1).

जाहिर सी बात है कि जब एस= 0 इस सूत्र से हमें एक "बाइनरी" श्रृंखला मिलती है एस= 1 - फाइबोनैचि श्रृंखला, के साथ एस= 2, 3, 4. संख्याओं की नई श्रृंखला कहलाती है एस-फाइबोनैचि संख्या.

कुल मिलाकर सुनहरा एस-अनुपात स्वर्णिम समीकरण का धनात्मक मूल है एस-सेक्शन x S+1 - x S - 1 = 0.

यह दिखाना आसान है कि कब एस= 0, खंड आधे में विभाजित है, और कब एस= 1 - परिचित शास्त्रीय स्वर्णिम अनुपात।

पड़ोसियों के बीच संबंध एस- फाइबोनैचि संख्याएं सोने की सीमा में पूर्ण गणितीय सटीकता के साथ मेल खाती हैं एस-अनुपात! ऐसे में गणितज्ञ कहते हैं कि सोना एस-अनुभाग संख्यात्मक अपरिवर्तनीय हैं एस-फाइबोनैचि संख्या.

सोने के अस्तित्व की पुष्टि करने वाले तथ्य एस-प्रकृति में अनुभाग, बेलारूसी वैज्ञानिक ई.एम. का हवाला देते हैं। सोरोको की पुस्तक "स्ट्रक्चरल हार्मनी ऑफ सिस्टम्स" (मिन्स्क, "साइंस एंड टेक्नोलॉजी", 1984)। उदाहरण के लिए, यह पता चला है कि अच्छी तरह से अध्ययन किए गए बाइनरी मिश्र धातुओं में विशेष, स्पष्ट कार्यात्मक गुण (थर्मल स्थिर, कठोर, पहनने के लिए प्रतिरोधी, ऑक्सीकरण प्रतिरोधी, आदि) केवल तभी होते हैं विशिष्ट गुरुत्वमूल घटक सोने में से एक द्वारा एक दूसरे से जुड़े हुए हैं एस-अनुपात. इससे लेखक को यह परिकल्पना प्रस्तुत करने की अनुमति मिली कि सोना एस-सेक्शन स्व-संगठित प्रणालियों के संख्यात्मक अपरिवर्तनीय हैं। एक बार प्रयोगात्मक रूप से पुष्टि हो जाने पर, यह परिकल्पना सहक्रिया विज्ञान के विकास के लिए मौलिक महत्व की हो सकती है - विज्ञान का एक नया क्षेत्र जो स्व-संगठित प्रणालियों में प्रक्रियाओं का अध्ययन करता है।

सोने के कोड का उपयोग करना एस-अनुपात को किसी भी वास्तविक संख्या द्वारा सोने की शक्तियों के योग के रूप में व्यक्त किया जा सकता है एस-पूर्णांक गुणांक के साथ अनुपात।

संख्याओं को एन्कोड करने की इस पद्धति के बीच मूलभूत अंतर यह है कि नए कोड के आधार सुनहरे होते हैं एस-अनुपात, साथ एस> 0 अपरिमेय संख्याएँ बनती हैं। इस प्रकार, अपरिमेय आधारों वाली नई संख्या प्रणालियाँ तर्कसंगत और अपरिमेय संख्याओं के बीच संबंधों के ऐतिहासिक रूप से स्थापित पदानुक्रम को "सिर से पैर तक" रखती प्रतीत होती हैं। तथ्य यह है कि प्राकृतिक संख्याओं की सबसे पहले "खोज" की गई थी; तो उनके अनुपात परिमेय संख्याएँ हैं। और केवल बाद में - पाइथागोरस द्वारा असंगत खंडों की खोज के बाद - अपरिमेय संख्याओं का जन्म हुआ। उदाहरण के लिए, दशमलव, क्विनरी, बाइनरी और अन्य शास्त्रीय स्थितीय संख्या प्रणालियों में, प्राकृतिक संख्याओं को एक प्रकार के मौलिक सिद्धांत के रूप में चुना गया था - 10, 5, 2 - जिनमें से निश्चित नियमअन्य सभी प्राकृतिक संख्याओं, साथ ही परिमेय और अपरिमेय संख्याओं का निर्माण किया गया।

अंकन के मौजूदा तरीकों का एक प्रकार का विकल्प एक मौलिक सिद्धांत के रूप में एक नई, अपरिमेय प्रणाली है, जिसकी शुरुआत एक अपरिमेय संख्या है (जो, याद रखें, सुनहरे अनुपात समीकरण की जड़ है); अन्य वास्तविक संख्याएँ इसके माध्यम से पहले से ही व्यक्त की जाती हैं।

ऐसी संख्या प्रणाली में, कोई भी प्राकृतिक संख्याहमेशा परिमित के रूप में प्रस्तुत करने योग्य - और अनंत नहीं, जैसा कि पहले सोचा गया था! - सोने में से किसी की डिग्री का योग एस-अनुपात. यही एक कारण है कि आश्चर्यजनक गणितीय सरलता और लालित्य से भरपूर "तर्कहीन" अंकगणित ने इसे आत्मसात कर लिया है। सर्वोत्तम गुणशास्त्रीय बाइनरी और फाइबोनैचि अंकगणित।

प्रकृति में गठन के सिद्धांत

जो कुछ भी किसी न किसी रूप में आया, वह बना, बढ़ा, अंतरिक्ष में जगह बनाने और खुद को संरक्षित करने का प्रयास किया। यह इच्छा मुख्य रूप से दो विकल्पों में साकार होती है - ऊपर की ओर बढ़ना या पृथ्वी की सतह पर फैलना और सर्पिल में घूमना।

खोल एक सर्पिल में मुड़ा हुआ है। यदि आप इसे खोलते हैं, तो आपको सांप की लंबाई से थोड़ी छोटी लंबाई मिलती है। एक छोटे से दस सेंटीमीटर के खोल में 35 सेमी लंबा सर्पिल होता है। सर्पिल प्रकृति में बहुत आम हैं। सर्पिल के बारे में बात किए बिना स्वर्णिम अनुपात का विचार अधूरा होगा।

चावल। 12.आर्किमिडीज़ सर्पिल

सर्पिलाकार घुंघराले खोल के आकार ने आर्किमिडीज़ का ध्यान आकर्षित किया। उन्होंने इसका अध्ययन किया और सर्पिल के लिए एक समीकरण तैयार किया। इस समीकरण के अनुसार खींचे गए सर्पिल को उनके नाम से पुकारा जाता है। उसके कदम में वृद्धि हमेशा एक समान होती है। वर्तमान में, आर्किमिडीज़ सर्पिल का व्यापक रूप से प्रौद्योगिकी में उपयोग किया जाता है।

गोएथे ने प्रकृति की सर्पिलता की प्रवृत्ति पर भी जोर दिया। पेड़ की शाखाओं पर पत्तियों की पेचदार और सर्पिल व्यवस्था बहुत पहले ही देखी गई थी। सर्पिल को सूरजमुखी के बीज, पाइन शंकु, अनानास, कैक्टि, आदि की व्यवस्था में देखा गया था। वनस्पतिशास्त्रियों और गणितज्ञों के संयुक्त कार्य ने इन पर प्रकाश डाला अद्भुत घटनाप्रकृति। यह पता चला कि फाइबोनैचि श्रृंखला एक शाखा (फाइलोटैक्सिस), सूरजमुखी के बीज और पाइन शंकु पर पत्तियों की व्यवस्था में प्रकट होती है, और इसलिए, सुनहरे अनुपात का नियम स्वयं प्रकट होता है। मकड़ी अपना जाल सर्पिल पैटर्न में बुनती है। एक तूफान सर्पिल की तरह घूम रहा है। डरा हुआ झुण्ड हिरनसर्पिल दूर. डीएनए अणु एक दोहरे हेलिक्स में मुड़ा हुआ है। गोएथे ने सर्पिल को "जीवन का वक्र" कहा।

सड़क किनारे जड़ी-बूटियों के बीच एक अनोखा पौधा उगता है - चिकोरी। आइए इस पर करीब से नज़र डालें। मुख्य तने से एक अंकुर बन गया है। पहला पत्ता वहीं स्थित था।

चावल। 13.कासनी

शूट अंतरिक्ष में एक मजबूत इजेक्शन करता है, रुकता है, एक पत्ती छोड़ता है, लेकिन इस बार यह पहले की तुलना में छोटा है, फिर से स्पेस में इजेक्शन करता है, लेकिन कम बल के साथ, इससे भी छोटे आकार की एक पत्ती छोड़ता है और फिर से बाहर निकल जाता है . यदि पहला उत्सर्जन 100 इकाइयों के रूप में लिया जाता है, तो दूसरा 62 इकाइयों के बराबर है, तीसरा - 38, चौथा - 24, आदि। पंखुड़ियों की लंबाई भी सुनहरे अनुपात के अधीन है। बढ़ते और अंतरिक्ष पर विजय प्राप्त करते समय, पौधे ने कुछ निश्चित अनुपात बनाए रखा। इसके विकास के आवेग सुनहरे अनुपात के अनुपात में धीरे-धीरे कम होते गए।

चावल। 14.विविपेरस छिपकली

पहली नज़र में, छिपकली का अनुपात हमारी आंखों को भाता है - इसकी पूंछ की लंबाई शरीर के बाकी हिस्सों की लंबाई से 62 से 38 तक संबंधित होती है।

पौधे और पशु जगत दोनों में, प्रकृति की रचनात्मक प्रवृत्ति लगातार टूटती रहती है - विकास और गति की दिशा के संबंध में समरूपता। यहां सुनहरा अनुपात विकास की दिशा के लंबवत भागों के अनुपात में दिखाई देता है।

प्रकृति ने विभाजन को सममित भागों और सुनहरे अनुपातों में किया है। भाग संपूर्ण संरचना की पुनरावृत्ति को प्रकट करते हैं।

चावल। 15.पक्षी का अंडा

महान गोएथे, एक कवि, प्रकृतिवादी और कलाकार (उन्होंने पानी के रंग बनाए और चित्रित किए), कार्बनिक निकायों के रूप, गठन और परिवर्तन का एक एकीकृत सिद्धांत बनाने का सपना देखा। यह वह थे जिन्होंने मॉर्फोलॉजी शब्द को वैज्ञानिक उपयोग में लाया।

इस सदी की शुरुआत में पियरे क्यूरी ने समरूपता के बारे में कई गहन विचार तैयार किए। उन्होंने तर्क दिया कि पर्यावरण की समरूपता को ध्यान में रखे बिना कोई भी किसी पिंड की समरूपता पर विचार नहीं कर सकता है।

"सुनहरे" समरूपता के पैटर्न ऊर्जा संक्रमण में प्रकट होते हैं प्राथमिक कण, कुछ रासायनिक यौगिकों की संरचना में, ग्रहों और ब्रह्मांडीय प्रणालियों में, जीवित जीवों की जीन संरचनाओं में। ये पैटर्न, जैसा कि ऊपर बताया गया है, व्यक्तिगत मानव अंगों और पूरे शरीर की संरचना में मौजूद हैं, और मस्तिष्क और दृश्य धारणा के बायोरिदम और कामकाज में भी खुद को प्रकट करते हैं।

स्वर्णिम अनुपात और समरूपता

समरूपता के संबंध के बिना, स्वर्णिम अनुपात पर अलग से विचार नहीं किया जा सकता है। महान रूसी क्रिस्टलोग्राफर जी.वी. वुल्फ (1863...1925) ने सुनहरे अनुपात को समरूपता की अभिव्यक्तियों में से एक माना।

स्वर्णिम विभाजन विषमता की अभिव्यक्ति नहीं है, आधुनिक विचारों के अनुसार, स्वर्णिम विभाजन असममित समरूपता है। समरूपता के विज्ञान में ऐसी अवधारणाएँ शामिल हैं स्थिरऔर गतिशील समरूपता. स्थैतिक समरूपता शांति और संतुलन की विशेषता है, जबकि गतिशील समरूपता गति और विकास की विशेषता है। इस प्रकार, प्रकृति में, स्थिर समरूपता क्रिस्टल की संरचना द्वारा दर्शायी जाती है, और कला में यह शांति, संतुलन और गतिहीनता की विशेषता है। गतिशील समरूपता गतिविधि को व्यक्त करती है, गति, विकास, लय की विशेषता बताती है, यह जीवन का प्रमाण है। स्थैतिक समरूपता समान खंडों और समान मूल्यों की विशेषता है। गतिशील समरूपता को खंडों में वृद्धि या उनकी कमी की विशेषता है, और इसे बढ़ती या घटती श्रृंखला के सुनहरे खंड के मूल्यों में व्यक्त किया जाता है।

साहित्य में स्वर्णिम अनुपात. कविता और स्वर्णिम अनुपात

काव्य कृतियों की संरचना में बहुत कुछ इस कला रूप को संगीत के समान बनाता है। एक स्पष्ट लय, तनावग्रस्त और बिना तनाव वाले अक्षरों का प्राकृतिक विकल्प, कविताओं का एक क्रमबद्ध मीटर और उनकी भावनात्मक समृद्धि कविता बनाती है बहनसंगीतमय कार्य. प्रत्येक छंद का अपना संगीत रूप होता है - अपनी लय और धुन। कोई उम्मीद कर सकता है कि कविताओं की संरचना में संगीत कार्यों की कुछ विशेषताएं, संगीत सद्भाव के नियम और, परिणामस्वरूप, सुनहरा अनुपात दिखाई देगा।

आइए कविता के आकार, यानी उसमें पंक्तियों की संख्या से शुरुआत करें। ऐसा प्रतीत होता है कि कविता का यह पैरामीटर मनमाने ढंग से बदल सकता है। हालाँकि, यह पता चला कि ऐसा नहीं था। उदाहरण के लिए, एन. वासुतिन्स्की का ए.एस. की कविताओं का विश्लेषण। इस दृष्टिकोण से पुश्किन ने दिखाया कि कविताओं के आकार बहुत असमान रूप से वितरित हैं; यह पता चला कि पुश्किन स्पष्ट रूप से 5, 8, 13, 21 और 34 लाइनों (फाइबोनैचि संख्या) के आकार को पसंद करते हैं।

कई शोधकर्ताओं ने देखा है कि कविताएँ संगीत के टुकड़ों के समान हैं; उनके पास अंतिम बिंदु भी हैं जो कविता को सुनहरे अनुपात के अनुपात में विभाजित करते हैं। उदाहरण के लिए, ए.एस. की कविता पर विचार करें। पुश्किन का "शूमेकर":

एक बार एक मोची पेंटिंग की तलाश में था
और उसने जूतों की गलती बताई;
कलाकार ने तुरंत अपना ब्रश उठाया और खुद को ठीक किया,
तो, अपनी बाहों अकीम्बो के साथ, मोची ने जारी रखा:
"मुझे लगता है कि चेहरा थोड़ा टेढ़ा है...
क्या ये स्तन भी नग्न नहीं हैं?
यहाँ एपेल्स ने अधीरता से टोकते हुए कहा:
"जज, मेरे दोस्त, बूट से ऊंचा कोई नहीं!"

मेरा एक दोस्त हैमन में:
मुझे नहीं पता कि वह किस विषय में है
वह एक विशेषज्ञ था, भले ही वह शब्दों में सख्त था,
परन्तु शैतान जगत का न्याय करने से उस से बैर रखता है:
जूतों का मूल्यांकन करने का प्रयास करें!

आइए इस दृष्टांत का विश्लेषण करें। कविता में 13 पंक्तियाँ हैं। इसके दो अर्थपूर्ण भाग हैं: पहला 8 पंक्तियों में और दूसरा (दृष्टान्त का नैतिक) 5 पंक्तियों में (13, 8, 5 फाइबोनैचि संख्याएँ हैं)।

पुश्किन की आखिरी कविताओं में से एक, "मैं ज़ोरदार अधिकारों को महत्व देता हूँ, प्रिय नहीं..." में 21 पंक्तियाँ हैं और इसके दो अर्थ भाग हैं: 13 और 8 पंक्तियाँ।

मैं ज़ोरदार अधिकारों को अधिक महत्व नहीं देता,
जिससे एक से ज्यादा लोगों का सिर घूम जाता है.
मुझे यह शिकायत नहीं है कि देवताओं ने इनकार कर दिया
करों को चुनौती देना मेरा सौभाग्य है
या राजाओं को आपस में लड़ने से रोकें;
और अगर प्रेस स्वतंत्र है तो मेरे लिए चिंता करना पर्याप्त नहीं है
मूर्खों को मूर्ख बनाना, या संवेदनशील सेंसरशिप
पत्रिका की योजनाओं में जोकर शर्मिंदा होता है।
आप देखिए, यह सब शब्द, शब्द, शब्द हैं।
अन्य, बेहतर अधिकार मुझे प्रिय हैं:
मुझे एक अलग, बेहतर आज़ादी चाहिए:
राजा पर निर्भर रहो, प्रजा पर निर्भर रहो -
क्या हमें परवाह है? भगवान उनके साथ रहें.
कोई नहीं
केवल अपने आप को रिपोर्ट न दें
सेवा करना और प्रसन्न करना; सत्ता के लिए, पोशाक के लिए
अपना विवेक, अपने विचार, अपनी गर्दन मत झुकाओ;
अपनी इच्छानुसार इधर-उधर घूमना,
प्रकृति के दिव्य सौन्दर्य से आश्चर्यचकित होकर,
और कला और प्रेरणा की रचनाओं से पहले
कोमलता के उल्लास में खुशी से कांपते हुए,
क्या खुशी है! यह सही है...

विशेषता यह है कि इस श्लोक का पहला भाग (13 पंक्तियाँ) अपनी अर्थात्मक सामग्री के अनुसार 8 और 5 पंक्तियों में विभाजित है, अर्थात् संपूर्ण काव्य स्वर्णिम अनुपात के नियमों के अनुसार संरचित है।

एन. वास्युटिंस्की द्वारा बनाया गया उपन्यास "यूजीन वनगिन" का विश्लेषण निस्संदेह रुचि का है। इस उपन्यास में 8 अध्याय हैं, प्रत्येक में औसतन लगभग 50 छंद हैं। आठवां अध्याय सबसे उत्तम, सबसे परिष्कृत और भावनात्मक रूप से समृद्ध है। इसमें 51 श्लोक हैं। यूजीन के तातियाना को लिखे पत्र (60 पंक्तियों) के साथ, यह बिल्कुल फाइबोनैचि संख्या 55 से मेल खाता है!

एन. वासुतिन्स्की कहते हैं:

"अध्याय की परिणति यूजीन द्वारा तात्याना के प्रति प्रेम की घोषणा है - पंक्ति "पीला हो जाना और मिट जाना... यह आनंद है!" यह पंक्ति पूरे आठवें अध्याय को दो भागों में विभाजित करती है - पहले में 477 पंक्तियाँ हैं, और दूसरे में - 295 पंक्तियाँ। उनका अनुपात 1.617 है! यह पुश्किन की प्रतिभा द्वारा परिपूर्ण सद्भाव का एक महान चमत्कार है!

लेर्मोंटोव की प्रसिद्ध कविता "बोरोडिनो" दो भागों में विभाजित है: वर्णनकर्ता को संबोधित एक परिचय और केवल एक छंद ("मुझे बताओ, चाचा, यह अकारण नहीं है..."), और मुख्य भाग, एक स्वतंत्र संपूर्ण का प्रतिनिधित्व करता है जो दो समान भागों में विभाजित होता है। उनमें से पहला बढ़ते तनाव के साथ युद्ध की प्रत्याशा का वर्णन करता है, दूसरा कविता के अंत तक तनाव में धीरे-धीरे कमी के साथ युद्ध का वर्णन करता है। इन भागों के बीच की सीमा कार्य का चरम बिंदु है और सुनहरे खंड द्वारा विभाजन के बिंदु पर बिल्कुल गिरती है।

कविता के मुख्य भाग में 13 सात पंक्तियाँ अर्थात् 91 पंक्तियाँ हैं। इसे सुनहरे अनुपात (91:1.618 = 56.238) से विभाजित करने के बाद, हम आश्वस्त हैं कि विभाजन बिंदु 57वें श्लोक की शुरुआत में है, जहां एक छोटा वाक्यांश है: "अच्छा, वह एक दिन था!". यह वह वाक्यांश है जो "उत्साहित प्रत्याशा के चरम बिंदु" का प्रतिनिधित्व करता है, कविता के पहले भाग (लड़ाई की प्रत्याशा) को पूरा करता है और इसके दूसरे भाग (लड़ाई का विवरण) को खोलता है।

इस प्रकार, स्वर्णिम अनुपात कविता में एक बहुत ही सार्थक भूमिका निभाता है, जो कविता के चरमोत्कर्ष को उजागर करता है।

वास्तुकला, मूर्तिकला, चित्रकला, फोटोग्राफी में स्वर्णिम अनुपात

प्राचीन यूनानी वास्तुकला की सबसे खूबसूरत कृतियों में से एक पार्थेनन (5वीं शताब्दी ईसा पूर्व) है।

आंकड़े सुनहरे अनुपात से जुड़े कई पैटर्न दिखाते हैं। इमारत के अनुपात को संख्या Ф=0.618 की विभिन्न घातों के माध्यम से व्यक्त किया जा सकता है...

पार्थेनन के फर्श योजना पर आप "सुनहरे आयत" भी देख सकते हैं:

हम कैथेड्रल भवन में स्वर्णिम अनुपात देख सकते हैं पेरिस का नोट्रे डेम(नोट्रे डेम डे पेरिस), और चेप्स के पिरामिड में:

तूतनखामुन के मकबरे से चेप्स पिरामिड, मंदिरों, आधार-राहतों, घरेलू वस्तुओं और गहनों के अनुपात से संकेत मिलता है कि मिस्र के कारीगरों ने उन्हें बनाते समय सुनहरे विभाजन के अनुपात का उपयोग किया था। फ्रांसीसी वास्तुकार ले कोर्बुसीयर ने पाया कि एबिडोस में फिरौन सेती प्रथम के मंदिर की राहत और फिरौन रामसेस को चित्रित करने वाली राहत में, आंकड़ों का अनुपात स्वर्ण प्रभाग के मूल्यों के अनुरूप है। वास्तुकार खेसीरा को उनके नाम पर बने मकबरे के एक लकड़ी के बोर्ड की राहत पर चित्रित किया गया है, उनके हाथों में मापने के उपकरण हैं जिनमें सुनहरे विभाजन के अनुपात दर्ज किए गए हैं।

जहाँ तक पिरामिडों की बात है, न केवल मिस्र के पिरामिड सुनहरे अनुपात के सही अनुपात के अनुसार बनाए गए थे; यही घटना मैक्सिकन पिरामिडों में भी पाई गई थी। पिरामिड का क्रॉस सेक्शन एक सीढ़ी के समान आकार दिखाता है। पहले स्तर में 16 सीढ़ियाँ हैं, दूसरे में 42 सीढ़ियाँ हैं और तीसरे में 68 सीढ़ियाँ हैं।
ये संख्याएँ फाइबोनैचि अनुपात पर इस प्रकार आधारित हैं:

16 x 1.618 = 26

26 x 1.618 = 42

सेंट बेसिल कैथेड्रल की वास्तुकला में कई सुनहरे अनुपात हैं:

कई प्राचीन मूर्तिकारों द्वारा सुनहरे अनुपात का उपयोग किया जाता था। अपोलो बेल्वेडियर की मूर्ति का सुनहरा अनुपात ज्ञात है: चित्रित व्यक्ति की ऊंचाई को सुनहरे खंड में नाभि रेखा द्वारा विभाजित किया गया है।

पुनर्जागरण में, कलाकारों ने पाया कि किसी भी चित्र में कुछ बिंदु होते हैं जो अनजाने में हमारा ध्यान आकर्षित करते हैं, तथाकथित दृश्य केंद्र। इस मामले में, इससे कोई फर्क नहीं पड़ता कि चित्र का प्रारूप क्या है - क्षैतिज या ऊर्ध्वाधर। ऐसे केवल चार बिंदु हैं; वे छवि आकार को क्षैतिज और लंबवत रूप से सुनहरे अनुपात में विभाजित करते हैं, अर्थात। वे समतल के संगत किनारों से लगभग 3/8 और 5/8 की दूरी पर स्थित हैं।

इस खोज को उस समय के कलाकारों द्वारा पेंटिंग का "सुनहरा अनुपात" कहा गया था। इसलिए, तस्वीर के मुख्य तत्व पर ध्यान आकर्षित करने के लिए, इस तत्व को दृश्य केंद्रों में से एक के साथ जोड़ना आवश्यक है।

चित्र में I.I. शिश्किन का "शिप ग्रोव" सुनहरे अनुपात के रूपांकनों को दर्शाता है। सूरज की रोशनी से जगमगाता एक देवदार का पेड़ (अग्रभूमि में खड़ा) पेंटिंग की लंबाई को लगभग सुनहरे अनुपात में विभाजित करता है। देवदार के पेड़ के दाहिनी ओर एक धूप से जगमगाती पहाड़ी है। यह चित्र के दाहिने हिस्से को सुनहरे अनुपात में क्षैतिज रूप से विभाजित करता है। मुख्य देवदार के बाईं ओर कई देवदार के पेड़ हैं - यदि वांछित है, तो आप चित्र को सुनहरे अनुपात के अनुपात में विभाजित करना सफलतापूर्वक जारी रख सकते हैं।

चित्र में उज्ज्वल ऊर्ध्वाधर और क्षैतिज की उपस्थिति, इसे सुनहरे अनुपात के संबंध में विभाजित करते हुए, इसे कलाकार के इरादे के अनुसार संतुलन और शांति का चरित्र देती है। जब कोई कलाकार तेजी से विकसित होने वाली क्रिया के साथ एक चित्र बनाता है, तो ऐसी ज्यामितीय रचना योजना (ऊर्ध्वाधर और क्षैतिज की प्रबलता के साथ) अस्वीकार्य हो जाती है।

गतिशीलता और उत्तेजना की भावना शायद किसी अन्य साधारण में सबसे अधिक दृढ़ता से प्रकट होती है ज्यामितीय आकृति- सर्पिल। राफेल द्वारा 1509 - 1510 में निष्पादित बहु-आकृति रचना, जब प्रसिद्ध चित्रकार ने वेटिकन में अपने भित्तिचित्र बनाए, कथानक की गतिशीलता और नाटकीयता से प्रतिष्ठित है। राफेल ने अपनी योजना को कभी पूरा नहीं किया, हालांकि, उनके स्केच को अज्ञात इतालवी ग्राफिक कलाकार मार्केंटिनियो रायमोंडी ने उकेरा था, जिन्होंने इस स्केच के आधार पर "मासूमों का नरसंहार" उत्कीर्णन बनाया था।

यदि, राफेल के प्रारंभिक रेखाचित्र में, हम मानसिक रूप से रचना के शब्दार्थ केंद्र से चलने वाली रेखाएँ खींचते हैं - वह बिंदु जहाँ योद्धा की उंगलियाँ बच्चे के टखने के चारों ओर बंद होती हैं - बच्चे की आकृतियों के साथ, महिला उसे अपने पास रखती है, योद्धा अपनी तलवार के साथ उठाया, और फिर स्केच के दाहिने हिस्सों पर उसी समूह के आंकड़ों के साथ (आकृति में ये रेखाएं लाल रंग में खींची गई हैं), और फिर इन टुकड़ों को एक घुमावदार बिंदीदार रेखा से जोड़ दें, फिर बहुत बड़ी सटीकता के साथ एक सुनहरा सर्पिल बनता है प्राप्त किया। इसे वक्र की शुरुआत से गुजरने वाली सीधी रेखाओं पर सर्पिल द्वारा काटे गए खंडों की लंबाई के अनुपात को मापकर जांचा जा सकता है।

यह अज्ञात है कि क्या राफेल ने "मासूमों का नरसंहार" रचना बनाते समय वास्तव में सुनहरा सर्पिल खींचा था या केवल इसे "महसूस" किया था। हालाँकि, हम विश्वास के साथ कह सकते हैं कि उत्कीर्णक रायमोंडी ने इस सर्पिल को देखा। इसका प्रमाण उनके द्वारा जोड़े गए रचना के नए तत्वों से मिलता है, जिसमें उन स्थानों पर सर्पिल के उलट पर जोर दिया गया है जहां यह केवल एक बिंदीदार रेखा द्वारा इंगित किया गया है। इन तत्वों को रायमोंडी के अंतिम उत्कीर्णन में देखा जा सकता है: महिला के सिर से फैला हुआ पुल का मेहराब रचना के बाईं ओर है और बच्चे का लेटा हुआ शरीर इसके केंद्र में है।

पेंटिंग में "सुनहरे अनुपात" के उदाहरणों पर आगे बढ़ते हुए, कोई भी लियोनार्डो दा विंची के काम पर ध्यान केंद्रित करने से बच नहीं सकता है। आइए पेंटिंग "ला जियोकोंडा" को करीब से देखें। चित्र की रचना "सुनहरे त्रिकोण" पर आधारित है।

आधुनिक मॉडलिंग व्यवसायआदर्श अनुपात का भी उपयोग करता है, क्योंकि "हर नई चीज़ अच्छी तरह से भुला दी गई पुरानी चीज़ है":

जानकारी का स्रोत:

कोवालेव एफ.वी. चित्रकला में स्वर्णिम अनुपात. के.: विश्चा स्कूल, 1989।

केप्लर I. हेक्सागोनल बर्फ के टुकड़े के बारे में। - एम., 1982.

ड्यूरर ए. डायरीज़, पत्र, ग्रंथ - एल., एम., 1957।

त्सेकोव-पेंसिल टी. दूसरे सुनहरे अनुपात के बारे में. - सोफिया, 1983।

स्टाखोव ए. सुनहरे अनुपात के कोड।

सुनहरे अनुपात के सिद्धांत के अनुसार निर्मित एक आयत से भुजा a वाले एक वर्ग को काटने पर, हमें समान गुणधर्म वाला एक नया, छोटा आयत प्राप्त होता है।

सुनहरा अनुभाग (सुनहरा अनुपात, चरम और औसत अनुपात में विभाजन, हार्मोनिक विभाजन, फ़िडियास संख्या) - एक निरंतर मूल्य का ऐसे अनुपात में भागों में विभाजन जिसमें बड़ा हिस्सा छोटे से संबंधित होता है क्योंकि पूरा मूल्य बड़े से संबंधित होता है। उदाहरण के लिए, किसी खंड को विभाजित करना ए.सीदो भागों में इस प्रकार बाँटें कि उसका अधिकांश भाग अबछोटे को संदर्भित करता है सूरजपूरे खंड की तरह ए.सीका अर्थ है अब(अर्थात | अब| / |सूरज| = |ए.सी| / |अब|).

यह अनुपात आमतौर पर दर्शाया जाता है यूनानी अक्षरϕ (पदनाम τ भी पाया जाता है)। यह इसके बराबर है:

"गोल्डन हार्मोनीज़" का सूत्र, उपरोक्त अनुपात को संतुष्ट करने वाली संख्याओं के जोड़े देता है:

किसी संख्या के मामले में, पैरामीटर एम = 1.

प्राचीन साहित्य में जो हमारे पास आया है, एक खंड को चरम और औसत अनुपात में विभाजित किया गया है (ἄκρος καὶ μέσος λόγος ) पहली बार यूक्लिड के तत्वों (सी. 300 ईसा पूर्व) में पाया गया, जहां इसका उपयोग नियमित पेंटागन के निर्माण के लिए किया जाता है।

सीपूर्वाह्नशब्द "गोल्डन रेशियो" (जर्मन)गोल्डनर श्नाइट) 1835 में जर्मन गणितज्ञ मार्टिन ओम द्वारा पेश किया गया था।

गणितीय गुण

पाँच-नक्षत्र वाले तारे में स्वर्णिम अनुपात

— तर्कहीनबीजगणितीय संख्या, निम्नलिखित समीकरणों में से किसी का सकारात्मक समाधान

एक सतत अंश द्वारा दर्शाया गया

के लिए जिनके उपयुक्त अंश क्रमिक फाइबोनैचि संख्याओं के अनुपात हैं। इस प्रकार, .

एक नियमित पांच-बिंदु वाले तारे में, प्रत्येक खंड को सुनहरे अनुपात में प्रतिच्छेद करने वाले एक खंड द्वारा विभाजित किया जाता है (अर्थात, नीले खंड का हरे से अनुपात, साथ ही लाल से नीला, साथ ही हरे से बैंगनी का अनुपात) , बराबर हैं)।

स्वर्णिम अनुपात का निर्माण

यहाँ एक और दृश्य है:

ज्यामितीय निर्माण

एक खंड का स्वर्णिम अनुपात अबनिम्नानुसार निर्माण किया जा सकता है: बिंदु पर बीके लिए सीधा अब, उस पर एक खंड रखें ईसा पूर्व, आधे के बराबर अब, खंड पर ए.सी.एक खंड अलग रखें विज्ञापन, बराबर ए.सी. − सी.बी., और अंत में, खंड पर अबएक खंड अलग रखें ए.ई., बराबर विज्ञापन. तब

स्वर्णिम अनुपात और सामंजस्य

यह आम तौर पर स्वीकार किया जाता है कि "गोल्डन रेशियो" वाली वस्तुओं को लोग सबसे सामंजस्यपूर्ण मानते हैं। तूतनखामुन के मकबरे से चेप्स पिरामिड, मंदिरों, आधार-राहतों, घरेलू वस्तुओं और गहनों के अनुपात से कथित तौर पर संकेत मिलता है कि मिस्र के कारीगरों ने उन्हें बनाते समय सुनहरे खंड के अनुपात का उपयोग किया था। वास्तुकार ले कोर्बुसीयर ने "पाया" कि एबिडोस में फिरौन सेती प्रथम के मंदिर की राहत और फिरौन रामसेस को चित्रित करने वाली राहत में, आंकड़ों का अनुपात सुनहरे अनुपात के मूल्यों के अनुरूप है। वास्तुकार खेसिरा को उनके नाम पर बने मकबरे के लकड़ी के बोर्ड की राहत पर चित्रित किया गया है, उनके हाथों में मापने के उपकरण हैं जिनमें सुनहरे खंड के अनुपात दर्ज हैं। पार्थेनन के प्राचीन यूनानी मंदिर के अग्रभाग में सुनहरे अनुपात हैं। इसकी खुदाई के दौरान, कम्पास की खोज की गई थी जिसका उपयोग प्राचीन दुनिया के वास्तुकारों और मूर्तिकारों द्वारा किया जाता था। पोम्पियन कम्पास (नेपल्स में संग्रहालय) में स्वर्ण मंडल के अनुपात आदि भी शामिल हैं।

कला में "सुनहरा अनुपात"।

स्वर्णिम अनुपात और दृश्य केंद्र

लियोनार्डो दा विंची से शुरुआत करते हुए, कई कलाकारों ने जानबूझकर सुनहरे अनुपात के अनुपात का उपयोग किया।

यह ज्ञात है कि सर्गेई ईसेनस्टीन ने "गोल्डन रेशियो" के नियमों के अनुसार कृत्रिम रूप से फिल्म बैटलशिप पोटेमकिन का निर्माण किया था। उन्होंने टेप को पांच हिस्सों में तोड़ दिया. पहले तो तीन क्रियाजहाज पर प्रकट होता है. पिछले दो में - ओडेसा में, जहां विद्रोह सामने आ रहा है। शहर में यह परिवर्तन बिल्कुल स्वर्णिम अनुपात बिंदु पर होता है। और प्रत्येक भाग का अपना फ्रैक्चर होता है, जो स्वर्णिम अनुपात के नियम के अनुसार होता है। एक फ्रेम, दृश्य, एपिसोड में विषय के विकास में एक निश्चित छलांग होती है: कथानक, मनोदशा। आइज़ेंस्टीन का मानना था कि चूंकि ऐसा संक्रमण सुनहरे अनुपात बिंदु के करीब है, इसलिए इसे सबसे तार्किक और प्राकृतिक माना जाता है।

सिनेमैटोग्राफी में गोल्डन रेशियो नियम के उपयोग का एक और उदाहरण विशेष बिंदुओं - "दृश्य केंद्र" पर फ्रेम के मुख्य घटकों का स्थान है। अक्सर चार बिंदुओं का उपयोग किया जाता है, जो समतल के संगत किनारों से 3/8 और 5/8 की दूरी पर स्थित होते हैं।

यह ध्यान दिया जाना चाहिए कि उपरोक्त उदाहरणों में "सुनहरा अनुपात" का अनुमानित मूल्य दिखाई दिया: यह सत्यापित करना आसान है कि न तो 3/2 और न ही 5/3 सुनहरे अनुपात के मूल्य के बराबर है।

रूसी वास्तुकार ज़ोल्तोव्स्की ने भी सुनहरे अनुपात का उपयोग किया था।

स्वर्णिम अनुपात की आलोचना

ऐसी राय है कि कला, वास्तुकला और प्रकृति में सुनहरे अनुपात का महत्व अतिरंजित है और गलत गणनाओं पर आधारित है।

आयतों के इष्टतम पक्षानुपात पर चर्चा करते समय (कागज आकार A0 और गुणज, फोटोग्राफिक प्लेट आकार (6:9, 9:12) या फिल्म फ्रेम (अक्सर 2:3), फिल्म और टेलीविजन स्क्रीन आकार - उदाहरण के लिए, 3:4 या 9:16) विभिन्न विकल्पों का परीक्षण किया गया। ऐसा हुआ अधिकांश लोगों को सोना समझ में नहीं आताअनुभाग को इष्टतम मानता है और इसके अनुपात को "बहुत लम्बा" मानता है।

पढ़ने की संख्या: 8113