Funkcijas grafika pieskares vienādojums

P. Romanovs, T. Romanova,
Magņitogorska,
Čeļabinskas apgabals

Funkcijas grafika pieskares vienādojums

Raksts publicēts ar viesnīcu kompleksa ITAKA+ atbalstu. Uzturoties Severodvinskas kuģu būvētāju pilsētā, jūs nesaskarsities ar pagaidu mājokļa atrašanas problēmu. , vietnē viesnīcu komplekss“ITHAKA+” http://itakaplus.ru, Jūs varat ērti un ātri izīrēt dzīvokli pilsētā uz jebkuru laika periodu ar ikdienas maksājumu.

Ieslēgts mūsdienu skatuve izglītības attīstība, viens no tās galvenajiem uzdevumiem ir radoši domājošas personības veidošana. Radošuma spējas skolēnos var attīstīt tikai tad, ja viņi sistemātiski tiek iesaistīti pētnieciskās darbības pamatos. Pamatu audzēkņu radošo spēku, spēju un talantu izmantošanai veido pilnvērtīgas zināšanas un prasmes. Šajā sakarā ne mazāk svarīga ir pamatzināšanu un prasmju sistēmas veidošanas problēma katrai skolas matemātikas kursa tēmai. Tajā pašā laikā pilnvērtīgām prasmēm jābūt nevis atsevišķu uzdevumu didaktiskajam mērķim, bet gan rūpīgi pārdomātai to sistēmai. Plašākajā nozīmē sistēma tiek saprasta kā savstarpēji saistītu mijiedarbīgu elementu kopums, kam ir integritāte un stabila struktūra.

Apskatīsim paņēmienu, kā iemācīt studentiem uzrakstīt vienādojumu funkcijas grafika pieskarei. Būtībā visas pieskares vienādojuma atrašanas problēmas ir saistītas ar nepieciešamību no līniju kopas (saitas, saimes) izvēlēties tās, kas atbilst noteiktai prasībai - tās ir pieskares noteiktas funkcijas grafikam. Šajā gadījumā līniju kopu, no kurām tiek veikta atlase, var norādīt divos veidos:

a) punkts, kas atrodas uz xOy plaknes (centrālais līniju zīmulis);
b) leņķiskais koeficients (paralēlais taisnu staru kūlis).

Šajā sakarā, pētot tēmu “Funkcijas grafika pieskares”, lai izolētu sistēmas elementus, mēs identificējām divu veidu problēmas:

1) uzdevumi pieskarei, ko nosaka punkts, caur kuru tā iet;
2) problēmas uz pieskares, ko dod tās slīpums.

Apmācība tangentes problēmu risināšanā tika veikta, izmantojot A.G. piedāvāto algoritmu. Mordkovičs. Viņa principiāla atšķirība no jau zināmajiem ir tas, ka pieskares punkta abscisu apzīmē ar burtu a (nevis x0), un tāpēc pieskares vienādojums iegūst formu

y = f(a) + f "(a) (x - a)

(salīdziniet ar y = f(x 0) + f "(x 0) (x - x 0)). metodiskā tehnika, mūsuprāt, ļauj studentiem ātri un viegli saprast, kur vispārējā pieskares vienādojumā ir ierakstītas pašreizējā punkta koordinātas un kur atrodas pieskares punkti.

Funkcijas y = f(x) grafika pieskares vienādojuma sastādīšanas algoritms

1. Pieskares punkta abscisu apzīmē ar burtu a.
2. Atrodiet f(a).
3. Atrodiet f "(x) un f "(a).
4. Atrastos skaitļus a, f(a), f "(a) aizstājiet ar vispārējais vienādojums pieskares y = f(a) = f "(a)(x – a).

Šo algoritmu var sastādīt, pamatojoties uz studentu patstāvīgu darbību identificēšanu un to izpildes secību.

Prakse ir parādījusi, ka katras galvenās problēmas secīgs risinājums, izmantojot algoritmu, ļauj attīstīt prasmes rakstīt funkcijas grafika pieskares vienādojumu pa posmiem, un algoritma soļi kalpo kā atskaites punkti darbībām. . Šī pieeja atbilst P.Ya izstrādātajai teorijai par pakāpenisku garīgo darbību veidošanos. Galperins un N.F. Taļizina.

Pirmā veida uzdevumos tika noteikti divi galvenie uzdevumi:

• pieskare iet caur punktu, kas atrodas uz līknes (1. uzdevums);
• tangenss iet caur punktu, kas neatrodas uz līknes (2. uzdevums).

1. uzdevums. Uzrakstiet funkcijas grafika pieskares vienādojumu punktā M(3; – 2).

Risinājums. Punkts M(3; – 2) ir pieskares punkts, jo

1. a = 3 – pieskares punkta abscisa.
2. f(3) = – 2.
3. f "(x) = x 2–4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – pieskares vienādojums.

2. uzdevums. Uzrakstiet visu pieskares vienādojumus funkcijas y = – x 2 – 4x + 2 grafikam, kas iet caur punktu M(– 3; 6).

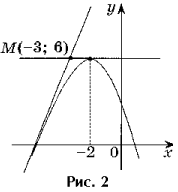Risinājums. Punkts M(– 3; 6) nav pieskares punkts, jo f(– 3) 6 (2. att.).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – pieskares vienādojums.

Pieskares iet caur punktu M(– 3; 6), tāpēc tās koordinātes apmierina pieskares vienādojumu.

6 = – a 2 – 4a + 2 – 2(a + 2) (– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.

Ja a = – 4, tad pieskares vienādojums ir y = 4x + 18.

Ja a = – 2, tad pieskares vienādojumam ir forma y = 6.

Otrajā veidā galvenie uzdevumi būs šādi:

• pieskare ir paralēla kādai taisnei (3. uzdevums);
• pieskare iet noteiktā leņķī pret doto taisni (4. uzdevums).

3. uzdevums. Uzrakstiet visu pieskares vienādojumus funkcijas y = x 3 grafikā – 3x 2 + 3, paralēli taisnei y = 9x + 1.

Risinājums.

1. a – pieskares punkta abscisa.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 - 6a.

Bet, no otras puses, f "(a) = 9 (paralēlisma nosacījums). Tas nozīmē, ka jāatrisina vienādojums 3a 2 – 6a = 9. Tā saknes ir a = – 1, a = 3 (3. att.). ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9 (x + 1);

y = 9x + 8 – pieskares vienādojums;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9 (x – 3);

y = 9x – 24 – pieskares vienādojums.

4. uzdevums. Uzrakstiet funkcijas y = 0,5x 2 – 3x + 1 grafika pieskares vienādojumu, kas iet 45° leņķī pret taisni y = 0 (4. att.).

Risinājums. No nosacījuma f "(a) = tan 45° mēs atrodam a: a – 3 = 1^a = 4.

1. a = 4 – pieskares punkta abscisa.
2. f(4) = 8–12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1 (x – 4).

y = x – 7 – pieskares vienādojums.

Ir viegli parādīt, ka jebkuras citas problēmas risināšana nozīmē vienas vai vairāku galveno problēmu atrisināšanu. Apsveriet šādas divas problēmas kā piemēru.

1. Uzrakstiet parabolas y = 2x 2 – 5x – 2 pieskares vienādojumus, ja pieskares krustojas taisnā leņķī un viena no tām pieskaras parabolai punktā ar abscisu 3 (5. att.).

Risinājums. Tā kā pieskares punkta abscisa ir dota, risinājuma pirmā daļa tiek reducēta uz galveno problēmu 1.

1. a = 3 – taisnā leņķa vienas malas pieskares punkta abscisa.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – pirmās pieskares vienādojums.

Ļaujiet a – pirmās pieskares slīpuma leņķis. Tā kā pieskares ir perpendikulāras, tad ir otrās pieskares slīpuma leņķis. No pirmās pieskares vienādojuma y = 7x – 20 mums ir tg a = 7. Atradīsim

Tas nozīmē, ka otrās pieskares slīpums ir vienāds ar .

Tālākais risinājums ir 3. galvenais uzdevums.

Tad lai B(c; f(c)) ir otrās rindas pieskares punkts

1. – otrā pieskares punkta abscisa.
2.
3.
4.
– otrās pieskares vienādojums.

Piezīme. Pieskares leņķisko koeficientu var vieglāk atrast, ja studenti zina perpendikulāru taisnes koeficientu attiecību k 1 k 2 = – 1.

2. Uzrakstiet visu kopīgo pieskares vienādojumus funkciju grafikos

Risinājums. Uzdevums ir atrast kopējo pieskares punktu abscisu, tas ir, atrisināt 1. galveno uzdevumu vispārīgā formā, izveidot vienādojumu sistēmu un pēc tam to atrisināt (6. att.).

1. Funkcijas y = x 2 + x + 1 grafikā esošā pieskares punkta abscisa ir a.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1) (x – a) = (2a + 1)x + 1 – a 2 .

1. Pieskares punkta abscisei c, kas atrodas uz funkcijas grafika
2.
3. f "(c) = c.
4.

Tā kā pieskares ir vispārīgas, tad

Tātad y = x + 1 un y = – 3x – 3 ir kopējās pieskares.

Aplūkojamo uzdevumu galvenais mērķis ir sagatavot studentus patstāvīgi atpazīt galvenās problēmas veidu, risinot sarežģītākas problēmas, kurām nepieciešamas noteiktas pētnieciskās prasmes (spēja analizēt, salīdzināt, vispārināt, izvirzīt hipotēzi u.c.). Šādi uzdevumi ietver jebkuru uzdevumu, kurā galvenais uzdevums ir iekļauts kā sastāvdaļa. Kā piemēru aplūkosim funkciju (apgriezti 1. uzdevumam) atrast funkciju no tās pieskares saimes.

3. Kādam b un c ir taisnes y = x un y = – 2x pieskares funkcijas y = x 2 + bx + c grafikam?

Risinājums.

Pieņemsim, ka t ir taisnes y = x pieskares punkta abscisa ar parabolu y = x 2 + bx + c; p ir taisnes y = – 2x pieskares punkta abscisa ar parabolu y = x 2 + bx + c. Tad pieskares vienādojums y = x iegūs formā y = (2t + b)x + c – t 2 , bet pieskares vienādojums y = – 2x būs y = (2p + b)x + c – p 2 .

Sastādām un atrisināsim vienādojumu sistēmu

Atbilde:

Problēmas, kas jārisina patstāvīgi

1. Uzrakstiet funkcijas y = 2x 2 – 4x + 3 grafikam uzzīmēto pieskares vienādojumus grafa krustpunktos ar taisni y = x + 3.

Atbilde: y = – 4x + 3, y = 6x – 9,5.

2. Kurām a vērtībām funkcijas y = x 2 – ax grafikam novilktā pieskare grafa punktā ar abscisu x 0 = 1 iet caur punktu M(2; 3)?

Atbilde: a = 0,5.

3. Kurām p vērtībām taisne y = px – 5 pieskaras līknei y = 3x 2 – 4x – 2?

Atbilde: p 1 = – 10, p 2 = 2.

4. Atrodiet visus funkcijas y = 3x – x 3 grafa kopīgos punktus un šim grafikam caur punktu P(0; 16) novilkto tangensu.

Atbilde: A(2; – 2), B(– 4; 52).

5. Atrodiet īsāko attālumu starp parabolu y = x 2 + 6x + 10 un taisni

Atbilde:

6. Līknē y = x 2 – x + 1 atrodiet punktu, kurā grafika pieskare ir paralēla taisnei y – 3x + 1 = 0.

Atbilde: M(2; 3).

7. Uzrakstiet funkcijas y = x 2 + 2x – grafika pieskares vienādojumu | 4x |, kas tam pieskaras divos punktos. Izveidojiet zīmējumu.

Atbilde: y = 2x – 4.

8. Pierādīt, ka taisne y = 2x – 1 nekrustojas ar līkni y = x 4 + 3x 2 + 2x. Atrodiet attālumu starp to tuvākajiem punktiem.

Atbilde:

9. Uz parabolas y = x 2 tiek ņemti divi punkti ar abscisēm x 1 = 1, x 2 = 3. Caur šiem punktiem tiek novilkts sekants. Kurā parabolas punktā tai pieskare būs paralēla sekantam? Uzrakstiet sekanta un pieskares vienādojumus.

Atbilde: y = 4x – 3 – sekanta vienādojums; y = 4x – 4 – pieskares vienādojums.

10. Atrodiet leņķi q starp pieskarēm funkcijas y = x 3 grafikam – 4x 2 + 3x + 1, kas novilktas punktos ar abscisēm 0 un 1.

Atbilde: q = 45°.

11. Kuros punktos funkcijas grafika pieskare veido 135° leņķi ar Ox asi?

Atbilde: A(0; – 1), B(4; 3).

12. Punktā A(1; 8) līdz līknei tiek novilkta tangensa. Atrodiet pieskares segmenta garumu starp koordinātu asīm.

Atbilde:

13. Uzrakstiet visu kopīgo pieskares vienādojumu funkciju y = x 2 – x + 1 un y = 2x 2 – x + 0,5 grafikiem.

Atbilde: y = – 3x un y = x.

14. Atrodiet attālumu starp funkcijas grafika pieskarēm paralēli x asij.

Atbilde:

15. Nosakiet, kādos leņķos parabola y = x 2 + 2x – 8 krustojas ar x asi.

Atbilde: q 1 = arctan 6, q 2 = arctan (– 6).

16.Funkciju grafiks atrast visus punktus, kuru katra pieskare šim grafikam krusto pozitīvās koordinātu pusasis, nogriežot no tiem vienādus segmentus.

Atbilde: A(– 3; 11).

17. Taisne y = 2x + 7 un parabola y = x 2 – 1 krustojas punktos M un N. Atrodiet to taisnes krustpunktu K, kas pieskaras parabolai punktos M un N.

Atbilde: K(1; – 9).

18. Kurām b vērtībām līnija y = 9x + b ir pieskares funkcijas y = x 3 – 3x + 15 grafikam?

Atbilde: – 1; 31.

19. Kurām k vērtībām taisnei y = kx – 10 ir tikai viens kopīgs punkts ar funkcijas y = 2x 2 + 3x – 2 grafiku? Atrastajām k vērtībām nosakiet punkta koordinātas.

Atbilde: k 1 = – 5, A(– 2; 0); k 2 = 11, B(2; 12).

20. Kurām b vērtībām funkcijas y = bx 3 – 2x 2 – 4 grafikam pieskare punktā ar abscisu x 0 = 2 iet caur punktu M(1; 8)?

Atbilde: b = – 3.

21. Parabola ar virsotni uz Vērša ass pieskaras taisnei, kas iet caur punktiem A(1; 2) un B(2; 4) punktā B. Atrodi parabolas vienādojumu.

Atbilde:

22. Pie kādas koeficienta k vērtības parabola y = x 2 + kx + 1 pieskaras Vērša asij?

Atbilde: k = d 2.

23. Atrodiet leņķus starp taisni y = x + 2 un līkni y = 2x 2 + 4x – 3.

29. Atrast attālumu starp funkcijas grafika pieskarēm un ģeneratoriem ar Ox ass pozitīvo virzienu 45° leņķī.

Atbilde:

30. Atrodiet visu y = x 2 + ax + b formas parabolu virsotņu lokusu, kas pieskaras taisnei y = 4x – 1.

Atbilde: taisna līnija y = 4x + 3.

Literatūra

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra un analīzes sākums: 3600 uzdevumi skolēniem un universitātēs iestājas. – M., Bustards, 1999.
2. Mordkovičs A. Seminārs četri jaunajiem skolotājiem. Tēma: Atvasinātās lietojumprogrammas. – M., “Matemātika”, Nr.21/94.
3. Zināšanu un prasmju veidošana, balstoties uz psihisko darbību pakāpeniskas asimilācijas teoriju.

/ Red. P.Ya. Galperiņa, N.F. Taļizina.– M., Maskavas Valsts universitāte, 1968. 1. piemērs.(Dota funkcija) = 3Dota funkcija 2 + 4Dota funkcija f 1. piemērs.(Dota funkcija x Dota funkcija 0 = 1.

Risinājums.– 5. Uzrakstīsim funkcijas grafika pieskares vienādojumu 1. piemērs.(Dota funkcija) grafika punktā ar abscisu Funkcijas atvasinājums ) pastāv jebkuram x

= (3Dota funkcija 2 + 4Dota funkcija R Dota funkcija + 4.

. Atradīsim viņu: 1. piemērs.(Dota funkcija 0) = 1. piemērs.(1) = 2; (Dota funkcija– 5)′ = 6

Tad = (Dota funkcija 0) (Dota funkcija – Dota funkcija 0) + 1. piemērs.(Dota funkcija 0),

Tad = 10(Dota funkcija – 1) + 2,

Tad = 10Dota funkcija – 8.

0) = = 10. Pieskares vienādojumam ir šāda forma: Tad = 10Dota funkcija – 8.

y– M., Maskavas Valsts universitāte, 1968. 1. piemērs.(Dota funkcija) = Dota funkcija 3 – 3Dota funkcija 2 + 2Dota funkcija Atbilde. 1. piemērs.(Dota funkcija 2. piemērs. + 5. Uzrakstīsim funkcijas grafika pieskares vienādojumu = 2Dota funkcija – 11.

Risinājums.– 5. Uzrakstīsim funkcijas grafika pieskares vienādojumu 1. piemērs.(Dota funkcija) grafika punktā ar abscisu Funkcijas atvasinājums ) pastāv jebkuram x

= (Dota funkcija 3 – 3Dota funkcija 2 + 2Dota funkcija), paralēli līnijai Dota funkcija 2 – 6Dota funkcija + 2.

y 1. piemērs.(Dota funkcija+ 5)′ = 3 Dota funkcija Kopš funkcijas grafika pieskares + 5. Uzrakstīsim funkcijas grafika pieskares vienādojumu = 2Dota funkcija) abscisu punktā Dota funkcija 0 ir paralēla taisnei Dota funkcija– 6Dota funkcija– 11, tad tā slīpums ir vienāds ar 2, t.i. ( Dota funkcija 0) = 2. Atradīsim šo abscisu no nosacījuma, ka 3 Dota funkcija 0 + 2 = 2. Šī vienlīdzība ir spēkā tikai tad, ja 1. piemērs.(Dota funkcija 0 = 0 un plkst Tad = 2Dota funkcija + 0 = 2. Tā kā abos gadījumos 0) = 5, tad taisni

b 0 = 2. Tā kā abos gadījumos pieskaras funkcijas grafikam vai nu punktā (0; 5), vai punktā (2; 5). 0 = 2. Tā kā abos gadījumos Pirmajā gadījumā skaitliskā vienādība 5 = 2×0 + ir patiesa 0 = 2. Tā kā abos gadījumos pieskaras funkcijas grafikam vai nu punktā (0; 5), vai punktā (2; 5). 0 = 2. Tā kā abos gadījumos = 1.

, kur Tad = 2Dota funkcija= 5, un otrajā gadījumā skaitliskā vienādība 5 = 2×2 + ir patiesa Tad = 2Dota funkcija Tātad ir divas pieskares 1. piemērs.(Dota funkcija+ 5 un + 5. Uzrakstīsim funkcijas grafika pieskares vienādojumu = 2Dota funkcija – 11.

0) = = 10. Pieskares vienādojumam ir šāda forma: Tad = 2Dota funkcija + 5, Tad = 2Dota funkcija + 1.

+ 1 funkcijas grafikam– M., Maskavas Valsts universitāte, 1968. 1. piemērs.(Dota funkcija) = Dota funkcija 2 – 6Dota funkcija), paralēli līnijai 1. piemērs.(Dota funkcija 3. piemērs. + 7. Uzrakstīsim funkcijas grafika pieskares vienādojumu (2; –5).

Risinājums.), kas iet caur punktu 1. piemērs. A + 7. Uzrakstīsim funkcijas grafika pieskares vienādojumu Jo 1. piemērs.(Dota funkcija(2) –5, tad punkts Dota funkcija nepieder pie funkcijas grafika

). Ļaujiet 1. piemērs.(Dota funkcija) grafika punktā ar abscisu Funkcijas atvasinājums ) pastāv jebkuram x

= (Dota funkcija 2 – 6Dota funkcija 0 - pieskares punkta abscisa. Dota funkcija – 6.

. Atradīsim viņu: 1. piemērs.(Dota funkcija 0) = Dota funkcija– 6Dota funkcija 0 + 7; (Dota funkcija 0) = 2Dota funkcija Funkcijas atvasinājums

Tad = (2Dota funkcija 0 – 6)(Dota funkcija – Dota funkcija 0) + Dota funkcija– 6Dota funkcija+ 7,

Tad = (2Dota funkcija 0 – 6)Dota funkcija– Dota funkcija+ 7.

+ 1)′ = 2 + 7. Uzrakstīsim funkcijas grafika pieskares vienādojumu 0 – 6. Pieskares vienādojumam ir šāda forma:

–5 = (2Dota funkcija Kopš punkta Dota funkcija+ 7,

pieder pie tangensa, tad skaitliskā vienādība ir patiesa Dota funkcija 0–6) × 2– Dota funkcija kur + 7. Uzrakstīsim funkcijas grafika pieskares vienādojumu 0 = 0 vai 1. piemērs.(Dota funkcija).

0 = 4. Tas nozīmē, ka caur punktu Dota funkcija funkcijas grafikam var uzzīmēt divas pieskares Tad = –6Dota funkcija Ja Dota funkcija 0 = 0, tad pieskares vienādojumam ir forma Tad = 2Dota funkcija – 9.

0) = = 10. Pieskares vienādojumam ir šāda forma: Tad = –6Dota funkcija + 7, Tad = 2Dota funkcija – 9.

+ 7. Ja 0 = 4, tad pieskares vienādojumam ir forma 1. piemērs.(Dota funkcija) = Dota funkcija 2 – 2Dota funkcija 4. piemērs. Dotās funkcijas(Dota funkcija) = –Dota funkcija+ 2 un

Risinājums. g Dota funkcija 2 – 3. Uzrakstīsim šo funkciju grafikos kopējās pieskares vienādojumu. 1. piemērs.(Dota funkcijaĻaujiet Dota funkcija 1 - vajadzīgās līnijas pieskares punkta abscisa ar funkcijas grafiku Dotās funkcijas(Dota funkcija).

). Ļaujiet 1. piemērs.(Dota funkcija) grafika punktā ar abscisu Funkcijas atvasinājums ) pastāv jebkuram x

= (Dota funkcija 2 – 2Dota funkcija), A Dota funkcija – 2.

. Atradīsim viņu: 1. piemērs.(Dota funkcija 1) = Dota funkcija– 2Dota funkcija 1 + 2; (Dota funkcija 1) = 22 - tās pašas līnijas pieskares punkta abscisa ar funkcijas grafiku+ 2)′ = 2

Tad = (2Dota funkcija 1 – 2)(Dota funkcija – Dota funkcija 1) + Dota funkcija– 2Dota funkcija 1 + 2,

+ 5. Uzrakstīsim funkcijas grafika pieskares vienādojumu = (2Dota funkcija 1 – 2)Dota funkcija – Dota funkcija+ 2. (1)

x Dotās funkcijas(Dota funkcija):

= (–Dota funkcija 1 – 2. Pieskares vienādojumam ir šāda forma: Dota funkcija.

Atradīsim funkcijas atvasinājumu

2 – 3)′ = –2

1. Dota funkcija f, kurai kādā punktā x 0 ir galīgs atvasinājums f (x 0). Tad taisni, kas iet caur punktu (x 0 ; f (x 0)) ar leņķa koeficientu f ’(x 0), sauc par pieskari.
2. Kas notiek, ja atvasinājums neeksistē punktā x 0? Ir divas iespējas:

Nav arī pieskares grafikam. Klasisks piemērs ir funkcija y = |x | punktā (0; 0).

Jebkura nevertikāla taisne tiek dota ar vienādojumu formā y = kx + b, kur k ir slīpums. Pieskares nav izņēmums, un, lai izveidotu tā vienādojumu kādā punktā x 0, šajā punktā pietiek zināt funkcijas un atvasinājuma vērtību.

Tātad ir dota funkcija y = f (x), kurai segmentā ir atvasinājums y = f ’(x). Tad jebkurā punktā x 0 ∈ (a ; b) šīs funkcijas grafikam var uzvilkt tangensu, kas tiek dota ar vienādojumu:

y = f ’(x 0) (x − x 0) + f (x 0)

Šeit f ’(x 0) ir atvasinājuma vērtība punktā x 0, un f (x 0) ir pašas funkcijas vērtība.

Uzdevums. Dota funkcija y = x 3 . Uzrakstiet vienādojumu šīs funkcijas grafika pieskarei punktā x 0 = 2.

Pieskares vienādojums: y = f ’(x 0) · (x − x 0) + f (x 0). Punkts x 0 = 2 mums ir dots, bet būs jāaprēķina vērtības f (x 0) un f ’(x 0).

Vispirms noskaidrosim funkcijas vērtību. Šeit viss ir vienkārši: f (x 0) = f (2) = 2 3 = 8;
Tagad atradīsim atvasinājumu: f '(x) = (x 3)' = 3x 2;
Mēs aizstājam x 0 = 2 atvasinājumā: f ’(x 0) = f ’(2) = 3 2 2 = 12;
Kopumā mēs iegūstam: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Šis ir pieskares vienādojums.

Uzdevums. Uzrakstiet vienādojumu funkcijas f (x) = 2sin x + 5 grafika pieskarei punktā x 0 = π /2.

Šoreiz mēs sīkāk neaprakstīsim katru darbību – norādīsim tikai galvenos soļus. Mums ir:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f '(x) = (2sin x + 5)' = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Pieskares vienādojums:

y = 0 · (x − π /2) + 7 ⇒ y = 7

Pēdējā gadījumā taisnā līnija izrādījās horizontāla, jo tā leņķiskais koeficients k = 0. Tam nav nekā slikta – mēs tikko uzdūrāmies ekstrēma punktam.

Tangenss ir taisna līnija , kas pieskaras funkcijas grafikam vienā punktā un kuras visi punkti atrodas mazākajā attālumā no funkcijas grafika. Tāpēc pieskares pieskares pieskaras funkcijas grafikam noteiktā leņķī, un vairākas pieskares dažādos leņķos nevar iziet cauri pieskares punktam. Funkcijas grafika pieskares vienādojumi un normālie vienādojumi tiek konstruēti, izmantojot atvasinājumu.

Pieskares vienādojums ir iegūts no līnijas vienādojuma .

Atvasināsim pieskares vienādojumu un pēc tam normas vienādojumu funkcijas grafikam.

Tad = kx + 0 = 2. Tā kā abos gadījumos .

Tajā k- leņķa koeficients.

No šejienes mēs saņemam šādu ierakstu:

Tad - Tad 0 = k(Dota funkcija - Dota funkcija 0 ) .

Atvasinātā vērtība 1. piemērs. "(Dota funkcija 0 ) funkcijas Tad = 1. piemērs.(Dota funkcija) punktā Dota funkcija0 vienāds slīpums k= tg φ pieskares funkcijas grafikam, kas novilkta caur punktu M0 (Dota funkcija 0 , Tad 0 ) , Kur Tad0 = 1. piemērs.(Dota funkcija 0 ) . Tas ir ģeometriskā nozīme atvasinājums .

Tādējādi mēs varam aizstāt k ieslēgts 1. piemērs. "(Dota funkcija 0 ) un iegūstiet tālāk norādīto funkcijas grafika pieskares vienādojums :

Tad - Tad 0 = 1. piemērs. "(Dota funkcija 0 )(Dota funkcija - Dota funkcija 0 ) .

Problēmās, kas saistītas ar funkcijas grafika pieskares vienādojuma sastādīšanu (un mēs drīz pāriesim pie tiem), vienādojums, kas iegūts no iepriekš minētās formulas, ir jāsamazina līdz taisnas līnijas vienādojums vispārīgā formā. Lai to izdarītu, visi burti un cipari ir jāpārvieto uz vienādojuma kreiso pusi, bet labajā pusē jāatstāj nulle.

Tagad par parasto vienādojumu. Normāls - tā ir taisne, kas iet caur pieskares punktu funkcijas grafikam, kas ir perpendikulāra pieskarei. Normāls vienādojums :

(Dota funkcija - Dota funkcija 0 ) + 1. piemērs. "(Dota funkcija 0 )(Tad - Tad 0 ) = 0

Lai iesildītos, jums pašam jāatrisina pirmais piemērs un pēc tam jāskatās uz risinājumu. Ir pamats cerēt, ka šis uzdevums mūsu lasītājiem nebūs “aukstā duša”.

0. piemērs. Izveidojiet pieskares vienādojumu un normālo vienādojumu funkcijas grafikam punktā M (1, 1) .

/ Red. P.Ya. Galperiņa, N.F. Taļizina. Uzrakstiet pieskares vienādojumu un normālo vienādojumu funkcijas grafikam , ja abscisa ir tangenss .

Atradīsim funkcijas atvasinājumu:

Tagad mums ir viss, kas jāievieto teorētiskajā palīdzībā, lai iegūtu tangentes vienādojumu. Mēs saņemam

Šajā piemērā mums paveicās: slīpums izrādījās nulle, tāpēc mēs atsevišķi samazinām vienādojumu līdz vispārējais izskats nebija vajadzīgs. Tagad mēs varam izveidot normālu vienādojumu:

Attēlā zemāk: funkcijas grafiks bordo krāsā, tangenss zaļš, oranžs normāls.

Nākamais piemērs arī nav sarežģīts: funkcija, tāpat kā iepriekšējā, ir arī polinoms, bet slīpums nebūs vienāds ar nulli, tāpēc tiks pievienots vēl viens solis - vienādojuma nogādāšana vispārējā formā.

y

Risinājums. Atradīsim pieskares punkta ordinātas:

Atradīsim funkcijas atvasinājumu:

.

Atradīsim atvasinājuma vērtību pieskares punktā, tas ir, pieskares slīpumu:

Mēs aizvietojam visus iegūtos datus “tukšā formulā” un iegūstam tangensvienādojumu:

Mēs izveidojam vienādojumu tā vispārējā formā (kreisajā pusē apkopojam visus burtus un ciparus, izņemot nulli, un labajā pusē atstājam nulli):

Mēs sastādām normālo vienādojumu:

+ 1 funkcijas grafikam Uzrakstiet pieskares vienādojumu un normas vienādojumu funkcijas grafikam, ja abscisa ir pieskares punkts.

Risinājums. Atradīsim pieskares punkta ordinātas:

Atradīsim funkcijas atvasinājumu:

.

Atradīsim atvasinājuma vērtību pieskares punktā, tas ir, pieskares slīpumu:

.

Mēs atrodam tangentes vienādojumu:

Pirms vienādojuma vispārējā formā tas ir nedaudz “ķemmēts”: reiziniet terminu ar 4. Mēs to darām un vienādojumu iegūstam tā vispārējā formā:

Mēs sastādām normālo vienādojumu:

+ 7. Ja Uzrakstiet pieskares vienādojumu un normas vienādojumu funkcijas grafikam, ja abscisa ir pieskares punkts.

Risinājums. Atradīsim pieskares punkta ordinātas:

.

Atradīsim funkcijas atvasinājumu:

Atradīsim atvasinājuma vērtību pieskares punktā, tas ir, pieskares slīpumu:

.

Mēs iegūstam tangentes vienādojumu:

Mēs izveidojam vienādojumu tā vispārējā formā:

Mēs sastādām normālo vienādojumu:

Izplatīta kļūda, rakstot pieskares un normālos vienādojumus, ir nepamanīt, ka piemērā dotā funkcija ir sarežģīta, un aprēķināt tās atvasinājumu kā vienkāršas funkcijas atvasinājumu. Tālāk minētie piemēri jau ir no sarežģītas funkcijas(attiecīgā nodarbība tiks atvērta jaunā logā).

5. piemērs. Uzrakstiet pieskares vienādojumu un normas vienādojumu funkcijas grafikam, ja abscisa ir pieskares punkts.

Risinājums. Atradīsim pieskares punkta ordinātas:

Uzmanību! Šī funkcija ir sarežģīta, jo pieskares arguments (2 Dota funkcija) pati par sevi ir funkcija. Tāpēc funkcijas atvasinājumu mēs atrodam kā kompleksās funkcijas atvasinājumu.

Y = f(x) un, ja šajā punktā funkcijas grafikam var uzzīmēt pieskari, kas nav perpendikulāra abscisu asij, tad pieskares leņķiskais koeficients ir vienāds ar f"(a). Mēs jau esam izdarījuši izmantoja to vairākas reizes, piemēram, 33. paragrāfā tika konstatēts, ka funkcijas y = sin x (sinusoīda) grafiks veido 45° leņķi ar x asi (precīzāk, pieskares pieskarei). grafiks sākuma punktā veido 45° leņķi ar x ass pozitīvo virzienu), un 5. piemērā tika atrasti 33 punkti saskaņā ar doto grafiku. funkcijas, kurā pieskare ir paralēla x asij. 33.§ 2.piemērā tika sastādīts vienādojums funkcijas y = x 2 grafika pieskarei punktā x = 1 (precīzāk, punktā (1; 1), bet biežāk ir tikai abscisu vērtība). norādīts, uzskatot, ka, ja ir zināma abscisu vērtība, tad ordinātu vērtību var atrast no vienādojuma y = f(x)). Šajā sadaļā mēs izstrādāsim algoritmu jebkuras funkcijas grafikam pieskares vienādojuma sastādīšanai.

Dota funkcija y = f(x) un punkts M (a; f(a)), kā arī zināms, ka eksistē f"(a). Izveidosim vienādojumu grafa pieskarei dotā funkcija noteiktā punktā. Šim vienādojumam, tāpat kā jebkuras taisnes vienādojumam, kas nav paralēla ordinātu asij, ir forma y = kx+m, tāpēc uzdevums ir atrast koeficientu k un m vērtības.

Ar leņķisko koeficientu k nav problēmu: mēs zinām, ka k = f "(a). Lai aprēķinātu m vērtību, mēs izmantojam faktu, ka vēlamā taisne iet caur punktu M(a; f (a)) Tas nozīmē, ka, aizvietojot koordinātas punktu M taisnes vienādojumā, mēs iegūstam pareizo vienādību: f(a) = ka+m, no kuras mēs secinām, ka m = f(a) - ka.
Atliek aizstāt atrastās komplekta koeficientu vērtības vienādojums tiešs:

Esam ieguvuši vienādojumu funkcijas y = f(x) grafika pieskarei punktā x=a.
Ja, teiksim,
Aizvietojot atrastās vērtības a = 1, f(a) = 1 f"(a) = 2 vienādojumā (1), iegūstam: y = 1+2(x-f), t.i., y = 2x-1.
Salīdziniet šo rezultātu ar rezultātu, kas iegūts 2. piemērā no 33. §. Protams, notika tas pats.
Izveidosim vienādojumu funkcijas y = tan x grafika pieskarei sākuma punktā. Mums ir: tas nozīmē cos x f"(0) = 1. Aizvietojot atrastās vērtības a = 0, f(a) = 0, f"(a) = 1 vienādojumā (1), iegūstam: y = x.
Tāpēc mēs zīmējām tangentoīdu § 15 (sk. 62. att.) caur koordinātu sākumpunktu 45° leņķī pret abscisu asi.
Atrisinot šos pietiekami vienkāršus piemērus, mēs faktiski izmantojām noteiktu algoritmu, kas ir ietverts formulā (1). Padarīsim šo algoritmu skaidru.

ALGORITMS FUNKCIJAS y = f(x) GRAFIKA TANGENTA IZSTRĀDĀŠANAI

1) Pieskares punkta abscisu apzīmē ar burtu a.
2) Aprēķiniet 1 (a).
3) Atrodiet f"(x) un aprēķiniet f"(a).
4) Atrastos skaitļus a, f(a), (a) aizstājiet formulā (1).

/ Red. P.Ya. Galperiņa, N.F. Taļizina. Uzrakstiet vienādojumu pieskarei funkcijas grafikam punktā x = 1.
Izmantosim algoritmu, ņemot vērā to, ka in šajā piemērā

Attēlā 126 ir attēlota hiperbola, konstruēta taisne y = 2.
Zīmējums apstiprina iepriekš minētos aprēķinus: tiešām, līnija y = 2 skar hiperbolu punktā (1; 1).

Atbilde: y = 2-x.
y Funkcijas grafikam uzzīmējiet pieskari tā, lai tā būtu paralēla taisnei y = 4x - 5.
Precizēsim problēmas formulējumu. Prasība "uzzīmēt pieskares" parasti nozīmē "veidot vienādojumu pieskarei". Tas ir loģiski, jo, ja cilvēks varēja izveidot vienādojumu pieskarei, tad viņam, izmantojot tās vienādojumu, diez vai būs grūtības izveidot taisnu līniju koordinātu plaknē.
Izmantosim pieskares vienādojuma sastādīšanas algoritmu, ņemot vērā, ka šajā piemērā Bet atšķirībā no iepriekšējā piemēra ir neskaidrības: pieskares punkta abscisa nav skaidri norādīta.
Sāksim domāt šādi. Vēlamajai pieskarei jābūt paralēlai taisnei y = 4x-5. Divas taisnes ir paralēlas tad un tikai tad, ja to slīpumi ir vienādi. Tas nozīmē, ka pieskares leņķa koeficientam jābūt vienādam ar dotās taisnes leņķa koeficientu: Tādējādi mēs varam atrast a vērtību no vienādojuma f"(a) = 4.
Mums ir:
No vienādojuma Tas nozīmē, ka ir divas pieskares, kas atbilst uzdevuma nosacījumiem: viena punktā ar abscisu 2, otra punktā ar abscisu -2.
Tagad jūs varat sekot algoritmam.

+ 1 funkcijas grafikam No punkta (0; 1) uzzīmējiet pieskares funkcijas grafikam
Izmantosim pieskares vienādojuma sastādīšanas algoritmu, ņemot vērā, ka šajā piemērā Ņemiet vērā, ka šeit, tāpat kā 2. piemērā, pieskares punkta abscisa nav skaidri norādīta. Tomēr mēs sekojam algoritmam.

Pēc nosacījuma pieskare iet caur punktu (0; 1). Aizvietojot vērtības x = 0, y = 1 vienādojumā (2), mēs iegūstam:
Kā redzat, šajā piemērā tikai algoritma ceturtajā solī mums izdevās atrast pieskares punkta abscisu. Aizvietojot vērtību a =4 vienādojumā (2), mēs iegūstam:

Attēlā 127 attēlo aplūkotā piemēra ģeometrisku ilustrāciju: tiek uzzīmēts funkcijas grafiks

32. paragrāfā mēs atzīmējām, ka funkcijai y = f(x), kurai ir atvasinājums fiksētā punktā x, ir spēkā aptuvenā vienādība:

Turpmākās argumentācijas ērtībai mainīsim apzīmējumu: x vietā rakstīsim a, tā vietā rakstīsim x un attiecīgi rakstīsim x-a. Tad iepriekš uzrakstītā aptuvenā vienādība būs šāda:

Tagad apskatiet att. 128. Funkcijas y = f(x) grafikam punktā M (a; f (a)) uzzīmēta pieskare. Punkts x ir atzīmēts uz x ass tuvu a. Ir skaidrs, ka f(x) ir funkcijas in grafika ordināta norādītais punkts X. Kas ir f(a) + f"(a) (x-a)? Šī ir pieskares ordināta, kas atbilst vienam un tam pašam punktam x - skatiet formulu (1). Ko nozīmē aptuvenā vienādība (3)? Fakts ka Lai aprēķinātu funkcijas aptuveno vērtību, ņem pieskares ordinātu vērtību.

+ 7. Ja Atrodiet aptuveno vērtību skaitliskā izteiksme 1,02 7 .
Runa ir par par funkcijas y = x 7 vērtības atrašanu punktā x = 1.02. Izmantosim formulu (3), ņemot vērā to šajā piemērā
Rezultātā mēs iegūstam:

Ja mēs izmantojam kalkulatoru, mēs iegūstam: 1,02 7 = 1,148685667...
Kā redzat, tuvinājuma precizitāte ir diezgan pieņemama.
Atbilde: 1,02 7 =1,14.

A.G. Mordkoviča algebra 10. klase

Kalendāra tematiskā plānošana matemātikā, video matemātikā tiešsaistē, matemātika skolā lejupielādēt

Nodarbības saturs nodarbību piezīmes atbalsta ietvarstundu prezentācijas paātrināšanas metodes interaktīvās tehnoloģijas Prakse uzdevumi un vingrinājumi pašpārbaudes darbnīcas, apmācības, gadījumi, uzdevumi mājasdarbi diskusijas jautājumi retoriski jautājumi no studentiem Ilustrācijas audio, video klipi un multivide fotogrāfijas, attēli, grafikas, tabulas, diagrammas, humors, anekdotes, joki, komiksi, līdzības, teicieni, krustvārdu mīklas, citāti Papildinājumi tēzes raksti triki zinātkārajiem bērnu gultiņas mācību grāmatas pamata un papildu terminu vārdnīca citi Mācību grāmatu un stundu pilnveidošanakļūdu labošana mācību grāmatā fragmenta atjaunināšana mācību grāmatā, inovācijas elementi stundā, novecojušo zināšanu aizstāšana ar jaunām Tikai skolotājiem ideālas nodarbības kalendārais plāns gadam metodiskie ieteikumi diskusiju programmas Integrētās nodarbības