Løs lineær matriseligning. invers matrise

La oss få et system av lineære ligninger med ukjent:

Vi vil anta at hovedmatrisen ikke-degenerert. Så, ved teorem 3.1, eksisterer det en invers matrise
Multiplisere matriseligningen
til matrisen
til venstre, ved å bruke definisjon 3.2, samt utsagn 8) av setning 1.1, får vi formelen som matrisemetoden for å løse systemer med lineære ligninger er basert på:

Kommentar. Legg merke til at matrisemetoden for å løse systemer med lineære ligninger, i motsetning til Gauss-metoden, har begrenset anvendelse: denne metoden kan bare løse systemer med lineære ligninger der for det første antall ukjente er lik antall ligninger, og for det andre er hovedmatrisen ikke-entall.

Eksempel. Løs et system med lineære ligninger ved å bruke matrisemetoden.

Et system med tre lineære ligninger med tre ukjente er gitt
Hvor

Hovedmatrisen til ligningssystemet er ikke-entall, siden dens determinant er ikke-null:

Invers matrise
La oss komponere ved å bruke en av metodene beskrevet i avsnitt 3.

Ved å bruke formelen til matrisemetoden for å løse systemer med lineære ligninger får vi

5.3. Cramer metode

Denne metoden, som matrisemetoden, er kun anvendelig for systemer med lineære ligninger der antall ukjente faller sammen med antall ligninger. Cramers metode er basert på teoremet med samme navn:

Teorem 5.2. System lineære ligninger med ukjent

hvis hovedmatrise er ikke-entall, har en unik løsning som kan oppnås ved hjelp av formlene

Hvor
determinant for en matrise avledet fra basismatrisen ligningssystem ved å erstatte det
kolonne med en kolonne med gratis medlemmer.

Eksempel. La oss finne løsningen på systemet med lineære ligninger som ble vurdert i forrige eksempel ved å bruke Cramers metode. Hovedmatrisen til ligningssystemet er ikke-degenerert, siden
La oss beregne determinantene



Ved å bruke formlene presentert i teorem 5.2, beregner vi verdiene til de ukjente:

6. Studie av lineære ligningssystemer.

Grunnleggende løsning

Å studere et system med lineære ligninger betyr å bestemme om dette systemet er kompatibelt eller inkompatibelt, og hvis det er kompatibelt, å finne ut om dette systemet er bestemt eller ubestemt.

Kompatibilitetsbetingelsen for et system med lineære ligninger er gitt av følgende teorem

Teorem 6.1 (Kronecker–Capelli).

Et system med lineære ligninger er konsistent hvis og bare hvis rangeringen til hovedmatrisen til systemet er lik rangeringen til den utvidede matrisen:

For et simultant system av lineære ligninger løses spørsmålet om dets bestemthet eller usikkerhet ved å bruke følgende teoremer.

Teorem 6.2. Hvis rangeringen av hovedmatrisen til et felles system er lik antall ukjente, så er systemet bestemt

Teorem 6.3. Hvis rangeringen av hovedmatrisen til et felles system er mindre enn antall ukjente, er systemet usikkert.

Fra de formulerte teoremene følger således en metode for å studere systemer med lineære algebraiske ligninger. La n– antall ukjente,

Deretter:


Definisjon 6.1. Den grunnleggende løsningen til et ubestemt system av lineære ligninger er en løsning der alle frie ukjente er lik null.

Eksempel. Utforsk et system med lineære ligninger. Hvis systemet er usikkert, finn den grunnleggende løsningen.

La oss beregne rekkene til de viktigste og utvidede matriser av dette ligningssystemet, som vi bringer den utvidede (og samtidig hovedmatrisen til systemet til en trinnvis form:

Legg til den andre raden i matrisen til dens første rad, multiplisert med tredje linje - med første linje multiplisert med
og den fjerde linjen - med den første, multiplisert med vi får en matrise

Til den tredje raden i denne matrisen legger vi den andre raden multiplisert med
og til den fjerde linjen – den første, multiplisert med
Som et resultat får vi matrisen

fjerne den tredje og fjerde raden som vi får en trinnmatrise fra

Dermed,

Følgelig er dette systemet med lineære ligninger konsistent, og siden rangeringsverdien er mindre enn antall ukjente, er systemet usikkert. Trinnmatrisen som oppnås som et resultat av elementære transformasjoner tilsvarer ligningssystemet

Ukjent Og er de viktigste, og de ukjente Og
gratis. Ved å tilordne nullverdier til de frie ukjente, får vi en grunnleggende løsning på dette lineære ligningssystemet.

Et system av m lineære ligninger med n ukjente kalt et formsystem

Hvor en ij Og b i (Jeg=1,…,m; b=1,…,n) er noen kjente tall, og x 1,...,x n– ukjent. I betegnelsen av koeffisienter en ij første indeks Jeg angir ligningsnummeret, og det andre j– nummeret på de ukjente som denne koeffisienten står på.

Vi vil skrive koeffisientene for de ukjente i form av en matrise 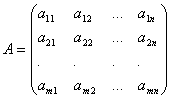, som vi kaller matrise av systemet.

Tallene på høyre side av ligningene er b 1,...,b m er kalt gratis medlemmer.

Totalitet n tall c 1,...,c n kalt beslutning av et gitt system, hvis hver likning i systemet blir en likhet etter å ha erstattet tall i den c 1,...,c n i stedet for de tilsvarende ukjente x 1,...,x n.

Vår oppgave blir å finne løsninger på systemet. I dette tilfellet kan tre situasjoner oppstå:

Et system med lineære ligninger som har minst én løsning kalles ledd. Ellers, dvs. hvis systemet ikke har noen løsninger, kalles det ikke-ledd.

La oss vurdere måter å finne løsninger på systemet på.


MATRISKEMETODE FOR LØSE SYSTEMER AV LINEÆRE LIGNINGER

Matriser gjør det mulig å kort skrive ned et system med lineære ligninger. La et system med 3 ligninger med tre ukjente gis:

Tenk på systemmatrisen 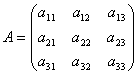og matriser kolonner med ukjente og frie termer

La oss finne arbeidet

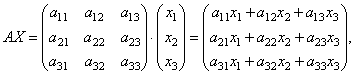
de. som et resultat av produktet får vi venstre side av likningene til dette systemet. Deretter, ved å bruke definisjonen av matriselikhet, kan dette systemet skrives i skjemaet

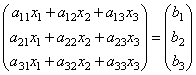eller kortere EN∙X=B.

Her er matrisene EN Og B er kjent, og matrisen X ukjent. Det er nødvendig å finne det, fordi... dens elementer er løsningen på dette systemet. Denne ligningen kalles matriseligning.

La determinanten til matrisen være forskjellig fra null | EN| ≠ 0. Da løses matriseligningen som følger. Multipliser begge sider av ligningen til venstre med matrisen A-1, invers av matrisen EN: . Fordi det A -1 A = E Og E∙X = X, så får vi en løsning på matriseligningen i formen X = A -1 B .

Merk at siden den inverse matrisen bare kan finnes for kvadratiske matriser, kan matrisemetoden bare løse de systemene der antall ligninger sammenfaller med antall ukjente. Imidlertid er matriseregistrering av systemet også mulig i tilfellet når antall ligninger ikke er lik antall ukjente, da matrisen EN vil ikke være firkantet og derfor er det umulig å finne en løsning på systemet i skjemaet X = A -1 B.

Eksempler. Løse ligningssystemer.

CRAMERS REGEL

Tenk på et system med 3 lineære ligninger med tre ukjente:

Tredjeordens determinant som tilsvarer systemmatrisen, dvs. sammensatt av koeffisienter for ukjente,

kalt determinant for systemet.

La oss komponere ytterligere tre determinanter som følger: erstatte sekvensielt 1, 2 og 3 kolonner i determinanten D med en kolonne med frie termer

Da kan vi bevise følgende resultat.

Teorem (Cramers regel). Hvis determinanten til systemet Δ ≠ 0, så har systemet som vurderes én og bare én løsning, og

Bevis. Så la oss vurdere et system med 3 ligninger med tre ukjente. La oss multiplisere den første ligningen i systemet med det algebraiske komplementet A 11 element en 11, 2. ligning – på A 21 og 3. – på A 31:

La oss legge til disse ligningene:

La oss se på hver av parentesene og høyre side av denne ligningen. Ved teoremet om utvidelse av determinanten i elementer i 1. kolonne

På samme måte kan det vises at og .

Til slutt er det lett å legge merke til det

Dermed oppnår vi likheten: .

Derfor,.

Likhetene og er avledet på samme måte, hvorfra setningen til teoremet følger.

Dermed legger vi merke til at hvis determinanten til systemet Δ ≠ 0, så har systemet en unik løsning og omvendt. Hvis determinanten til systemet er lik null, så har systemet enten et uendelig antall løsninger eller har ingen løsninger, dvs. uforenlig.

Eksempler. Løs ligningssystem


GAUSS-METODEN

De tidligere diskuterte metodene kan brukes til å løse bare de systemene der antall ligninger sammenfaller med antall ukjente, og determinanten til systemet må være forskjellig fra null. Gauss-metoden er mer universell og egnet for systemer med et hvilket som helst antall ligninger. Den består i konsekvent eliminering av ukjente fra systemets ligninger.

Vurder igjen et system med tre ligninger med tre ukjente:

.

Vi vil la den første ligningen være uendret, og fra den andre og tredje vil vi ekskludere termene som inneholder x 1. For å gjøre dette, del den andre ligningen med EN 21 og gang med – EN 11, og legg den deretter til den første ligningen. På samme måte deler vi den tredje ligningen med EN 31 og gang med – EN 11, og legg den deretter til med den første. Som et resultat vil det opprinnelige systemet ha formen:

Nå fra den siste ligningen eliminerer vi begrepet som inneholder x 2. For å gjøre dette, del den tredje ligningen med, multipliser med og legg til med den andre. Da vil vi ha et ligningssystem:

Herfra, fra den siste ligningen er det lett å finne x 3, deretter fra 2. ligning x 2 og til slutt, fra 1. x 1.

Ved bruk av Gauss-metoden kan likningene byttes om nødvendig.

Ofte, i stedet for å skrive et nytt ligningssystem, begrenser de seg til å skrive ut den utvidede matrisen til systemet:

og deretter bringe den til en trekantet eller diagonal form ved hjelp av elementære transformasjoner.

TIL elementære transformasjoner matriser inkluderer følgende transformasjoner:

  1. omorganisere rader eller kolonner;
  2. multiplisere en streng med et annet tall enn null;
  3. legge til andre linjer på en linje.

Eksempler: Løs ligningssystemer ved hjelp av Gauss-metoden.


Dermed har systemet et uendelig antall løsninger.

  • 6.4. Noen applikasjoner av dot-produktet
  • 11. Uttrykk av skalarproduktet til en vektor gjennom koordinatene til faktorene. Teorem.
  • 12. Lengde på en vektor, lengde på et segment, vinkel mellom vektorer, tilstand for vinkelrett til vektorer.
  • 13. Vektorprodukt av vektorer, dets egenskaper. Arealet av et parallellogram.
  • 14. Blandet produkt av vektorer, dets egenskaper. Betingelse for vektorkoplanaritet. Volum av et parallellepiped. Volum av pyramiden.
  • 15. Metoder for å definere en rett linje på et plan.
  • 16. Normalligning av en linje på et plan (avledning). Geometrisk betydning av koeffisienter.
  • 17. Ligning av en rett linje på et plan i segmenter (avledning).
  • Redusere den generelle ligningen til planet til ligningen til planet i segmenter.
  • 18. Ligning av en rett linje på et plan med en vinkelkoeffisient (avledning).
  • 19. Ligning av en rett linje på et plan som går gjennom to punkter (avledning).
  • 20. Vinkel mellom rette linjer på et plan (utgang).
  • 21. Avstand fra et punkt til en rett linje på et plan (utgang).
  • 22. Betingelser for parallellitet og perpendikularitet av linjer på et plan (avledning).
  • 23. Ligning av et plan. Normalplanligning (avledning). Geometrisk betydning av koeffisienter.
  • 24. Ligning av et plan i segmenter (avledning).
  • 25. Ligning av et plan som går gjennom tre punkter (derivasjon).
  • 26. Vinkel mellom plan (utgang).
  • 27. Avstand fra et punkt til et plan (utgang).
  • 28. Betingelser for parallellitet og perpendikularitet av plan (konklusjon).
  • 29. Ligninger av en linje i r3. Ligninger av en linje som går gjennom to faste punkter (avledning).
  • 30. Kanoniske ligninger av en rett linje i rommet (avledning).
  • Tegne kanoniske ligninger av en rett linje i rommet.
  • Spesielle tilfeller av kanoniske ligninger av en rett linje i rommet.
  • Kanoniske ligninger av en linje som går gjennom to gitte punkter i rommet.
  • Overgang fra de kanoniske ligningene til en linje i rommet til andre typer ligninger av en linje.
  • 31. Vinkel mellom rette linjer (utgang).
  • 32. Avstand fra et punkt til en rett linje på et plan (utgang).
  • Avstand fra et punkt til en rett linje på et plan - teori, eksempler, løsninger.
  • Den første måten å finne avstanden fra et gitt punkt til en gitt rett linje på et plan.
  • Den andre metoden lar deg finne avstanden fra et gitt punkt til en gitt rett linje på et plan.
  • Løse problemer med å finne avstanden fra et gitt punkt til en gitt rett linje på et plan.
  • Avstand fra et punkt til en linje i rommet - teori, eksempler, løsninger.
  • Den første måten å finne avstanden fra et punkt til en linje i rommet.
  • Den andre metoden lar deg finne avstanden fra et punkt til en linje i rommet.
  • 33. Betingelser for parallellitet og perpendikularitet av linjer i rommet.
  • 34. Den relative plasseringen av linjer i rommet og en linje med et plan.
  • 35. Klassisk ellipseligning (avledning) og dens konstruksjon. Den kanoniske ligningen til en ellipse har formen hvor er positive reelle tall, og hvordan konstruere en ellipse?
  • 36. Klassisk hyperbelligning (avledning) og dens konstruksjon. Asymptoter.
  • 37. Kanonisk parabelligning (avledning) og konstruksjon.
  • 38. Funksjon. Grunnleggende definisjoner. Grafer over grunnleggende elementære funksjoner.
  • 39. Tallrekker. Begrensning av tallrekkefølge.
  • 40. Uendelig små og uendelig store mengder. Teorem om sammenhengen mellom dem, egenskaper.
  • 41. Teoremer om handlinger på variabler som har endelige grenser.
  • 42. Nummer e.
  • Innhold
  • Bestemmelsesmetoder
  • Egenskaper
  • Historie
  • Approksimasjoner
  • 43. Bestemmelse av grensen for en funksjon. Avdekke usikkerheter.
  • 44. Bemerkelsesverdige grenser, deres konklusjon. Ekvivalente uendelige mengder.
  • Innhold
  • Den første fantastiske grensen
  • Andre fantastiske grense
  • 45. Ensidige grenser. Kontinuitet og diskontinuiteter av funksjon. Ensidige grenser
  • Venstre og høyre grenser for en funksjon
  • Diskontinuitetspunkt av den første typen
  • Diskontinuitetspunkt av den andre typen
  • Avtakbart knekkpunkt
  • 46. ​​Definisjon av derivat. Geometrisk betydning, mekanisk betydning av avledet. Tangent- og normalligninger for en kurve og et punkt.
  • 47. Teoremer om den deriverte av inverse, komplekse funksjoner.
  • 48. Derivater av de enkleste elementære funksjonene.
  • 49. Differensiering av parametriske, implisitte og makteksponentielle funksjoner.
  • 21. Differensiering av implisitte og parametrisk definerte funksjoner
  • 21.1. Implisitt funksjon
  • 21.2. Parametrisk definert funksjon
  • 50. Høyere ordens derivater. Taylors formel.
  • 51. Differensial. Anvendelse av differensial til omtrentlige beregninger.
  • 52. Teoremer av Rolle, Lagrange, Cauchy. L'Hopitals regel.
  • 53. Teorem om nødvendige og tilstrekkelige betingelser for monotonisiteten til en funksjon.
  • 54. Bestemmelse av maksimum og minimum for en funksjon. Teoremer om nødvendige og tilstrekkelige betingelser for eksistensen av et ekstremum av en funksjon.
  • Teorem (nødvendig betingelse for ekstremum)
  • 55. Konveksitet og konkavitet av kurver. Bøyningspunkter. Teoremer om nødvendige og tilstrekkelige betingelser for eksistensen av bøyningspunkter.
  • Bevis
  • 57. Determinanter av n-te orden, deres egenskaper.
  • 58. Matriser og handlinger på dem. Matrix rangering.
  • Definisjon
  • Beslektede definisjoner
  • Egenskaper
  • Lineær transformasjon og matriserangering
  • 59. Invers matrise. Teorem om eksistensen av en invers matrise.
  • 60. Systemer av lineære ligninger. Matriseløsning av systemer av lineære ligninger. Cramers regel. Gauss metode. Kronecker-Capelli teorem.
  • Løse systemer av lineære algebraiske ligninger, løsningsmetoder, eksempler.
  • Definisjoner, begreper, betegnelser.
  • Løse elementære systemer av lineære algebraiske ligninger.
  • Løse systemer av lineære ligninger ved hjelp av Cramers metode.
  • Løse systemer av lineære algebraiske ligninger ved hjelp av matrisemetoden (ved å bruke en invers matrise).
  • Løse systemer av lineære ligninger ved hjelp av Gauss-metoden.
  • Løse systemer av lineære algebraiske ligninger av generell form.
  • Kronecker-Capelli-teorem.
  • Gauss-metode for å løse systemer av lineære algebraiske ligninger av generell form.
  • Skrive en generell løsning på homogene og inhomogene lineære algebraiske systemer ved å bruke vektorer av det fundamentale løsningssystemet.
  • Løse ligningssystemer som reduserer til slough.
  • Eksempler på problemer som reduserer til å løse systemer av lineære algebraiske ligninger.

    • Løse systemer av lineære algebraiske ligninger ved hjelp av matrisemetoden (ved å bruke en invers matrise).

    La systemet med lineære algebraiske ligninger gis i matriseform , hvor matrisen EN har dimensjon n på n og dens determinant er ikke null.

    Siden , da matrisen EN– er inverterbar, det vil si at det er en invers matrise. Hvis vi multipliserer begge sider av likheten til venstre, får vi en formel for å finne en matrisekolonne med ukjente variabler. Slik fikk vi en løsning på et system av lineære algebraiske ligninger ved hjelp av matrisemetoden.

    matrisemetoden.

    La oss omskrive ligningssystemet i matriseform:

    Fordi så kan SLAE løses ved hjelp av matrisemetoden. Ved å bruke den inverse matrisen kan løsningen på dette systemet finnes som .

    La oss konstruere en invers matrise ved å bruke en matrise fra algebraiske komplementer av matriseelementer EN(om nødvendig, se artikkelmetodene for å finne den inverse matrisen):

    Det gjenstår å beregne matrisen av ukjente variabler ved å multiplisere den inverse matrisen til en matrisekolonne med gratis medlemmer (se om nødvendig artikkeloperasjoner om matriser):

    eller i et annet innlegg x 1 = 4, x 2 = 0, x 3 = -1 .

    Hovedproblemet når man finner løsninger på systemer med lineære algebraiske ligninger ved bruk av matrisemetoden, er kompleksiteten ved å finne den inverse matrisen, spesielt for kvadratiske matriser av orden høyere enn tredje.

    For en mer detaljert beskrivelse av teorien og tilleggseksempler, se artikkelmatrisemetoden for løsning av systemer av lineære ligninger.

    Toppen av siden

    Løse systemer av lineære ligninger ved hjelp av Gauss-metoden.

    Anta at vi må finne en løsning på systemet fra n lineære ligninger med n ukjente variabler determinanten til hovedmatrisen som er forskjellig fra null.

    Essensen av Gauss-metoden består av sekvensiell eliminering av ukjente variabler: først eliminering x 1 fra alle likninger i systemet, fra den andre, er ytterligere ekskludert x 2 fra alle ligninger, starter med den tredje, og så videre, til bare den ukjente variabelen er igjen i den siste ligningen x n. Denne prosessen med å transformere likningene til et system for å sekvensielt eliminere ukjente variabler kalles direkte gaussisk metode. Etter å ha fullført foroverprogresjonen til Gauss-metoden, fra den siste ligningen finner vi x n, ved å bruke denne verdien fra den nest siste ligningen vi beregner x n-1, og så videre, fra den første ligningen vi finner x 1 . Prosessen med å beregne ukjente variabler når man går fra den siste ligningen i systemet til den første kalles invers av Gauss-metoden.

    La oss kort beskrive algoritmen for å eliminere ukjente variabler.

    Vi vil anta det, siden vi alltid kan oppnå dette ved å bytte ut systemets likninger. Eliminer den ukjente variabelen x 1 fra alle likninger i systemet, fra den andre. For å gjøre dette, til den andre ligningen i systemet legger vi den første, multiplisert med, til den tredje ligningen legger vi den første, multiplisert med, og så videre, til nth til ligningen legger vi den første multiplisert med. Ligningssystemet etter slike transformasjoner vil ta formen hvor og .

    Vi ville komme til samme resultat hvis vi uttrykte x 1 gjennom andre ukjente variabler i den første ligningen av systemet og det resulterende uttrykket ble erstattet med alle andre ligninger. Så variabelen x 1 ekskludert fra alle ligninger, fra den andre.

    Deretter fortsetter vi på lignende måte, men bare med en del av det resulterende systemet, som er markert i figuren

    For å gjøre dette, til den tredje ligningen i systemet legger vi den andre, multiplisert med, til den fjerde ligningen legger vi den andre, multiplisert med, og så videre, til nth til ligningen legger vi den andre, multiplisert med. Ligningssystemet etter slike transformasjoner vil ta formen hvor og . Så variabelen x 2 ekskludert fra alle ligninger fra og med den tredje.

    Deretter fortsetter vi med å eliminere det ukjente x 3 , i dette tilfellet handler vi på samme måte med den delen av systemet som er merket på figuren

    Så vi fortsetter den direkte progresjonen av Gauss-metoden til systemet tar formen

    Fra dette øyeblikket begynner vi det motsatte av Gauss-metoden: vi beregner x n fra den siste ligningen som, ved å bruke den oppnådde verdien x n Vi finner x n-1 fra nest siste ligning, og så videre, finner vi x 1 fra den første ligningen.

    Løs system av lineære ligninger Gauss metode.

    Eliminer den ukjente variabelen x 1 fra andre og tredje likning av systemet. For å gjøre dette legger vi til begge sider av den andre og tredje ligningen de tilsvarende delene av den første ligningen, multiplisert med henholdsvis og:

    La oss nå ekskludere fra den tredje ligningen x 2 , ved å legge til venstre og høyre side til venstre og høyre side av den andre ligningen, multiplisert med:

    Dette fullfører foroverslaget til Gauss-metoden.

    Fra den siste ligningen til det resulterende ligningssystemet finner vi x 3 :

    Fra den andre ligningen får vi .

    Fra den første ligningen finner vi den gjenværende ukjente variabelen og fullfører dermed det motsatte av Gauss-metoden.

    x 1 = 4, x 2 = 0, x 3 = -1 .

    For mer detaljert informasjon og flere eksempler, se avsnittet om å løse elementære systemer av lineære algebraiske ligninger ved hjelp av Gauss-metoden.

    Toppen av siden

    Denne online kalkulatoren løser et system med lineære ligninger ved hjelp av matrisemetoden. En meget detaljert løsning er gitt. For å løse et system med lineære ligninger, velg antall variabler. Velg en metode for å beregne den inverse matrisen. Skriv deretter inn dataene i cellene og klikk på "Beregn"-knappen.

    ×

    Advarsel

    Vil du fjerne alle celler?

    Lukk Slett

    Instruksjoner for dataregistrering. Tall legges inn som heltall (eksempler: 487, 5, -7623 osv.), desimaler (eks. 67., 102.54 osv.) eller brøker. Brøken må angis på formen a/b, der a og b er heltall eller desimaler. Eksempler 45/5, 6.6/76.4, -7/6.7 osv.

    Matrisemetode for å løse systemer av lineære ligninger

    Tenk på følgende system med lineære ligninger:

    Gitt definisjonen av en invers matrise, har vi EN −1 EN=E, Hvor E- identitetsmatrise. Derfor kan (4) skrives som følger:

    For å løse systemet med lineære ligninger (1) (eller (2)), er det nok å multiplisere inversen til EN matrise per begrensningsvektor b.

    Eksempler på løsning av et system med lineære ligninger ved hjelp av matrisemetoden

    Eksempel 1. Løs følgende system med lineære ligninger ved å bruke matrisemetoden:

    La oss finne inversen til matrise A ved å bruke Jordan-Gauss-metoden. På høyre side av matrisen EN La oss skrive identitetsmatrisen:

    La oss ekskludere elementene i den første kolonnen i matrisen under hoveddiagonalen. For å gjøre dette, legg til linjene 2,3 med linje 1, multiplisert med henholdsvis -1/3, -1/3:

    La oss ekskludere elementene i den andre kolonnen i matrisen under hoveddiagonalen. For å gjøre dette, legg til linje 3 med linje 2 multiplisert med -24/51:

    La oss ekskludere elementene i den andre kolonnen i matrisen over hoveddiagonalen. For å gjøre dette, legg til linje 1 med linje 2 multiplisert med -3/17:

    Skill høyre side av matrisen. Den resulterende matrisen er den inverse matrisen til EN :

    Matriseform for å skrive et system med lineære ligninger: Ax=b, Hvor

    La oss beregne alle algebraiske komplementer til matrisen EN:

    ,
    ,
    ,
    ,
    ,

    Hvor EN ij − algebraisk komplement av et matriseelement EN, som ligger i krysset Jeg-te linje og j-th kolonne, og Δ er determinanten for matrisen EN.

    Ved å bruke den inverse matriseformelen får vi:

    I følge Cramers formler;

    Gauss-metoden;

    Løsning: Kronecker-Capelli teorem. Et system er konsistent hvis og bare hvis rangeringen til matrisen til dette systemet er lik rangeringen til den utvidede matrisen, dvs. r(EN)=r(A 1), Hvor

    Den utvidede matrisen til systemet ser slik ut:

    Multipliser den første linjen med ( –3 ), og den andre til ( 2 ); Etter dette, legg til elementene i den første linjen til de tilsvarende elementene i den andre linjen; trekk den tredje fra den andre linjen. I den resulterende matrisen lar vi den første raden være uendret.

    6 ) og bytt den andre og tredje linjen:

    Multipliser den andre linjen med ( –11 ) og legg til de tilsvarende elementene i den tredje linjen.

    Del elementene i den tredje linjen med ( 10 ).

    La oss finne determinanten til matrisen EN.

    Derfor, r(EN)=3 . Utvidet matriserangering r(A 1) er også lik 3 , dvs.

    r(EN)=r(A 1)=3 Þ Systemet er samarbeidende.

    1) Ved å undersøke systemet for konsistens, ble den utvidede matrisen transformert ved bruk av Gauss-metoden.

    Gaussmetoden er som følger:

    1. Redusere matrisen til en trekantet form, dvs. det skal være nuller under hoveddiagonalen (direkte bevegelse).

    2. Fra den siste ligningen finner vi x 3 og erstatte den med den andre, finner vi x 2, og vite x 3, x 2 vi erstatter dem i den første ligningen, finner vi x 1(omvendt).

    La oss skrive den gaussisk-transformerte utvidede matrisen

    i form av et system med tre ligninger:

    Þ x 3 = 1

    x 2 = x 3Þ x 3 = 1

    2x 1 =4+x 2 +x 3Þ 2x 1 =4+1+1Þ

    Þ 2x1 =6 Þ x 1 = 3

    .

    2) La oss løse systemet ved hjelp av Cramers formler: hvis determinanten til ligningssystemet Δ er forskjellig fra null, så har systemet en unik løsning, som finnes ved hjelp av formlene

    La oss beregne determinanten til systemet Δ:

    Fordi Hvis determinanten til systemet er forskjellig fra null, så har systemet ifølge Cramers regel en unik løsning. La oss beregne determinantene Δ 1 , Δ 2 , Δ 3 . De oppnås fra determinanten til systemet Δ ved å erstatte den tilsvarende kolonnen med en kolonne med frie koeffisienter.

    Vi finner de ukjente ved å bruke formlene:

    Svar: x 1 =3, x 2 =1, x 3 =1 .

    3) La oss løse systemet ved å bruke matriseregning, dvs. bruke den inverse matrisen.

    A×X=B Þ X=A -1 × B, Hvor A -1– invers matrise til EN,

    Kolonne med gratis medlemmer,

    Matrise-kolonne av ukjente.

    Den inverse matrisen beregnes ved å bruke formelen:

    Hvor D- matrisedeterminant EN, A ij– algebraiske komplementer til element a ij matriser EN. D= 60 (fra forrige avsnitt). Determinanten er ikke null, derfor er matrise A inverterbar, og dens inverse matrise kan finnes ved å bruke formel (*). La oss finne algebraiske komplementer for alle elementene i matrise A ved å bruke formelen:



    Og ij =(-1 )i+j M ij .

    x 1, x 2, x 3 gjorde hver ligning til en identitet, så ble de funnet riktig.

    Eksempel 6. Løs systemet ved hjelp av Gauss-metoden og finn to grunnleggende løsninger på systemet.



    Lignende artikler