Sådan finder du arealet af en rombe ved siden af. Fire formler, der kan bruges til at beregne arealet af en rombe

er et parallelogram, hvor alle sider er lige store, så gælder alle de samme formler for det som for et parallelogram, inklusive formlen for at finde arealet gennem produktet af højde og sider.

Arealet af en rombe kan findes ved også at kende dens diagonaler. Diagonalerne deler romben i fire helt ens retvinklede trekanter. Hvis vi sorterer dem for at få et rektangel, vil dets længde og bredde være lig med en hel diagonal og halvdelen af ​​den anden diagonal. Derfor findes arealet af en rhombus ved at gange diagonalerne af rhombus, reduceret med to (som arealet af det resulterende rektangel).

Hvis du kun har en vinkel og en side til din rådighed, så kan du bruge diagonalen som assistent og tegne den modsat den kendte vinkel. Derefter vil den opdele rhombus i to kongruente trekanter, hvis arealer vil lægge sammen for at give os arealet af rhombus. Arealet af hver trekant vil være lig med halvdelen af ​​produktet af kvadratet på siden og sinus af den kendte vinkel, som arealet af en ligebenet trekant. Da der er to sådanne trekanter, reduceres koefficienterne, hvilket kun efterlader siden til anden potens og sinus:

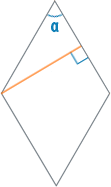
Hvis du indskriver en cirkel inde i en rombe, så vil dens radius forholde sig til siden i en vinkel på 90°, hvilket betyder, at to gange radius vil være lig med højden af ​​romben. Ved at erstatte højden h=2r i den foregående formel får vi areal S=ha=2ra

Hvis der sammen med radius af den indskrevne cirkel ikke er givet en side, men en vinkel, så skal du først finde siden ved at tegne højden på en sådan måde, at du får en retvinklet trekant med en given vinkel. Så kan side a findes ud fra trigonometriske relationer ved hjælp af formlen . Ved at erstatte dette udtryk med den samme standardformel for arealet af en rhombus, får vi

er et parallelogram, hvor alle sider er lige store.

En rhombus med rette vinkler kaldes en firkant og betragtes som et specialtilfælde af en rhombus. Du kan finde området af en rhombus på forskellige måder ved at bruge alle dens elementer - sider, diagonaler, højde. Den klassiske formel for arealet af en rombe er at beregne værdien gennem højden.

Et eksempel på beregning af arealet af en rhombus ved hjælp af denne formel er meget enkelt. Du skal blot erstatte dataene og beregne arealet.

Areal af en rombe gennem diagonaler

Diagonalerne på en rombe skærer hinanden i rette vinkler og er delt i to i skæringspunktet.

Formlen for arealet af en rombe gennem dens diagonaler er produktet af dens diagonaler divideret med 2.

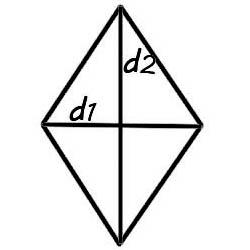Lad os se på et eksempel på beregning af arealet af en rhombus ved hjælp af diagonaler. Lad os få en rombe med diagonaler
d1 = 5 cm og d2 = 4. Lad os finde området.

Formlen for arealet af en rhombus gennem siderne indebærer også brugen af ​​andre elementer. Hvis en cirkel er indskrevet i en rombe, kan arealet af figuren beregnes ud fra siderne og dens radius:

Et eksempel på at beregne arealet af en rhombus gennem siderne er også meget enkelt. Du behøver kun at beregne radius af den indskrevne cirkel. Det kan udledes af Pythagoras sætning og ved hjælp af formlen.

Areal af en rombe gennem side og vinkel

Formlen for arealet af en rombe i form af side og vinkel bruges meget ofte.

Lad os se på et eksempel på at beregne arealet af en rhombus ved hjælp af en side og en vinkel.

Opgave: Givet en rombe, hvis diagonaler er d1 = 4 cm, d2 = 6 cm. Den spidse vinkel er α = 30°. Find arealet af figuren ved hjælp af siden og vinklen.
Lad os først finde siden af ​​romben. Vi bruger Pythagoras sætning til dette. Vi ved, at diagonalerne halverer sig i skæringspunktet og danner en ret vinkel. Derfor:
Lad os erstatte værdierne:
Nu kender vi siden og vinklen. Lad os finde området:

En rombe (fra det oldgræske ῥόμβος og fra det latinske rombus "tamburin") er et parallelogram, som er karakteriseret ved tilstedeværelsen af ​​sider af lige længde. Når vinklerne er 90 grader (eller en ret vinkel), kaldes en sådan geometrisk figur en firkant. En rombe er en geometrisk figur, en type firkant. Det kan både være et kvadrat og et parallelogram.

Oprindelsen af ​​dette udtryk

Lad os tale lidt om historien om denne figur, som vil hjælpe med at afsløre lidt de mystiske hemmeligheder i den antikke verden. Det velkendte ord for os, som ofte findes i skolelitteraturen, "rhombus", stammer fra det oldgræske ord "tamburin". I det antikke Grækenland blev disse musikinstrumenter produceret i en diamant- eller firkantet form (i modsætning til moderne enheder). Du har sikkert bemærket, at kortfarven - diamanter - har en rombisk form. Dannelsen af ​​denne kulør går tilbage til de tider, hvor runde diamanter ikke blev brugt i hverdagen. Derfor er rhombus den ældste historiske figur, der blev opfundet af menneskeheden længe før fremkomsten af ​​hjulet.

For første gang blev et ord som "rhombus" brugt af så berømte personligheder som Heron og paven af ​​Alexandria.

Egenskaber af en rombe

1. Da siderne af en rombe er modsat hinanden og parvis er parallelle, så er romben uden tvivl et parallelogram (AB || CD, AD || BC).
2. Rhombiske diagonaler skærer hinanden i rette vinkler (AC ⊥ BD), og er derfor vinkelrette. Derfor halverer skæringspunktet diagonalerne.
3. Rombevinklernes halveringslinjer er rombens diagonaler (∠DCA = ∠BCA, ∠ABD = ∠CBD osv.).
4. Af parallellogrammernes identitet følger det, at summen af ​​alle kvadraterne af diagonalerne på en rombe er tallet på kvadratet på siden, som multipliceres med 4.

Tegn på en diamant

En rombe er et parallelogram, når den opfylder følgende betingelser:

1. Alle sider af et parallelogram er lige store.
2. Diagonalerne på en rombe skærer en ret vinkel, det vil sige, at de er vinkelrette på hinanden (AC⊥BD). Dette beviser reglen om tre sider (siderne er lige store og i en vinkel på 90 grader).
3. Diagonalerne i et parallelogram deler vinklerne ligeligt, fordi siderne er lige store.

Område af en rombe

1. Arealet af en rombe er lig med det tal, der er halvdelen af ​​produktet af alle dens diagonaler.
2. Da en rhombus er en slags parallelogram, er arealet af rhombus (S) produktet af siden af ​​parallelogrammet og dets højde (h).
3. Derudover kan arealet af en rhombus beregnes ved hjælp af formlen, som er produktet af den kvadratiske side af rhombus og sinus af vinklen. Vinklens sinus er alfa - vinklen placeret mellem siderne af den oprindelige rombe.
4. En formel, der er produktet af to gange vinklen alfa og radius af den indskrevne cirkel (r), anses for ganske acceptabel for den korrekte løsning.

I artiklen vil vi overveje formel for rombeareal og ikke kun én! Vi viser dig på billederne, hvor nemt det er at være område af en rombe ved hjælp af simple formler.

Der er en lang række opgaver til at finde en eller anden mængde i en rombe, og de formler, der vil blive diskuteret, vil hjælpe os med dette.
En rhombus er en separat type firkant, fordi alle dens sider er lige store. Det repræsenterer også et specialtilfælde af et parallelogram, hvor siderne AB=BC=CD=AD er lige store.

Bemærk: Hvis du har brug for et kursus, test eller afhandling, så gå til webmath.ru. eller følg blot linket for at bestille kurser (http://www.webmath.ru/zakaz_kursovye.php).

En rombe har følgende egenskaber:

En rombe har lige store parallelle vinkler
- tilføjelsen af ​​to tilstødende vinkler er lig med 180 grader,
- Skæring af diagonaler i en vinkel på 90 grader,
- Halveringslinjen af ​​en rombe er dens diagonaler,
- Ved skæring er diagonalen opdelt i lige store dele.

En rombe har følgende egenskaber:

Hvis et parallelogram, hvor diagonalerne mødes i en vinkel på 90 grader, så kaldes det en rombe.
- Hvis et parallelogram, hvis halveringslinje er en diagonal, så kaldes det en rombe.
- Hvis et parallelogram har lige store sider, er det en rombe.
- Hvis en firkant har lige store sider, er det en rombe.
- Hvis en firkant, hvor halveringslinjen er en diagonal, og diagonalerne mødes i en vinkel på 90 grader, så er det en rombe.
- Hvis et parallelogram har samme højder, er det en rombe.

Fra ovenstående tegn kan vi konkludere, at de er nødvendige for at lære at adskille en rhombus fra andre figurer, der ligner den.

For i en rombe er alle sider ens omkredsen er efter følgende formel:
P=4a
Område med rombeformel

Der er flere formler. Den enkleste løses ved at tilføje arealet af 2 trekanter, som blev opnået ved at dividere diagonalerne.

Ved hjælp af den anden formel kan du løse problemer med kendte diagonaler på en rombe. I dette tilfælde vil arealet af rhombus være: summen af ​​diagonalerne divideret med to.

Det er meget nemt at løse og vil ikke blive glemt.

Den tredje formel kan bruges, når du kender vinklen mellem siderne. Når du kender det, kan du finde arealet af en rombe, det vil være lig med kvadratet af siderne gange vinklens sinus. Det gør ingen forskel hvilken vinkel. da sinus af en vinkel har samme værdi.

Det er vigtigt at huske, at arealet måles i kvadrater, og omkredsen måles i enheder. Disse formler er meget nemme at anvende i praksis.

Du kan også støde på problemer med at finde radius af en cirkel indskrevet i en rombe.

Der er også flere formler for dette:

Ved hjælp af den første formel findes radius som produktet af diagonalerne divideret med tallet opnået ved at tilføje alle sider. eller lig med halvdelen af ​​højden (r=h/2).

Den anden formel tager princippet fra den første og gælder, at vi kender diagonalerne og siderne af en rombe.

I den tredje formel kommer radius fra højden af ​​den mindre trekant, der kommer fra skæringspunktet.

Definition af en diamant

Rhombus er et parallelogram, hvor alle sider er lig med hinanden.

Online lommeregner

Hvis siderne af en rombe danner en ret vinkel, så får vi firkant.

Diagonalerne på en rombe skærer hinanden i rette vinkler.
Diagonalerne på en rombe er halveringslinjen af ​​dens vinkler.

Arealet af en rhombus, ligesom områderne med de fleste geometriske former, kan findes på flere måder. Lad os forstå deres essens og overveje eksempler på løsninger.

Formel for arealet af en rombe ved side og højde

Lad os få en rhombus med en side a a -en og højde h h h, trukket til denne side. Da en rhombus er et parallelogram, finder vi dens areal på samme måde som arealet af et parallelogram.

S = a ⋅ h S=a\cdot h S=en ⋅h

A a -en- side;
h h h- højde sænket til siden a a -en.

Lad os løse et simpelt eksempel.

Eksempel

Siden af ​​en rombe er 5 (cm). Højden sænket til denne side har en længde på 2 (cm). Find arealet af en rombe S S S.

Løsning

A = 5 a = 5 a =5
h = 2 h = 2 h =2

Vi bruger vores formel og beregner:
S = a ⋅ h = 5 ⋅ 2 = 10 S=a\cdot h=5\cdot 2=10S=en ⋅h =5 ⋅ 2 = 1 0 (se sq.)

Svar: 10 cm kvm.

Formel for arealet af en rombe ved hjælp af diagonaler

Alt er lige så enkelt her. Du skal bare tage halvdelen af ​​produktet af diagonalerne og få området.

S = 1 2 ⋅ d 1 ⋅ d 2 S=\frac(1)(2)\cdot d_1\cdot d_2S=2 1 ​ ⋅ d 1 ​ ⋅ d 2 ​

D 1, d 2 d_1, d_2 d 1 ​ , d 2 ​ - diagonaler af en rombe.

Eksempel

En af diagonalerne på en rombe er 7 (cm), og den anden er 2 gange større end den første. Find arealet af figuren.

Løsning

D1 = 7 d_1=7 d 1 ​ = 7
d 2 = 2 ⋅ d 1 d_2=2\cdot d_1d 2 ​ = 2 ⋅ d 1 ​

Lad os finde den anden diagonal:
d 2 = 2 ⋅ d 1 = 2 ⋅ 7 = 14 d_2=2\cdot d_1=2\cdot 7=14d 2 ​ = 2 ⋅ d 1 ​ = 2 ⋅ 7 = 1 4
Så området:
S = 1 2 ⋅ 7 ⋅ 14 = 49 S=\frac(1)(2)\cdot7\cdot14=49S=2 1 ​ ⋅ 7 ⋅ 1 4 = 4 9 (se sq.)

Svar: 49 cm kvm.

Formel for arealet af en rombe ved hjælp af to sider og vinklen mellem dem

S = a 2 ⋅ sin ⁡ (α) S=a^2\cdot\sin(\alpha)S=-en 2 ⋅ synd(α)

A a -en- side af rhombus;
α\alfa α - enhver vinkel på romben.

Eksempel

Find arealet af en rombe, hvis hver af dens sider er 10 cm og vinklen mellem to tilstødende sider er 30 grader.

Løsning

A = 10 a = 10 a =1 0
α = 3 0 ∘ \alpha=30^(\circ)α = 3 0 ∘

Ved hjælp af formlen får vi:
S = a 2 ⋅ sin ⁡ (α) = 100 ⋅ sin ⁡ (3 0 ∘) = 50 S=a^2\cdot\sin(\alpha)=100\cdot\sin(30^(\circ))= 50S=-en 2 ⋅ sin(α) =1 0 0 ⋅ synd (3 0 ∘ ) = 5 0 (se sq.)

Svar: 50 cm kvm.

Formel for arealet af en rombe baseret på radius af den indskrevne cirkel og vinkel

S = 4 ⋅ r 2 sin ⁡ (α) S=\frac(4\cdot r^2)(\sin(\alpha))S=synd(α)4 ⋅ r 2 ​

R r r- radius af den indskrevne cirkel i en rombe;
α\alfa α - enhver vinkel på romben.

Eksempel

Find arealet af en rombe, hvis vinklen mellem baserne er 60 grader og radius af den indskrevne cirkel er 4 (cm).

Løsning

R = 4 r = 4 r =4
α = 6 0 ∘ \alpha=60^(\circ)α = 6 0 ∘

S = 4 ⋅ r 2 sin ⁡ (α) = 4 ⋅ 16 sin ⁡ (6 0 ∘) ≈ 73,9 S=\frac(4\cdot r^2)(\sin(\alpha))=\frac(4\ cdot 16)(\sin(60^(\circ)))\approx73.9S=synd(α)4 ⋅ r 2 ​ = synd (6 0 ∘ ) 4 ⋅ 1 6 ​ ≈ 7 3 . 9 (se sq.)

Svar: 73,9 cm kvm.

Formel for arealet af en rhombus baseret på radius af den indskrevne cirkel og side

S = 2 ⋅ a ⋅ r S=2\cdot a\cdot rS=2 ⋅ en ⋅r

A a -en-side af romben;
r r r- radius af den indskrevne cirkel i en rombe.

Eksempel

Lad os tage betingelsen fra den forrige opgave, men lad os i stedet for vinklen kende siden af ​​rhombus lig med 5 cm.

Løsning

A = 5 a = 5 a =5
r = 4 r = 4 r =4

S = 2 ⋅ a ⋅ r = 2 ⋅ 5 ⋅ 4 = 40 S=2\cdot a\cdot r=2\cdot5\cdot4=40S=2 ⋅ en ⋅r =2 ⋅ 5 ⋅ 4 = 4 0 (se sq.)

Svar: 40 cm kvm.