Løs lineær matrixligning. omvendt matrix
Lad os få et system af lineære ligninger med 
ukendt:
Vi vil antage, at hovedmatrixen 
ikke-degenereret. Så ved sætning 3.1 eksisterer der en invers matrix 
Multiplicering af matrixligningen 
til matrixen 
til venstre, ved hjælp af definition 3.2, samt udsagn 8) af sætning 1.1, får vi formlen, som matrixmetoden til løsning af lineære ligningssystemer er baseret på:
Kommentar. Bemærk, at matrixmetoden til løsning af lineære ligningssystemer i modsætning til Gauss-metoden har begrænset anvendelse: denne metode kan kun løse lineære ligningssystemer, for hvilke for det første antallet af ubekendte er lig med antallet af ligninger, og for det andet er hovedmatrixen ikke-singular.
Eksempel. Løs et system af lineære ligninger ved hjælp af matrixmetoden.
Et system af tre lineære ligninger med tre ukendte er givet 
Hvor
Hovedmatrixen i ligningssystemet er ikke-singular, da dens determinant er ikke-nul:
Invers matrix 
Lad os komponere ved hjælp af en af metoderne beskrevet i afsnit 3.
Ved at bruge formlen for matrixmetoden til løsning af lineære ligningssystemer får vi
5.3. Cramer metode
Denne metode, ligesom matrixmetoden, er kun anvendelig for systemer af lineære ligninger, hvor antallet af ukendte falder sammen med antallet af ligninger. Cramers metode er baseret på sætningen af samme navn:
Sætning 5.2.
System 
lineære ligninger med 
ukendt
hvis hovedmatrix er ikke-singular, har en unik løsning, der kan opnås ved hjælp af formlerne
Hvor 
determinant for en matrix afledt af basismatrixen 
ligningssystem ved at erstatte det 
kolonne med en kolonne af frie medlemmer.
Eksempel.
Lad os finde løsningen på systemet af lineære ligninger, der blev betragtet i det foregående eksempel, ved hjælp af Cramers metode. Ligningssystemets hovedmatrix er ikke-degenereret, da 
Lad os beregne determinanterne 
Ved hjælp af formlerne præsenteret i sætning 5.2 beregner vi værdierne af de ukendte:
6. Undersøgelse af lineære ligningssystemer.
Grundlæggende løsning
At studere et system af lineære ligninger betyder at bestemme, om dette system er kompatibelt eller inkompatibelt, og hvis det er kompatibelt, at finde ud af, om dette system er bestemt eller ubestemt.
Kompatibilitetsbetingelsen for et system af lineære ligninger er givet af følgende sætning
Sætning 6.1 (Kronecker–Capelli).
Et system af lineære ligninger er konsistent, hvis og kun hvis rangeringen af systemets hovedmatrix er lig med rangordenen af dets udvidede matrix:
For et simultant system af lineære ligninger løses spørgsmålet om dets bestemthed eller usikkerhed ved hjælp af følgende teoremer.
Sætning 6.2. Hvis rangeringen af hovedmatrixen i et fælles system er lig med antallet af ukendte, så er systemet bestemt
Sætning 6.3. Hvis rangeringen af hovedmatrixen i et fælles system er mindre end antallet af ukendte, så er systemet usikkert.
Fra de formulerede teoremer følger således en metode til at studere systemer af lineære algebraiske ligninger. Lade n- antal ukendte, 
Derefter:
Definition 6.1. Den grundlæggende løsning af et ubestemt system af lineære ligninger er en løsning, hvor alle frie ubekendte er lig med nul.
Eksempel. Udforsk et system af lineære ligninger. Hvis systemet er usikkert, så find dets grundlæggende løsning.
Lad os beregne rækkerne af de vigtigste 
og udvidede matricer 
af dette ligningssystem, for hvilket vi bringer systemets udvidede (og samtidig hovedmatrixen) til en trinvis form:
Tilføj den anden række af matricen til dens første række ganget med 
tredje linje - med den første linje ganget med 
og den fjerde linje - med den første, ganget med 
vi får en matrix
Til den tredje række i denne matrix lægger vi den anden række ganget med 
og til den fjerde linje – den første, ganget med 
Som et resultat får vi matrixen
fjernelse af den tredje og fjerde række, hvorfra vi får en trinmatrix
Dermed, 
Følgelig er dette system af lineære ligninger konsistent, og da rangværdien er mindre end antallet af ukendte, er systemet usikkert. Trinmatrixen opnået som et resultat af elementære transformationer svarer til ligningssystemet
Ukendt 
Og 
er de vigtigste, og de ukendte 
Og 
gratis. Ved at tildele nulværdier til de frie ubekendte får vi en grundlæggende løsning på dette lineære ligningssystem.
Et system af m lineære ligninger med n ukendte kaldet et formsystem
Hvor en ij Og b i (jeg=1,…,m; b=1,…,n) er nogle kendte tal, og x 1,...,x n- ukendt. I udpegningen af koefficienter en ij første indeks jeg angiver ligningstallet, og det andet j– antallet af den ukendte, som denne koefficient står på.
Vi vil skrive koefficienterne for de ukendte i form af en matrix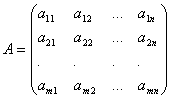 
, som vi kalder matrix af systemet.
Tallene på højre side af ligningerne er b 1,…,b m hedder gratis medlemmer.
Totalitet n tal c 1,...,c n hedder afgørelse af et givet system, hvis hver ligning i systemet bliver en lighed efter at have erstattet tal i det c 1,...,c n i stedet for de tilsvarende ukendte x 1,...,x n.
Vores opgave bliver at finde løsninger på systemet. I dette tilfælde kan der opstå tre situationer:
Et system af lineære ligninger, der har mindst én løsning kaldes samling. Ellers, dvs. hvis systemet ikke har nogen løsninger, så kaldes det ikke-fælles.
Lad os overveje måder at finde løsninger på systemet på.
MATRIXMETODE TIL LØSNING AF SYSTEMER AF LINEÆRE LIGNINGER
Matricer gør det muligt kort at nedskrive et system af lineære ligninger. Lad et system af 3 ligninger med tre ukendte være givet:
Overvej systemmatricen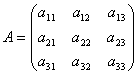 
og matrixkolonner med ukendte og frie udtryk 
Lad os finde arbejdet
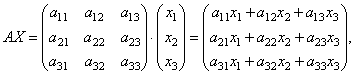
de der. som et resultat af produktet får vi venstre side af ligningerne i dette system. Derefter, ved hjælp af definitionen af matrix-lighed, kan dette system skrives i formen
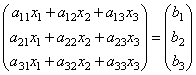eller kortere EN∙X=B.
Her er matricerne EN Og B er kendt, og matrixen x ukendt. Det er nødvendigt at finde det, fordi... dets elementer er løsningen på dette system. Denne ligning kaldes matrix ligning.
Lad determinanten af matricen være forskellig fra nul | EN| ≠ 0. Så løses matrixligningen som følger. Multiplicer begge sider af ligningen til venstre med matrixen A-1, omvendt af matrixen EN: . Fordi A -1 A = E Og E∙X = X, så får vi en løsning til matrixligningen på formen X = A -1 B .
Bemærk, at da den inverse matrix kun kan findes for kvadratiske matricer, kan matrixmetoden kun løse de systemer, hvor antallet af ligninger falder sammen med antallet af ukendte. Matrixregistrering af systemet er dog også mulig i det tilfælde, hvor antallet af ligninger ikke er lig med antallet af ukendte, så er matrixen EN vil ikke være firkantet og derfor er det umuligt at finde en løsning på systemet i skemaet X = A -1 B.
Eksempler. Løs ligningssystemer.
CRAMERS REGEL
Overvej et system af 3 lineære ligninger med tre ukendte:
Tredjeordens determinant svarende til systemmatricen, dvs. sammensat af koefficienter for ukendte,
hedder determinant for systemet.
Lad os sammensætte yderligere tre determinanter som følger: Erstat sekventielt 1, 2 og 3 kolonner i determinanten D med en kolonne med frie led
Så kan vi bevise følgende resultat.
Sætning (Cramers regel). Hvis determinanten for systemet Δ ≠ 0, så har det pågældende system én og kun én løsning, og
Bevis. Så lad os overveje et system med 3 ligninger med tre ubekendte. Lad os gange systemets 1. ligning med det algebraiske komplement A 11 element en 11, 2. ligning – på A 21 og 3. – på A 31:
Lad os tilføje disse ligninger:
Lad os se på hver af parenteserne og højre side af denne ligning. Ved sætningen om udvidelsen af determinanten i elementer i 1. kolonne
På samme måde kan det vises, at og .
Endelig er det let at bemærke det 
Dermed opnår vi ligheden: .
Derfor,.
Lighederne og er afledt på samme måde, hvoraf sætningens udsagn følger.
Således bemærker vi, at hvis determinanten af systemet Δ ≠ 0, så har systemet en unik løsning og omvendt. Hvis systemets determinant er lig med nul, så har systemet enten et uendeligt antal løsninger eller har ingen løsninger, dvs. uforenelig.
Eksempler. Løs ligningssystem
GAUSS METODE
De tidligere omtalte metoder kan kun bruges til at løse de systemer, hvor antallet af ligninger falder sammen med antallet af ukendte, og systemets determinant skal være forskellig fra nul. Gauss-metoden er mere universel og velegnet til systemer med et vilkårligt antal ligninger. Det består i den konsekvente eliminering af ubekendte fra systemets ligninger.
Overvej igen et system af tre ligninger med tre ukendte:
.
Vi vil lade den første ligning være uændret, og fra den 2. og 3. vil vi udelukke de termer, der indeholder x 1. For at gøre dette skal du dividere den anden ligning med EN 21 og gange med – EN 11, og føj det derefter til den 1. ligning. På samme måde dividerer vi den tredje ligning med EN 31 og gange med – EN 11, og tilføj det derefter med den første. Som et resultat vil det originale system have formen:
Nu fra den sidste ligning eliminerer vi udtrykket indeholdende x 2. For at gøre dette skal du dividere den tredje ligning med, gange med og addere med den anden. Så får vi et ligningssystem:
Herfra er det let at finde fra den sidste ligning x 3, derefter fra 2. ligning x 2 og endelig fra 1. x 1.
Ved brug af Gauss-metoden kan ligningerne byttes om, hvis det er nødvendigt.
I stedet for at skrive et nyt ligningssystem begrænser de sig ofte til at skrive systemets udvidede matrix:
og derefter bringe det til en trekantet eller diagonal form ved hjælp af elementære transformationer.
TIL elementære transformationer matricer inkluderer følgende transformationer:
- omarrangering af rækker eller kolonner;
- at gange en streng med et andet tal end nul;
- tilføjelse af andre linjer til en linje.
Eksempler: Løs ligningssystemer ved hjælp af Gauss-metoden.
Systemet har således et uendeligt antal løsninger.
Løsning af systemer af lineære algebraiske ligninger ved hjælp af matrixmetoden (ved hjælp af en invers matrix).
Lad systemet af lineære algebraiske ligninger være givet i matrixform , hvor matrixen EN har dimension n på n og dens determinant er ikke-nul.
Siden , så matrixen EN– er invertibel, det vil sige, at der er en invers matrix. Hvis vi multiplicerer begge sider af ligheden til venstre, får vi en formel til at finde en matrix-søjle af ukendte variable. Sådan fik vi en løsning til et system af lineære algebraiske ligninger ved hjælp af matrixmetoden.
matrix metode.
Lad os omskrive ligningssystemet i matrixform: 
Fordi 
så kan SLAE løses ved hjælp af matrixmetoden. Ved hjælp af den inverse matrix kan løsningen til dette system findes som 
.
Lad os konstruere en invers matrix ved hjælp af en matrix ud fra algebraiske komplementer af matrixelementer EN(se om nødvendigt artiklens metoder for at finde den inverse matrix): 
Det er tilbage at beregne matrixen af ukendte variable ved at gange den inverse matrix 
til en matrix-kolonne af gratis medlemmer (se om nødvendigt artiklens operationer om matricer): 
eller i et andet indlæg x 1
= 4, x 2
= 0, x 3
= -1
.
Hovedproblemet, når man finder løsninger på systemer af lineære algebraiske ligninger ved hjælp af matrixmetoden, er kompleksiteten i at finde den inverse matrix, især for kvadratiske matricer af større orden end tredje.
For en mere detaljeret beskrivelse af teorien og yderligere eksempler, se artikelmatrixmetoden til løsning af lineære ligningssystemer.
Øverst på siden
Løsning af lineære ligningssystemer ved hjælp af Gauss-metoden.
Antag at vi skal finde en løsning på systemet fra n lineære ligninger med n ukendte variable 
hvis determinant af hovedmatrixen er forskellig fra nul.
Essensen af Gauss-metoden består af sekventiel eliminering af ukendte variable: først eliminering x 1 fra alle systemets ligninger, startende fra den anden, er yderligere udelukket x 2 fra alle ligninger, startende med den tredje, og så videre, indtil kun den ukendte variabel er tilbage i den sidste ligning x n. Denne proces med at transformere systemligninger for sekventielt at eliminere ukendte variable kaldes direkte gaussisk metode. Efter at have afsluttet den fremadgående progression af den Gaussiske metode, fra den sidste ligning finder vi x n, ved at bruge denne værdi fra den næstsidste ligning, vi beregner x n-1, og så videre, fra den første ligning, vi finder x 1 . Processen med at beregne ukendte variable, når man går fra den sidste ligning i systemet til den første, kaldes omvendt af Gauss-metoden.
Lad os kort beskrive algoritmen til at eliminere ukendte variable.
Det vil vi antage, da vi altid kan opnå dette ved at udveksle systemets ligninger. Fjern den ukendte variabel x 1
fra alle systemets ligninger, startende fra den anden. For at gøre dette, til den anden ligning i systemet lægger vi den første, ganget med, til den tredje ligning lægger vi den første, ganget med, og så videre, til nth til ligningen lægger vi den første ganget med. Ligningssystemet efter sådanne transformationer vil antage formen 
hvor og 
.
Vi ville nå frem til det samme resultat, hvis vi udtrykte det x 1 gennem andre ukendte variable i systemets første ligning, og det resulterende udtryk blev substitueret i alle andre ligninger. Altså variablen x 1 udelukket fra alle ligninger, startende fra den anden.
Dernæst fortsætter vi på lignende måde, men kun med en del af det resulterende system, som er markeret i figuren 
For at gøre dette lægger vi til den tredje ligning i systemet den anden, ganget med, til den fjerde ligning lægger vi den anden, ganget med, og så videre, til nth til ligningen lægger vi sekundet ganget med. Ligningssystemet efter sådanne transformationer vil antage formen 
hvor og 
. Altså variablen x 2
udelukket fra alle ligninger fra den tredje.
Dernæst fortsætter vi med at eliminere det ukendte x 3
, i dette tilfælde handler vi på samme måde med den del af systemet, der er markeret på figuren 
Så vi fortsætter den direkte progression af den Gaussiske metode, indtil systemet tager formen 
Fra dette øjeblik begynder vi det omvendte af Gauss-metoden: vi beregner x n fra den sidste ligning som ved hjælp af den opnåede værdi x n vi finder x n-1 fra næstsidste ligning, og så videre, finder vi x 1 fra den første ligning.
Løs system af lineære ligninger 
Gauss metode.
Fjern den ukendte variabel x 1
fra systemets anden og tredje ligning. For at gøre dette tilføjer vi til begge sider af den anden og tredje ligning de tilsvarende dele af den første ligning, ganget med henholdsvis og: 
Lad os nu udelukke fra den tredje ligning x 2
, ved at lægge venstre og højre side af den anden ligning til dens venstre og højre side ganget med: 
Dette fuldender det fremadgående slag af Gauss-metoden, vi begynder det omvendte slag.
Fra den sidste ligning af det resulterende ligningssystem finder vi x 3
:
Fra den anden ligning får vi .
Fra den første ligning finder vi den resterende ukendte variabel og afslutter derved det omvendte af Gauss-metoden.
x 1 = 4, x 2 = 0, x 3 = -1 .
For mere detaljeret information og yderligere eksempler, se afsnittet om løsning af elementære systemer af lineære algebraiske ligninger ved hjælp af Gauss-metoden.
Øverst på siden
Denne online lommeregner løser et system af lineære ligninger ved hjælp af matrixmetoden. Der gives en meget detaljeret løsning. For at løse et system af lineære ligninger skal du vælge antallet af variable. Vælg en metode til at beregne den inverse matrix. Indtast derefter dataene i cellerne og klik på knappen "Beregn".
×
Advarsel
Vil du rydde alle celler?
Luk Ryd
Instruktioner til indtastning af data. Tal indtastes som heltal (eksempler: 487, 5, -7623 osv.), decimaler (eks. 67., 102.54 osv.) eller brøker. Brøken skal indtastes på formen a/b, hvor a og b er heltal eller decimaler. Eksempler 45/5, 6,6/76,4, -7/6,7 osv.
Matrixmetode til løsning af lineære ligningssystemer
Overvej følgende system af lineære ligninger:
Givet definitionen af en invers matrix, har vi EN −1 EN=E, Hvor E- identitetsmatrix. Derfor kan (4) skrives som følger:
For at løse systemet af lineære ligninger (1) (eller (2)), er det således nok at gange det inverse af EN matrix pr. begrænsningsvektor b.
Eksempler på løsning af et system af lineære ligninger ved hjælp af matrixmetoden
Eksempel 1. Løs følgende system af lineære ligninger ved hjælp af matrixmetoden:
Lad os finde det omvendte af matrix A ved hjælp af Jordan-Gauss-metoden. På højre side af matrixen EN Lad os skrive identitetsmatrixen:
Lad os udelukke elementerne i den 1. kolonne i matricen under hoveddiagonalen. For at gøre dette skal du tilføje linje 2,3 med linje 1, ganget med henholdsvis -1/3, -1/3:
Lad os udelukke elementerne i 2. kolonne i matrixen under hoveddiagonalen. For at gøre dette skal du tilføje linje 3 med linje 2 ganget med -24/51:
Lad os udelukke elementerne i 2. kolonne i matricen over hoveddiagonalen. For at gøre dette skal du tilføje linje 1 med linje 2 ganget med -3/17:
Adskil højre side af matrixen. Den resulterende matrix er den inverse matrix af EN :
Matrixform til at skrive et system af lineære ligninger: Ax=b, Hvor
Lad os beregne alle algebraiske komplementer af matricen EN:
 ,
|
 ,
|
 ,
|
 ,
|
 ,
|
Hvor EN ij − algebraisk komplement af et matrixelement EN, beliggende i krydset jeg-th linje og j-th kolonne, og Δ er determinanten for matrixen EN.
Ved at bruge den inverse matrixformel får vi:
Ifølge Cramers formler;
Gauss metode;
Løsning: Kronecker-Capelli-sætning. Et system er konsistent, hvis og kun hvis rangordenen af dette systems matrix er lig med rangordenen for dets udvidede matrix, dvs. r(EN)=r(A 1), Hvor
Systemets udvidede matrix ser sådan ud:
Gang den første linje med ( –3 ), og den anden til ( 2 ); Herefter skal du tilføje elementerne i den første linje til de tilsvarende elementer i den anden linje; trække den tredje fra den anden linje. I den resulterende matrix forlader vi den første række uændret.
6 ) og skift anden og tredje linje:
Gang den anden linje med ( –11 ) og føj til de tilsvarende elementer i den tredje linje.
Divider elementerne i den tredje linje med ( 10 ).
Lad os finde determinanten for matricen EN.
Derfor, r(EN)=3 . Udvidet Matrix Rank r(A 1) er også lige 3 , dvs.
r(EN)=r(A 1)=3 Þ Systemet er samarbejdende.
1) Ved undersøgelse af systemet for konsistens blev den udvidede matrix transformeret ved hjælp af Gauss-metoden.
Den Gaussiske metode er som følger:
1. Reduktion af matricen til en trekantet form, dvs. der skal være nuller under hoveddiagonalen (direkte bevægelse).
2. Fra den sidste ligning finder vi x 3 og erstatte det med det andet, finder vi x 2, og at vide x 3, x 2 vi erstatter dem i den første ligning, finder vi x 1(baglæns).
Lad os skrive den Gauss-transformerede udvidede matrix
i form af et system af tre ligninger:
Þ x 3 = 1
x 2 = x 3Þ x 3 = 1
2x 1 =4+x 2 +x 3Þ 2x1 =4+1+1Þ
Þ 2x1 =6 Þ x 1 = 3
.
2) Lad os løse systemet ved hjælp af Cramers formler: hvis determinanten af ligningssystemet Δ er forskellig fra nul, så har systemet en unik løsning, som findes ved hjælp af formlerne
Lad os beregne determinanten for systemet Δ:
Fordi Hvis systemets determinant er forskellig fra nul, så har systemet ifølge Cramers regel en unik løsning. Lad os beregne determinanterne Δ 1 , Δ 2 , Δ 3 . De opnås fra determinanten af systemet Δ ved at erstatte den tilsvarende kolonne med en kolonne med frie koefficienter.
Vi finder de ukendte ved hjælp af formlerne:
Svar: x 1 =3, x 2 =1, x 3 =1 .
3) Lad os løse systemet ved hjælp af matrixregning, altså ved hjælp af den inverse matrix.
A×X=B Þ X=A -1 × B, Hvor A -1– omvendt matrix til EN,
Kolonne af gratis medlemmer,
Matrix-kolonne af ukendte.
Den inverse matrix beregnes ved hjælp af formlen:
Hvor D- matrixdeterminant EN, A ij– algebraiske komplementer til element a ij matricer EN. D= 60 (fra forrige afsnit). Determinanten er ikke-nul, derfor er matrix A inverterbar, og dens inverse matrix kan findes ved hjælp af formel (*). Lad os finde algebraiske komplementer til alle elementer i matrix A ved hjælp af formlen:
Og ij =(-1 )i+j M ij .
x 1, x 2, x 3 gjorde hver ligning til en identitet, så blev de fundet korrekt.
Eksempel 6. Løs systemet ved hjælp af Gauss-metoden og find to vilkårlige grundlæggende løsninger til systemet.
Lignende artikler
De bedste amuletter mod det onde øje og skader Amulet mod det onde øje med hænder til børn
Sådan læser du Salteren korrekt
Lækre retter med pølser
Et glimt af Bella. Romantisk kronik. Et glimt af genialitet. Messerer om Akhmadulina Boris Messerer glimt af Bella romantiske krønike
Jeg drømte, at jeg sejlede på en båd på floden
Sådan tilberedes okse-entrecote i en stegepande
Om virksomheden Kurser i fremmedsprog ved Moscow State University
Hvilken by og hvorfor blev den vigtigste i det gamle Mesopotamien?
Hvorfor Bukhsoft Online er bedre end et almindeligt regnskabsprogram!
Hvilket år er et skudår, og hvordan beregnes det