Hvordan finne området til en rombe ved side. Fire formler som kan brukes til å beregne arealet til en rombe

er et parallellogram der alle sider er like, så gjelder alle de samme formlene for det som for et parallellogram, inkludert formelen for å finne arealet gjennom produktet av høyde og sider.

Området til en rombe kan bli funnet ved også å kjenne diagonalene. Diagonalene deler romben i fire helt like rette trekanter. Hvis vi sorterer dem for å få et rektangel, vil lengden og bredden være lik en hel diagonal og halvparten av den andre diagonalen. Derfor blir arealet til en rombe funnet ved å multiplisere diagonalene til romben, redusert med to (som arealet av det resulterende rektangelet).

Hvis du bare har en vinkel og en side til rådighet, så kan du bruke diagonalen som en assistent og tegne den motsatt av den kjente vinkelen. Deretter vil den dele romben i to kongruente trekanter, hvis arealer vil legge sammen for å gi oss arealet til romben. Arealet til hver av trekantene vil være lik halvparten av produktet av kvadratet på siden og sinusen til den kjente vinkelen, som arealet av en likebenet trekant. Siden det er to slike trekanter, reduseres koeffisientene, og etterlater bare siden til andre potens og sinus:

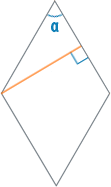
Hvis du skriver inn en sirkel inne i en rombe, vil dens radius forholde seg til siden i en vinkel på 90°, noe som betyr at to ganger radius vil være lik høyden på romben. Ved å erstatte i stedet for høyden h=2r i forrige formel, får vi arealet S=ha=2ra

Hvis det sammen med radiusen til den innskrevne sirkelen ikke er gitt en side, men en vinkel, må du først finne siden ved å tegne høyden på en slik måte at du får en rettvinklet trekant med en gitt vinkel. Da kan side a bli funnet fra trigonometriske relasjoner ved å bruke formelen . Ved å erstatte dette uttrykket med den samme standardformelen for arealet til en rombe, får vi

er et parallellogram der alle sider er like.

En rombe med rette vinkler kalles en firkant og regnes som et spesialtilfelle av en rombe. Du kan finne området til en rombe på forskjellige måter, ved å bruke alle dens elementer - sider, diagonaler, høyde. Den klassiske formelen for arealet til en rombe er å beregne verdien gjennom høyden.

Et eksempel på å beregne arealet til en rombe ved hjelp av denne formelen er veldig enkelt. Du trenger bare å erstatte dataene og beregne arealet.

Området til en rombe gjennom diagonaler

Diagonalene til en rombe skjærer hverandre i rette vinkler og er delt i to i skjæringspunktet.

Formelen for arealet til en rombe når det gjelder diagonalene er produktet av diagonalene delt på 2.

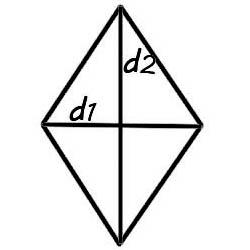La oss se på et eksempel på beregning av arealet til en rombe ved hjelp av diagonaler. La oss få en rombe med diagonaler
d1 = 5 cm og d2 = 4. La oss finne området.

Formelen for arealet til en rombe gjennom sidene innebærer også bruk av andre elementer. Hvis en sirkel er innskrevet i en rombe, kan arealet av figuren beregnes fra sidene og dens radius:

Et eksempel på å beregne arealet til en rombe gjennom sidene er også veldig enkelt. Du trenger bare å beregne radiusen til den innskrevne sirkelen. Det kan avledes fra Pythagoras teorem og ved å bruke formelen.

Arealet av en rombe gjennom side og vinkel

Formelen for arealet til en rombe når det gjelder side og vinkel brukes veldig ofte.

La oss se på et eksempel på å beregne arealet til en rombe ved å bruke en side og en vinkel.

Oppgave: Gitt en rombe hvis diagonaler er d1 = 4 cm, d2 = 6 cm. Den spisse vinkelen er α = 30°. Finn arealet av figuren ved å bruke siden og vinkelen.
La oss først finne siden av romben. Vi bruker Pythagoras teorem til dette. Vi vet at i skjæringspunktet halverer diagonalene og danner en rett vinkel. Derfor:
La oss erstatte verdiene:
Nå vet vi siden og vinkelen. La oss finne området:

En rombe (fra det antikke greske ῥόμβος og fra det latinske rombus "tamburin") er et parallellogram, som er preget av tilstedeværelsen av sider med like lange. Når vinklene er 90 grader (eller rett vinkel), kalles en slik geometrisk figur en firkant. En rombe er en geometrisk figur, en type firkant. Det kan være både et kvadrat og et parallellogram.

Opprinnelsen til dette begrepet

La oss snakke litt om historien til denne figuren, som vil hjelpe oss med å avdekke litt av de mystiske hemmelighetene til den antikke verden. Det kjente ordet for oss, som ofte finnes i skolelitteraturen, "rhombus", stammer fra det gamle greske ordet "tamburin". I antikkens Hellas ble disse musikkinstrumentene produsert i en diamant eller firkantet form (i motsetning til moderne enheter). Du la sikkert merke til at kortfargen - diamanter - har en rombisk form. Dannelsen av denne drakten går tilbake til tiden da runde diamanter ikke ble brukt i hverdagen. Følgelig er romben den eldste historiske figuren som ble oppfunnet av menneskeheten lenge før fremkomsten av hjulet.

For første gang ble et slikt ord som "rhombus" brukt av så kjente personligheter som Heron og paven av Alexandria.

Egenskaper til en rombe

1. Siden sidene til en rombe er motsatte hverandre og er parallelle i par, så er romben utvilsomt et parallellogram (AB || CD, AD || BC).
2. Rombediagonaler skjærer hverandre i rette vinkler (AC ⊥ BD), og er derfor vinkelrett. Derfor halverer skjæringspunktet diagonalene.
3. Halveringslinjene til rombiske vinkler er diagonalene til romben (∠DCA = ∠BCA, ∠ABD = ∠CBD, etc.).
4. Fra identiteten til parallellogrammer følger det at summen av alle kvadratene til diagonalene til en rombe er tallet på kvadratet på siden, som multipliseres med 4.

Tegn på en diamant

En rombe er et parallellogram når den oppfyller følgende betingelser:

1. Alle sider av et parallellogram er like.
2. Diagonalene til en rombe skjærer en rett vinkel, det vil si at de er vinkelrette på hverandre (AC⊥BD). Dette beviser regelen om tre sider (sidene er like og i en vinkel på 90 grader).
3. Diagonalene til et parallellogram deler vinklene likt fordi sidene er like.

Området til en rombe

1. Arealet til en rombe er lik tallet som er halvparten av produktet av alle diagonalene.
2. Siden en rombe er et slags parallellogram, er arealet av romben (S) produktet av siden av parallellogrammet og dens høyde (h).
3. I tillegg kan arealet til en rombe beregnes ved hjelp av formelen, som er produktet av den kvadratiske siden av romben og sinusen til vinkelen. Vinkelens sinus er alfa - vinkelen som ligger mellom sidene til den opprinnelige romben.
4. En formel som er produktet av to ganger vinkelen alfa og radiusen til den innskrevne sirkelen (r) anses som ganske akseptabel for riktig løsning.

I artikkelen vil vi vurdere formel for rombeareal og ikke bare en! Vi viser deg på bildene hvor enkelt det er å være område av en rombe ved hjelp av enkle formler.

Det er et stort antall oppgaver for å finne en eller annen mengde i en rombe, og formlene som vil bli diskutert vil hjelpe oss med dette.
En rombe er en egen type firkant fordi alle sidene er like. Det representerer også et spesialtilfelle av et parallellogram der sidene AB=BC=CD=AD er like.

Merk: Hvis du trenger et kurs, test eller avhandling, gå til webmath.ru. eller bare følg lenken for å bestille kurs (http://www.webmath.ru/zakaz_kursovye.php).

En rombe har følgende egenskaper:

En rombe har like parallelle vinkler
- tillegg av to tilstøtende vinkler er lik 180 grader,
- Skjæringspunktet mellom diagonaler i en vinkel på 90 grader,
- Halveringslinjene til en rombe er dens diagonaler,
- Ved skjæring deles diagonalen i like deler.

En rombe har følgende egenskaper:

Hvis et parallellogram der diagonalene møtes i en vinkel på 90 grader, kalles det en rombe.
- Hvis et parallellogram hvis halveringslinje er en diagonal, kalles det en rombe.
– Hvis et parallellogram har like sider, er det en rombe.
– Hvis en firkant har like sider, er det en rombe.
- Hvis en firkant der halveringslinjen er en diagonal og diagonalene møtes i en vinkel på 90 grader, så er det en rombe.
– Hvis et parallellogram har samme høyder, er det en rombe.

Fra tegnene ovenfor kan vi konkludere med at de er nødvendige for å lære å skille en rombe fra andre figurer som ligner på den.

For i en rombe er alle sider like omkretsen er i henhold til følgende formel:
P=4a
Område med rombeformel

Det er flere formler. Den enkleste løses ved å legge til arealet av 2 trekanter, som ble oppnådd ved å dele diagonalene.

Ved å bruke den andre formelen kan du løse problemer med kjente diagonaler til en rombe. I dette tilfellet vil arealet av romben være: summen av diagonalene delt på to.

Det er veldig enkelt å løse og vil ikke bli glemt.

Den tredje formelen kan brukes når du kjenner vinkelen mellom sidene. Når du vet det, kan du finne arealet til en rombe, det vil være lik kvadratet på sidene ganger sinusen til vinkelen. Det spiller ingen rolle hvilken vinkel. siden sinusen til en vinkel har samme verdi.

Det er viktig å huske at arealet måles i kvadrater, og omkretsen måles i enheter. Disse formlene er veldig enkle å bruke i praksis.

Du kan også støte på problemer med å finne radiusen til en sirkel innskrevet i en rombe.

Det er også flere formler for dette:

Ved å bruke den første formelen, er radius funnet som produktet av diagonalene delt på tallet oppnådd ved å legge til alle sider. eller lik halve høyden (r=h/2).

Den andre formelen tar prinsippet fra den første og gjelder vi kjenner diagonalene og sidene til en rombe.

I den tredje formelen kommer radiusen fra høyden til den mindre trekanten som kommer fra skjæringspunktet.

Definisjon av en diamant

Rombe er et parallellogram der alle sider er like med hverandre.

Online kalkulator

Hvis sidene på en rombe danner en rett vinkel, får vi torget.

Diagonalene til en rombe skjærer hverandre i rette vinkler.
Diagonalene til en rombe er halveringslinjene til vinklene.

Området til en rombe, som områdene til de fleste geometriske former, kan finnes på flere måter. La oss forstå essensen deres og vurdere eksempler på løsninger.

Formel for området til en rombe ved side og høyde

La oss få en rombe med en side a a en og høyde h h h, trukket til denne siden. Siden en rombe er et parallellogram, finner vi arealet på samme måte som arealet til et parallellogram.

S = a ⋅ h S=a\cdot h S=en ⋅h

A a en- side;
h h h- høyde senket til siden a a en.

La oss løse et enkelt eksempel.

Eksempel

Siden av en rombe er 5 (cm). Høyden senket til denne siden har en lengde på 2 (cm). Finn arealet til en rombe S S S.

Løsning

A = 5 a = 5 a =5
h = 2 h = 2 h =2

Vi bruker formelen vår og regner ut:
S = a ⋅ h = 5 ⋅ 2 = 10 S=a\cdot h=5\cdot 2=10S=en ⋅h =5 ⋅ 2 = 1 0 (se kvm.)

Svar: 10 cm kvm.

Formel for området til en rombe ved hjelp av diagonaler

Alt er like enkelt her. Du trenger bare å ta halve produktet av diagonalene og få området.

S = 1 2 ⋅ d 1 ⋅ d 2 S=\frac(1)(2)\cdot d_1\cdot d_2S=2 1 ​ ⋅ d 1 ​ ⋅ d 2 ​

D 1, d 2 d_1, d_2 d 1 ​ , d 2 ​ - diagonaler av en rombe.

Eksempel

En av diagonalene til en rombe er 7 (cm), og den andre er 2 ganger større enn den første. Finn arealet av figuren.

Løsning

D 1 = 7 d_1 = 7 d 1 ​ = 7
d 2 = 2 ⋅ d 1 d_2=2\cdot d_1d 2 ​ = 2 ⋅ d 1 ​

La oss finne den andre diagonalen:
d 2 = 2 ⋅ d 1 = 2 ⋅ 7 = 14 d_2=2\cdot d_1=2\cdot 7=14d 2 ​ = 2 ⋅ d 1 ​ = 2 ⋅ 7 = 1 4
Deretter området:
S = 1 2 ⋅ 7 ⋅ 14 = 49 S=\frac(1)(2)\cdot7\cdot14=49S=2 1 ​ ⋅ 7 ⋅ 1 4 = 4 9 (se kvm.)

Svar: 49 cm kvm.

Formel for arealet til en rombe ved bruk av to sider og vinkelen mellom dem

S = a 2 ⋅ sin ⁡ (α) S=a^2\cdot\sin(\alpha)S=en 2 ⋅ synd(α)

A a en- siden av romben;
α\alfa α - hvilken som helst vinkel på romben.

Eksempel

Finn arealet til en rombe hvis hver av sidene er 10 cm og vinkelen mellom to tilstøtende sider er 30 grader.

Løsning

A = 10 a = 10 a =1 0
α = 3 0 ∘ \alpha=30^(\circ)α = 3 0 ∘

Ved å bruke formelen får vi:
S = a 2 ⋅ sin ⁡ (α) = 100 ⋅ sin ⁡ (3 0 ∘) = 50 S=a^2\cdot\sin(\alpha)=100\cdot\sin(30^(\circ))= 50S=en 2 ⋅ sin(α) =1 0 0 ⋅ synd (3 0 ∘ ) = 5 0 (se kvm.)

Svar: 50 cm kvm.

Formel for arealet til en rombe basert på radiusen til den innskrevne sirkelen og vinkelen

S = 4 ⋅ r 2 sin ⁡ (α) S=\frac(4\cdot r^2)(\sin(\alpha))S=synd(α)4 ⋅ r 2 ​

R r r- radius av den innskrevne sirkelen i en rombe;
α\alfa α - hvilken som helst vinkel på romben.

Eksempel

Finn arealet til en rombe hvis vinkelen mellom basene er 60 grader og radiusen til den innskrevne sirkelen er 4 (cm).

Løsning

R = 4 r = 4 r =4
α = 6 0 ∘ \alpha=60^(\circ)α = 6 0 ∘

S = 4 ⋅ r 2 sin ⁡ (α) = 4 ⋅ 16 sin ⁡ (6 0 ∘) ≈ 73,9 S=\frac(4\cdot r^2)(\sin(\alpha))=\frac(4\ cdot 16)(\sin(60^(\circ)))\approx73.9S=synd(α)4 ⋅ r 2 ​ = synd (6 0 ∘ ) 4 ⋅ 1 6 ​ ≈ 7 3 . 9 (se kvm.)

Svar: 73,9 cm kvm.

Formel for arealet til en rombe basert på radiusen til den innskrevne sirkelen og siden

S = 2 ⋅ a ⋅ r S=2\cdot a\cdot rS=2 ⋅ en ⋅r

A a en-siden av romben;
r r r- radius av den innskrevne sirkelen i en rombe.

Eksempel

La oss ta betingelsen fra forrige oppgave, men gi oss beskjed i stedet for vinkelen siden av romben lik 5 cm.

Løsning

A = 5 a = 5 a =5
r = 4 r = 4 r =4

S = 2 ⋅ a ⋅ r = 2 ⋅ 5 ⋅ 4 = 40 S=2\cdot a\cdot r=2\cdot5\cdot4=40S=2 ⋅ en ⋅r =2 ⋅ 5 ⋅ 4 = 4 0 (se kvm.)

Svar: 40 cm kvm.